Two coherent sources S1 and S2 are separated by a small distance d. The fringes obtained on the screen will be:
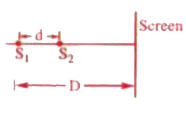
straight lines
semicirles
concentric circles
points
The correct Answer is:C
Step by step video & image solution for Two coherent sources S_(1)" and "S_(2) are separated by a small distance d. The fringes obtained on the screen will be: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -IA (DIFFRACTION)
33 Videos
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -IA (POLARASATION)
29 Videos
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -III (POLARISITION)
10 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
Similar Questions
Two coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View SolutionTwo coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
View SolutionTwo monochromatic coherent point sources S1 and S2 are separated by a distance L. Each sources emits light of wavelength λ, where L>>λ. The line S1S2 when extended meets a screen perpendicular to it at point A. Then
View SolutionConsider two coherent, monochromatic (wavelength λ) sources S1andS2, separated by a distance d. The ratio of intensities of S1 and that of S2 (which is responsible for interference at point P, where detector is located) is 4. The distance of point P from S1 is (if the resultant intensity at point P is equal to 94 times of intensity of S1) (Given : ∠S2S1P=90∘,d>0andn is a positive integer)
View SolutionIn Young's doulbe-slit experiment the separation between two coherent sources S1 and S2 is d and the distance between the source and screen is D. In the interference pattern, it is found that exactly in front of one slit, there occurs a minimum. Then the possible wavelengths used in the experiment are
View SolutionThere is a large circle (not a screen this time) around two coherent
sources S1 and S2 kept at a distance d=3.4λ.
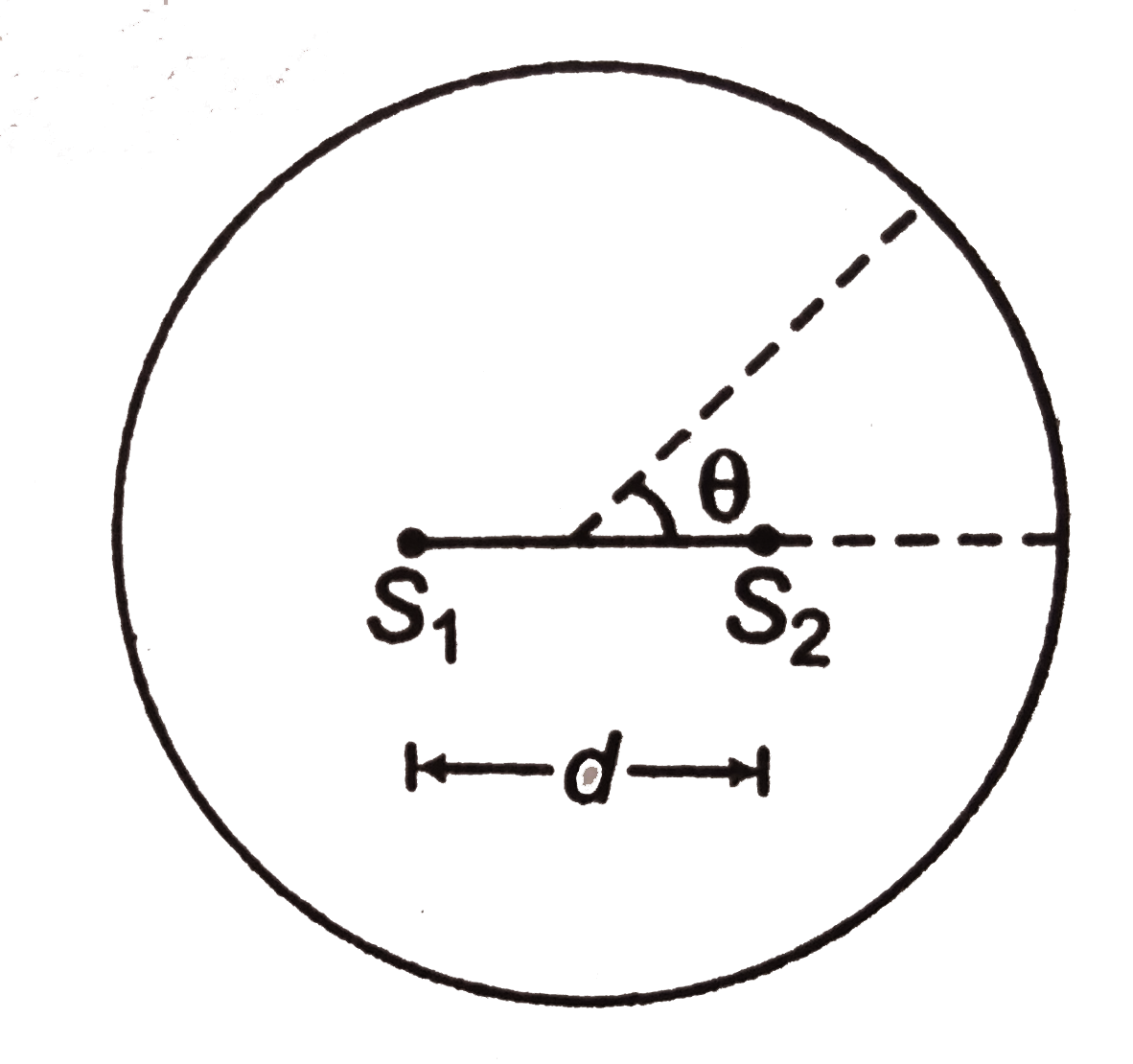
(a) Find total number of maximas on this circle.
(b) Four angular positions corresponding to third order maxima on this circle.
View SolutionTwo coherent source of light can be obtained by
View SolutionStatement I: Two point coherent sources of light S1 and S2 are placed on a line as shown in figure. P and Q are two points on that line. If at point P maximum intensity is observed, then maximum intensity should also be observed at Q.

Statement II: In figure the distance |S1P−S2P| is equal to distance |S1Q−S2Q|.
View SolutionFigure shows two line sources of sound, S1andS2 separated by a distance 4 m.The two sources are in same phase at all times.The source emit same power and their lengths are also same.A detector moves along a circle with center at S2 and radius 3m. The wavelength of the sound is 1m.When it is at A the intensity of sound due to source S2 only is I0.
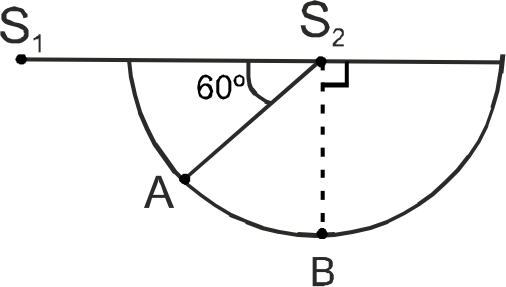
The intensity o sound of B due to S1andS2 is :
View Solution
