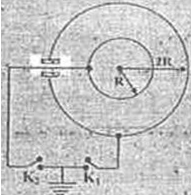
Two concentric shells of radii and are shown in (Fig. 3.115). Initially, a charge q is imparted to the inner shells. Now, key is closed and opened and then key is closed and opened. After the keys are alterbately closed n times each, find the potential difference between the shells. Note that finally key remains closed.
 .
.
The correct Answer is:
When is closed first time, the outer sphere is earthed and the potential on it becomes zero. Let the charge on it be .
Potential due to charge on the inner sphere and that due to charge on the outer sphere is
or
When is closed first time, the potential on the inner sphere becomes zero as it earthed. Let the new charge on the inner sphere be.
or
Now, when will be closed second time, charge on the outer sphere will be , i.e., . After one event involving closure and opening of and , charge is reduced to half of its initial value. Similarly, when will be closed time, charge on the outer sphere will be as each time charge will be reduced to half of the previous value.
After closing time, charge on the inner shell will be negative of half the charge on the outer shell, i.e., and potential on it will be zero. For potential of the outer shell
=
Potential difference is
.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Single Correct
56 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Multiple Correct
10 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.3
9 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
Two concentric shells of radii R and 2R are shown in the figure. Initially a charge q is imparted to the inner shell. After the keys K1&K2 are alternately closed n times each, find the potential difference between the shells.
View SolutionThere are two concentric spherical shell of radii r and 2r. Initially, a charge Q is given to the inner shell and both the switches are open.

If switch S1 is closed and then opened, charge on the outer shell will be
View SolutionThere are two concentric spherical shells of ratii r and 2r. Intially a charge Q is given to the inner shell. Now switch S1is closed and S2 is opned and the process is repeated n times for both the keys altermatively. Find the final potential between the shells.

View SolutionThere are two concentric spherical shell of radii r and 2r. Initially, a charge Q is given to the inner shell and both the switches are open.

Now, S2 is closed and opened. The charge flowing through the swithc S2 in the process is
View SolutionThere are two concentric spherical shell of radii r and 2r. Initially, a charge Q is given to the inner shell and both the switches are open.

The two steps of the above two problems are repeated b times, the potential differences between the shells will be
View SolutionThree concentric conducting shells of radii a, b and c are shown in (Fig. 3.100). Charge on the shell of radius b is Q. If the key K is closed, find the charges on the innermost and outermost shells and the radio of charge densities of the shells. Given that a:b:c=1:2:3.
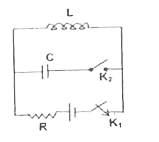
View SolutionShown in the figure is a parallel R , L,C circuit with key K1 closed and K2 opened . When K1 is opened and K2 is closed simultaneously find the maximum potential difference across the capacitor and maximum charge stored in it .
View Solutionthere are two concentric metallic shells of radii R and 2R, if outer shell is given charge q1 , then charge on surface of inner shell will be
View SolutionConsider two concentric metalic shell's of radii R and 2R. The inner shell is having charge Q and outer shell is uncharged. If they are connected with a conducting wire. Then,
View SolutionShown in the figure is an R−L circuit. Just after the key (K) is closed

View Solution
