Two converging glass lenses A and B have focal lengths in the ratio . The radius of curvature of first surface of lens A is 1/4 th of the second surface where as the radius of curvature of first surface of lens B is twice that of second surface. Then the ratio between the radii of the first surfaces of A and B is
The correct Answer is:D
To solve the problem, we need to find the ratio between the radii of the first surfaces of two converging lenses A and B, given their focal lengths and the relationships between their radii of curvature.
1. Identify the Given Information:
- The focal lengths of lenses A and B are in the ratio fA:fB=2:1.
- For lens A, the radius of curvature of the first surface r1A is 14 of the second surface r2A.
- For lens B, the radius of curvature of the first surface r1B is 2 times the second surface r2B.
2. Use the Lens Maker's Formula:
The lens maker's formula is given by:
1f=(μ−1)(1r1+1r2)
where μ is the refractive index of the lens material.
3. Apply the Formula for Lens A:
- Given r1A=14r2A, we can express r2A as 4r1A.
- Substitute into the lens maker's formula:
1fA=(μ−1)(1r1A+14r1A)
=(μ−1)(54r1A)
Thus,
fA=4r1A5(μ−1)
4. Apply the Formula for Lens B:
- Given r1B=2r2B, we can express r2B as 12r1B.
- Substitute into the lens maker's formula:
1fB=(μ−1)(1r1B+2r1B)
=(μ−1)(3r1B)
Thus,
fB=r1B3(μ−1)
5. Set Up the Ratio of Focal Lengths:
We know fAfB=21:
4r1A5(μ−1)r1B3(μ−1)=2
The (μ−1) cancels out:
4r1A5⋅3r1B=2
Rearranging gives:
4r1A⋅3=10r1B
12r1A=10r1B
r1Ar1B=1012=56
6. Conclusion:
The ratio of the radii of the first surfaces of lenses A and B is:
r1Ar1B=56
Final Answer:
The ratio between the radii of the first surfaces of A and B is 56.
- The focal lengths of lenses A and B are in the ratio fA:fB=2:1.
- For lens A, the radius of curvature of the first surface r1A is 14 of the second surface r2A.
- For lens B, the radius of curvature of the first surface r1B is 2 times the second surface r2B.
The lens maker's formula is given by:
1f=(μ−1)(1r1+1r2)
where μ is the refractive index of the lens material.
- Given r1A=14r2A, we can express r2A as 4r1A.
- Substitute into the lens maker's formula:
1fA=(μ−1)(1r1A+14r1A)
=(μ−1)(54r1A)
Thus,
fA=4r1A5(μ−1)
- Given r1B=2r2B, we can express r2B as 12r1B.
- Substitute into the lens maker's formula:
1fB=(μ−1)(1r1B+2r1B)
=(μ−1)(3r1B)
Thus,
fB=r1B3(μ−1)
We know fAfB=21:
4r1A5(μ−1)r1B3(μ−1)=2
The (μ−1) cancels out:
4r1A5⋅3r1B=2
Rearranging gives:
4r1A⋅3=10r1B
12r1A=10r1B
r1Ar1B=1012=56
The ratio of the radii of the first surfaces of lenses A and B is:
r1Ar1B=56
The ratio between the radii of the first surfaces of A and B is 56.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE III LEVEL -II (ADVAMCED) MORE THAN ONE CORRECT TYPE QUESTIONS)
1 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE III LEVEL -II (ADVAMCED) LINKED COMPREHENSION TYPE QUESTIONS)
3 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE III LEVEL -I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
7 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
Similar Questions
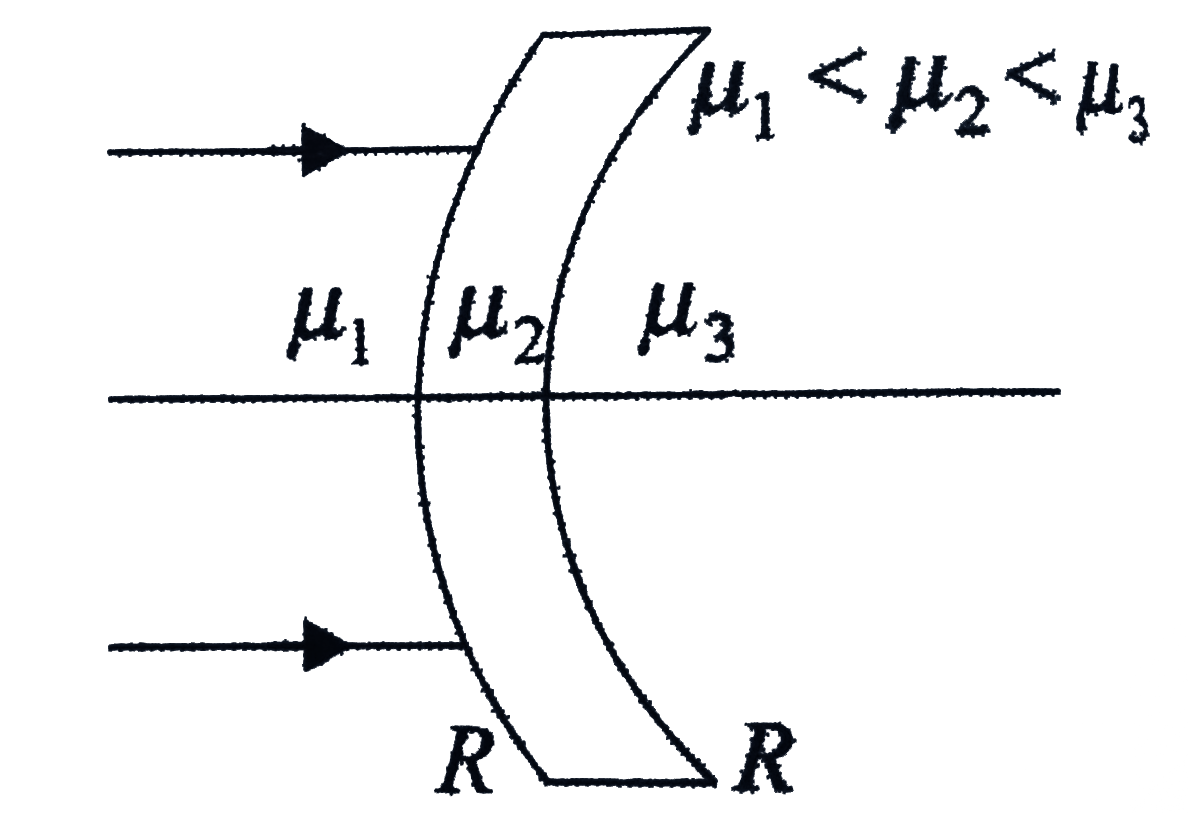
Find the focal length of the lens shown in Fig . The radii of curvature of both the surfaces are equal to R.
View SolutionRadius of curvature of first surface of double convex lens is three times that of the other. If focal length of the lens is 30 cm and refractive index of the lens is 3/2, then radius of curvature of the first surface is
View Solution
Knowledge Check
A biconvex lens has focal length 23 times the radius of curvature of either surface. Calculate refraction index f material of the lens.
A1.75B1.33C1.5D1.0The radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
Aact as a convex lens only for the objects that lie on its curved side.Bact as a concave lens for the objects that lie on its curved side.Cact as a convex lens irrespective of the side on which the object lies.Dact as a concave lens irrespective of side on which the object lies.
A convex-concave diverging lens is made of glass of refractive index 1.5 and focal length 24 cm. radius of curvature for one surface is double that of the other. Then radii of curvature for the two surfaces are (in cm )
View SolutionThe convex surface of a plano-convex lens is silvered and the radius of curvature of this surface is R. Find the focal length of the system:
View SolutionA biconvex lens has focal length 23 times the radius of curvature of either surface. Calculate refraction index f material of the lens.
View SolutionA plano convex lens is made of glass of refractive index 1.5. The radius of curvature of its convex surface is R. Its focal length is
View SolutionA double convex lens has focal length 25 cm. The radius of curvature of one of the surfaces is double of the other. Find the radii, if the refractive index of the material of the lens is 1.5.
View SolutionTwo blocks A and B of the same mass and surface finish are sliding on the same surface. Area of contact of A is twice that of the B. The frictional force between A and the surface is
View Solution
