Question

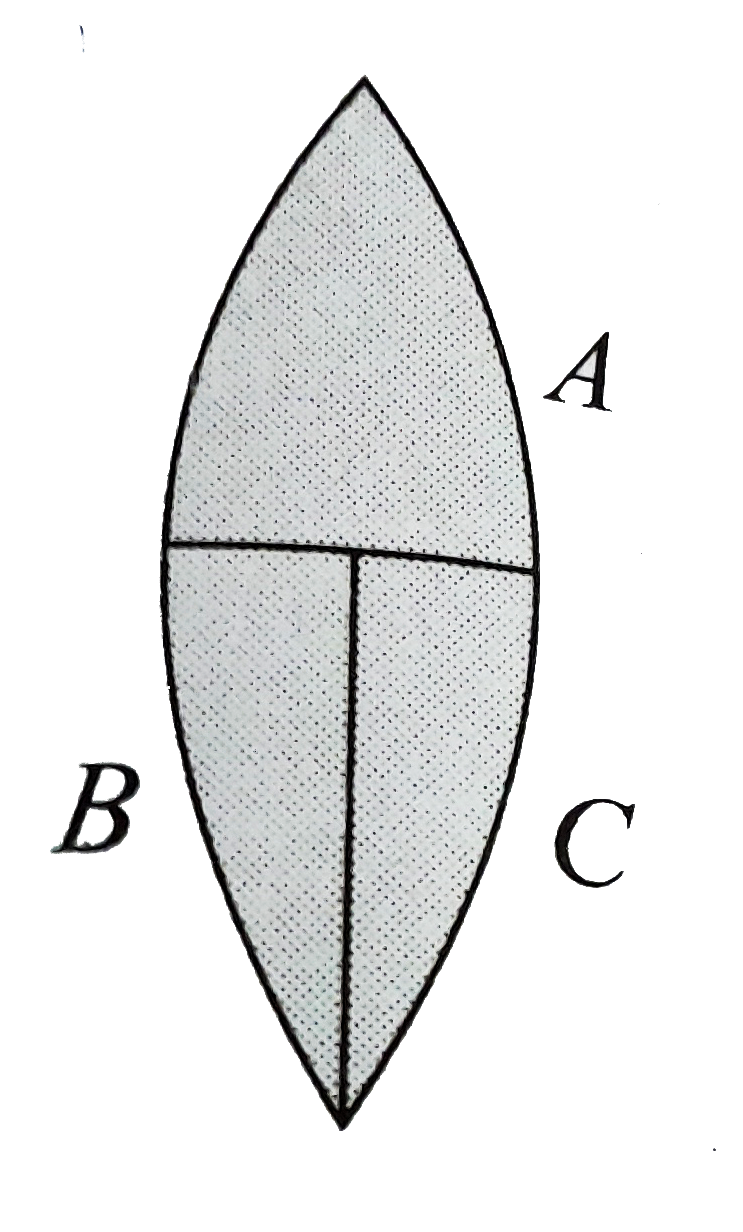
A thin double convex lens is cut into two equal pieces A and B by a plane containing principal axis. The piece B is further cut into two more pieces pieces C and D by another plane perpendicular to the principal axis. If the focal power of the original lens is P, then thos of A and C are

Options

A. `P,P/4`
B. `P,P/2`
C. `P/2,2P`
D. `P/2,P/4`

Answer

B

Explanation

To solve the problem, we need to determine the focal powers of the pieces A and C after the lens is cut. Let's break it down step by step.

Step 1: Understanding the Original Lens
The original lens is a thin double convex lens with a focal power \( P \). The focal power \( P \) is given by the formula:
\( P = \frac{1}{f} = (n - 1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right) \)
where \( n \) is the refractive index of the lens material, and \( R_1 \) and \( R_2 \) are the radii of curvature of the two surfaces of the lens.

Step 2: Cutting the Lens into Two Pieces A and B
When the lens is cut into two equal pieces A and B along a plane containing the principal axis, the focal power of piece A remains the same as that of the original lens because the curvature of the surfaces does not change. Thus, the focal power of piece A is:
\( P_A = P \)

Step 3: Further Cutting Piece B into Pieces C and D
Next, piece B is cut into two more pieces C and D by a plane perpendicular to the principal axis. This means that piece C will have one curved surface (with radius \( R_1 \)) and the other surface will be flat (with radius approaching infinity).

Step 4: Calculating the Focal Power of Piece C
For piece C, the focal power can be calculated using the formula for a lens with one flat surface:
\( P_C = \frac{1}{f_C} = (n - 1) \left( \frac{1}{R_1} - 0 \right) = (n - 1) \frac{1}{R_1} \)
Since the original lens had a focal power of \( P = (n - 1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right) \), and since piece C only has one curved surface, we can relate the focal power of piece C to the original focal power:
\( P_C = \frac{P}{2} \)

Final Results
Thus, we find the focal powers of the pieces:
- For piece A: \( P_A = P \)
- For piece C: \( P_C = \frac{P}{2} \)

Summary of the Solution
- The focal power of piece A is \( P \).
- The focal power of piece C is \( \frac{P}{2} \).