Two converging lenses of unequal focal lengths can be used to reduce the aperture of a parallel beam of light without loosing the energy of the light. This increases the intensity. Describe how the converging lenses should be placed to do this.
To solve the problem of how to arrange two converging lenses of unequal focal lengths to reduce the aperture of a parallel beam of light without losing energy and thus increasing intensity, we can follow these steps:
1. Identify the Lenses: Let’s denote the two converging lenses as L1 and L2, with focal lengths f1 and f2 respectively.
2. Understanding the Arrangement: To achieve the desired effect, we need to place the lenses in a specific configuration. The key is to position the second lens (L2) within the focal range of the first lens (L1).
3. Positioning the Lenses: Place lens L1 such that it faces the incoming parallel beam of light. The parallel rays of light will converge after passing through L1 and will focus at its focal point, which is at a distance f1 from L1.
4. Placing the Second Lens: Now, place lens L2 at a distance less than f1 from lens L1. This means that L2 should be positioned within the focal length of L1.
5. Light Path: As the parallel rays of light pass through L1, they will converge towards the focal point of L1. However, since L2 is placed within this focal range, the rays will then encounter lens L2.
6. Refraction through L2: The rays will be refracted again by lens L2. Since L2 is a converging lens, it will further converge the rays, but because it is positioned within the focal range of L1, it will effectively reduce the aperture of the beam of light.
7. Resulting Beam: The output will be a narrower beam of light that has been intensified due to the reduced aperture while maintaining the energy of the light, thus increasing the intensity.
Final Arrangement:
- Lens L1 is positioned to face the incoming parallel beam.
- Lens L2 is placed within the focal length of L1.
- Lens L1 is positioned to face the incoming parallel beam.
- Lens L2 is placed within the focal length of L1.
Topper's Solved these Questions
Similar Questions
Two converging lenses of focal lengths f1=10cm and f2=20cm are placed at some separation. A parallel beam of light is incident on first lens. Then,
View SolutionIn the figure shown a converging lens and a diverging lens of focal lengths 20cm and -5cm respectively are separated by a distance such that a paralel beam of light of intensity 100 wa/m2 incident on the converging lens comes out as parallel beam from the diverging lens. Find the intensity of the outgoing beam in wa/m2
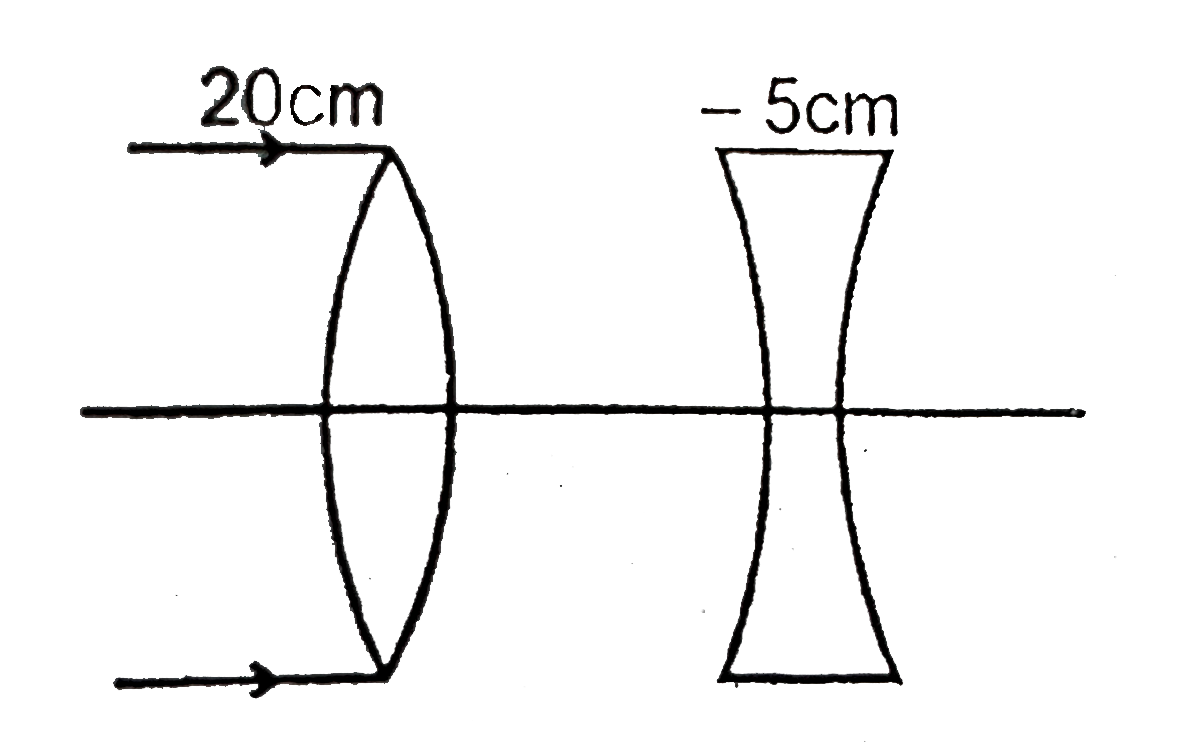
View SolutionA convex lens of focal length 1.0m and a concave lens of focal length 0.25m are 0.75m apart. A parallel beam of light is incident on the convex lens. The beam emerging after refraction from both lenses is
View SolutionA convex lens of focal length 100 cm and a concave lens of focal length 10 cm are placed coaxialiy at a separation of 90 cm. If a parallel beam of light is incident on convex lens, then after passing through the two lenses the beam
View SolutionA perfectly reflecting solid hemisphere of radius R is placed in the path of a parallel beam of light of large aperture. If the beam carrries an intensity l, find the force exerted by the beam on the hemisphere.
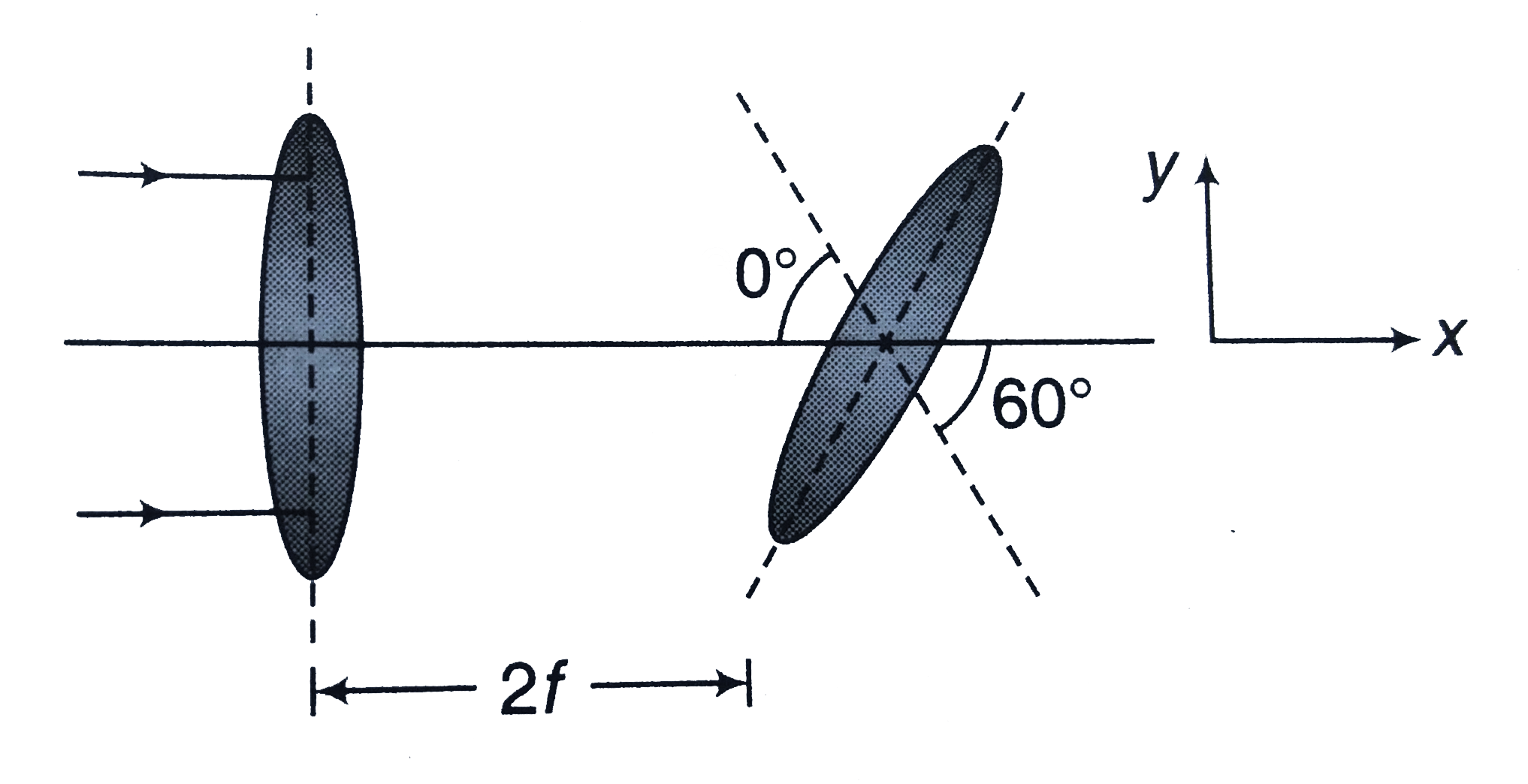
View SolutionTwo converging lenses of the same focal length f are separated by a distance 2f. The axis of the second lens is inclined at angle θ=60∘ with respect to the axis of the first lens. A parallel paraxial beam of light is incident from left side of the lens. Find the coordinates of the final image with respect to the origin of the first lens.
View SolutionConsider a 'beam expander' which consists of two converging lenses of focal length 40 cm and 100 cm having a common optical axis. A laser beam of diameter 4 mm is incident on the 40 cm focal length lens. Then what is the diameter of the final beam (see figure)
_E01_142_Q01.png)
View SolutionTwo converging glass lenses A and B have focal lengths in the ratio 2:1. The radius of curvature of first surface of lens A is 1/4 th of the second surface where as the radius of curvature of first surface of lens B is twice that of second surface. Then the ratio between the radii of the first surfaces of A and B is
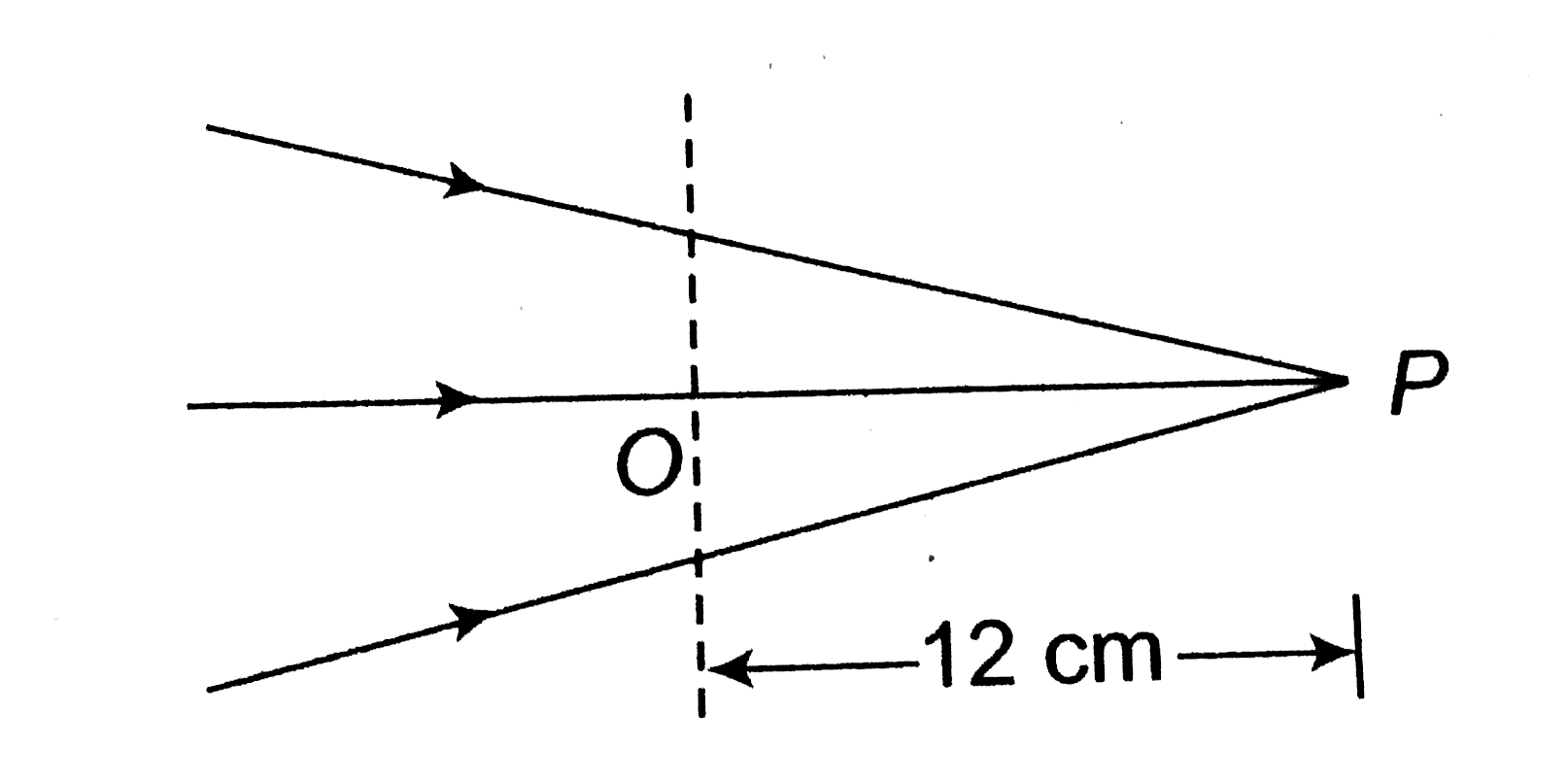
View SolutionFigure given below shows a beam of light converging at point P. When a concave lens of focal length 16cm is introduced in the path of the beam at a place O shown by dotted line such that OP becomes the axis of the lens, the beam converges at a distance x from the lens. The value x will be equal to
View SolutionL is a lens such that a parallel beam of light I ncident on it, after refraction, converges to a point at a distance x from it and M is a mirror such that a parallel lbeam of light incident on it, after reflection, converges to a point at a distance y from it. Now the lens L and mirror M are placed at a distan 2(x+y) from each other. An object of size 2 cm is kept infront of lens at a distance 2x from it. Find the nature, position , and size of the image that willl be seen by an observer looking toward the mirror through the lens.
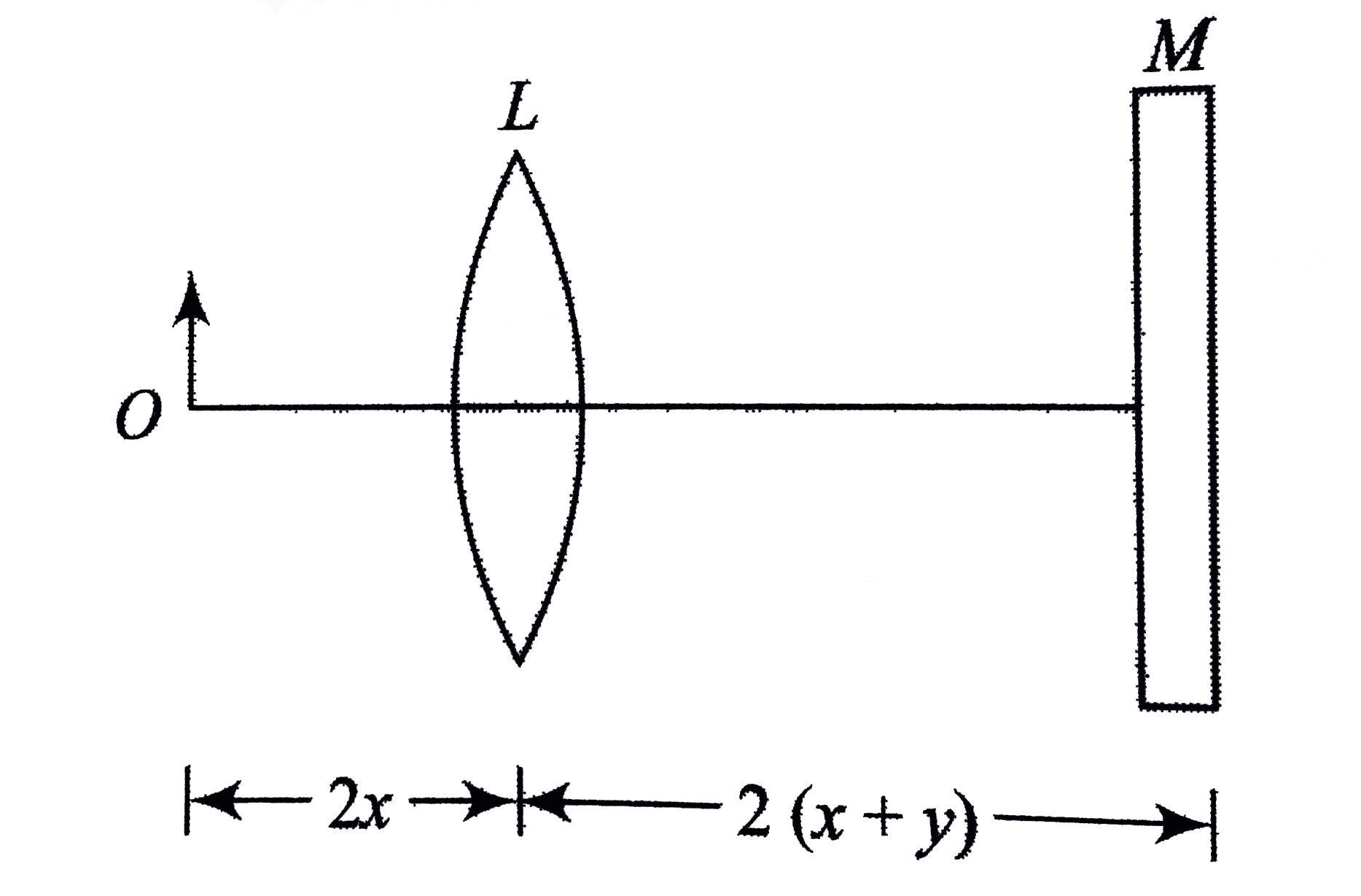
View Solution
