Two different metal rods of equal lengths and equal areas of cross-section have their ends kept at the same temperature θ1 and θ2. if K1 and K2 are their thermal conductivities, ρ1 and ρ2 their densities and S1 and S2 their specific heats, then the rate of flow of heat in the two rods will be the same if:
k1k2=ρ1s1ρ1s2
k1k2=ρ1s2ρ2s1
k1k2=θ1θ2
k1=k2
The correct Answer is:D
To solve the problem of determining the condition under which the rate of heat flow through two different metal rods is the same, we can follow these steps:
1. Understand the Setup: We have two metal rods (Rod 1 and Rod 2) of equal lengths (L) and equal cross-sectional areas (A). The ends of both rods are maintained at the same temperatures, θ1 and θ2.
2. Use the Heat Transfer Formula: The rate of heat transfer (dq/dt) through a rod can be expressed using Fourier's law of heat conduction:
dqdt=−k⋅A⋅ΔTL
where:
- k is the thermal conductivity,
- A is the cross-sectional area,
- ΔT is the temperature difference (θ2 - θ1),
- L is the length of the rod.
3. Write the Heat Transfer Equations for Both Rods:
- For Rod 1:
dq1dt=−k1⋅A⋅θ2−θ1L
- For Rod 2:
dq2dt=−k2⋅A⋅θ2−θ1L
4. Set the Heat Transfer Rates Equal: Since we want the rate of heat flow in both rods to be the same, we set the two equations equal to each other:
−k1⋅A⋅θ2−θ1L=−k2⋅A⋅θ2−θ1L
5. Cancel Common Factors: Since the area (A) and the temperature difference (θ2 - θ1) are the same for both rods, we can cancel these terms from both sides of the equation:
k1=k2
6. Conclusion: The rate of flow of heat in the two rods will be the same if their thermal conductivities are equal:
k1=k2
dqdt=−k⋅A⋅ΔTL
where:
- k is the thermal conductivity,
- A is the cross-sectional area,
- ΔT is the temperature difference (θ2 - θ1),
- L is the length of the rod.
- For Rod 1:
dq1dt=−k1⋅A⋅θ2−θ1L
- For Rod 2:
dq2dt=−k2⋅A⋅θ2−θ1L
−k1⋅A⋅θ2−θ1L=−k2⋅A⋅θ2−θ1L
k1=k2
k1=k2
Topper's Solved these Questions
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Advance MCQs with One or More Option Correct
20 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Unsolved Numerical Problems for Preparation of NSEP,INPhO&IPhO
66 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Conceptual MCQs Single Option Correct
24 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
82 Videos
- Kinetic Theory of Gases and Gas LawsBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO
64 Videos
Similar Questions
Two rods of same length and area of cross-section A1 andA2 have their ends at the same temperature. If K1andK2 are their thermal conductivities, c1andc2 are their specific heats and d1and d2 are their densities, then the rate of flow of heat is the same in both the rods if
View SolutionIn the following situations, the length and area of cross-section of each rod is same. Find temperature θ at junction of rods.
(a)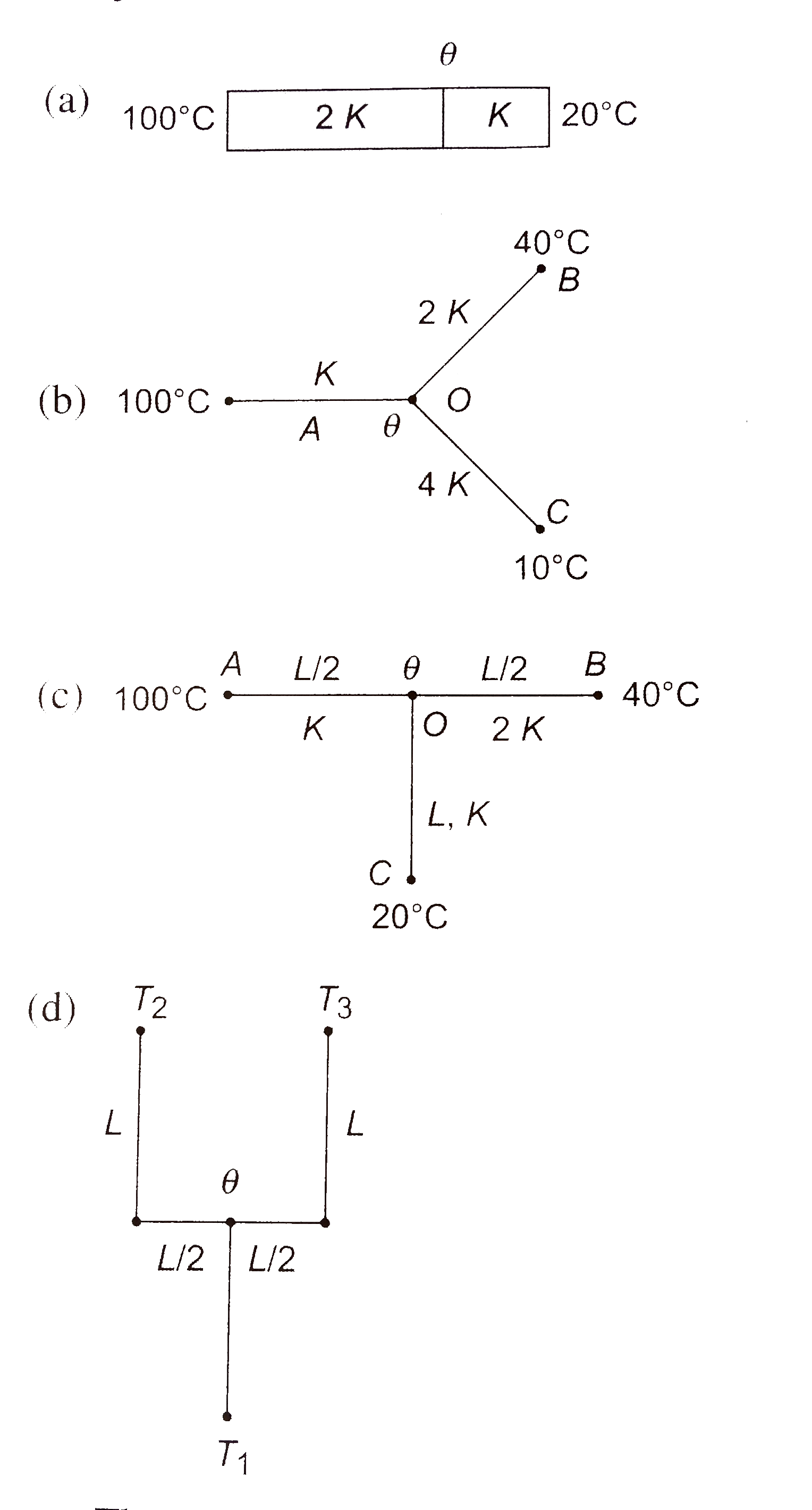
(b)
(c )
(d)
The thermal conductivity of each rod is K.
View Solution
Knowledge Check
Two different metal rods of the same length have their ends kept at the same temperature θ1, and θ2with θ2>θ1. If A1 and A2 are their cross-sectional areas and K1 and K2 their thermal conductivities, the rate of flow of heat in the two rods will be the same it:
AA1A2=k1k2BA1A2=k2k1CA1A2=k1θ1k2θ2DA1A2=k2θ2k1θ1Two rods of same length and areas of cross section A1 and A2 have their ends at same temperature. If K1 and K2 are their thermal conductivities, C1 and C2 their specific heats and ρ1 and ρ2 are their densities, then the condition that rate of flow of heat is same in both the rods is
AA1/A2=K1/K2BA1/A2=K1C1ρ1/K2C2ρ2CA1/A2=K2C1ρ1/K1C2ρ2DA1/A2=K2/K1Two rods of the same length and areas of cross-section A1 and A2 have their ends at the same temperature. K1 and K2 are the thermal conductivities of the two rods. The rate of flow of heat is same in both the rods if-
AA1A2=L1K2BA1A2=K2K1CA1A2=K1K2Dplaced in hot oil
Two metal rods 1 and 2 of same lengths have same temperature difference between their ends. Their thermal conductivities are K1 and K2 and cross sectional areas A1 and A2 respectively. If the rate of heat conduction in 1 is four times that in 2, then
View SolutionTwo rods are connected as shown. The rods are of same length and same cross sectional area. In steady state, the temperature (θ) of the interface will be -
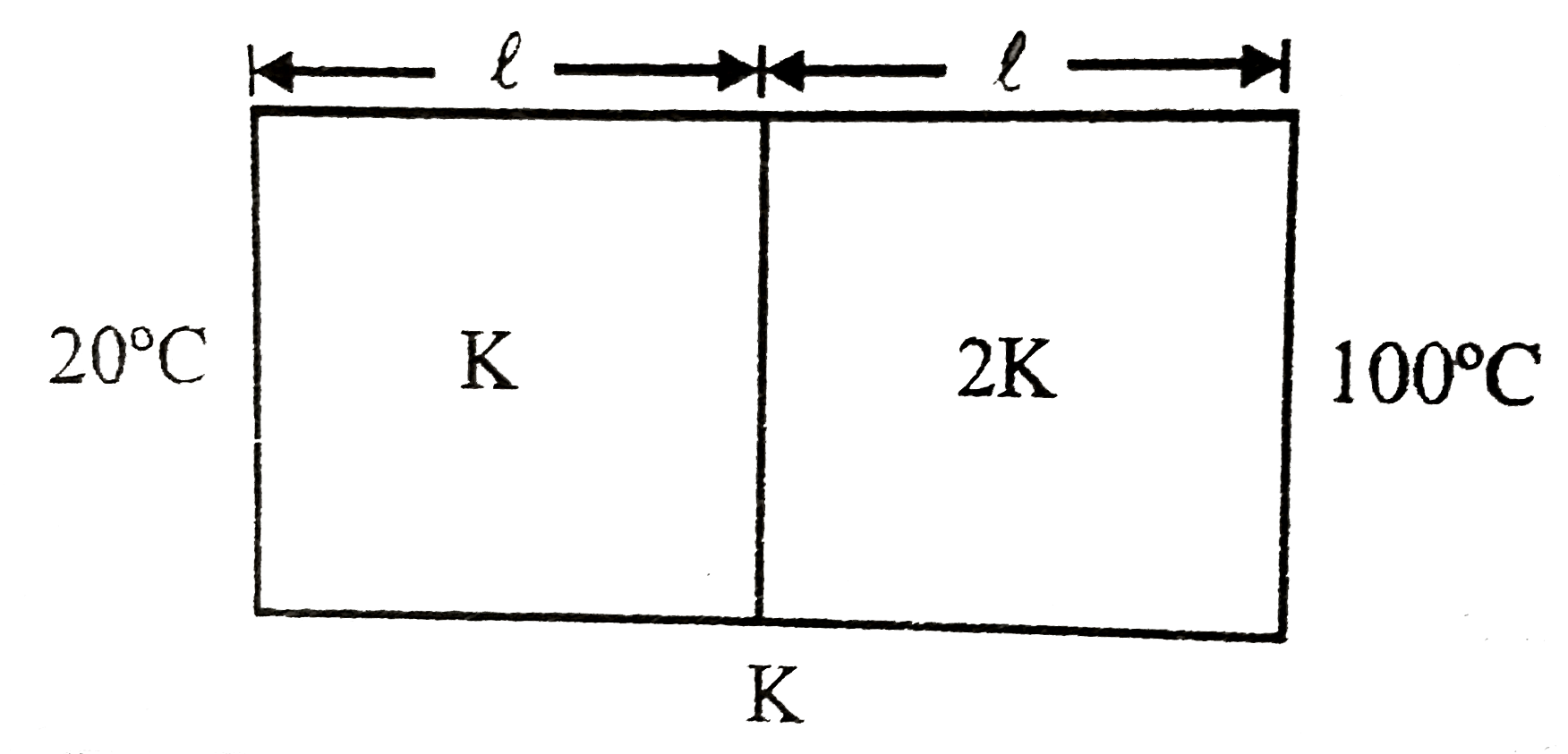
View SolutionTwo rods A and B are of equal lengths. Their ends of kept between the same temperature and their area of cross-section are A1 and A2 and thermal conductivities K1 and K2. The rate of heat transmission in the two rods will be equal, if
View SolutionOne end of thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two section of length l1 and l2 thermal conductivities k1 and k2 respectively. The temerature at the interface of two section is
View SolutionTwo cylindrical rods of lengths l1 and l2, radii r1 and r2 have thermal conductivities k1 and k2 respectively. The ends of the rods are maintained at the same temperature difference. If l1=2l2 and r1=r2/2, the rates of heat flow in them will be the same if k1/k2 is:
View Solution
