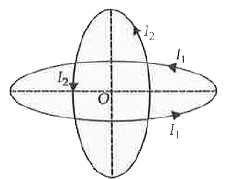
Two flat circular coils have a common centre, but their planes are at right angles to each other. The inner coil has 150 turns and radius of 2π a cm. The outer coil has 400 turns and a radius of 21 cm. The magnitude of the resultant magnetic field at the common centres of the coils when a current of 200 mA is sent through each of them is

A

10−3Wbm−2

B

2×10−3Wbm−2

C

5×10−3Wbm−2

D

7×10−3Wbm−2

Text Solution
Verified by Experts

The correct Answer is:A

For coil 1 (In horizontal plane)
N1=150,R1=πcm=π×10−2m
I1=200mA=200×10−3A
For coil 2(In vertical plane)
N2=400,R2πcm=2π×10−2m
I2=200mA=200×10−3A
Magnetic field at the common centre O due to current in coil 1 is
B1=μ04πN1I12πR1=μ0N1I12R1
Magnetic field at O due to current in coil 2 is
B2=μ04πN2I22πR2=μ0N2I22R2
Resultant magnetic field at O is
B=√B21+B22 (∵B1is⊥toB2)
Substututing the given values , we get
B=        ⎷(μ0×150×200×10−32×π×10−2)2+(μ0×400×200×10−32×2π×10−2)2
μ0×200×10−3×102×π×10−2√(15)2+(20)2=10−3Wbm−2
ocr_image

Doubtnut Promotions Banner
|
Class 12PHYSICSMOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The magnitude of the magnetic field at the centre of the tightly wound 150 turn coil of radius 12 cm carrying a current of 2 A is

    A18G
    B19.7G
    C15.7G
    D17.7G

  • The magnitude of the magnetic field at the centre of the tightly wound 150 turn coil of radius 12 cm carrying a current of 2 A is

    A18G
    B19.7G
    C15.7G
    D17.7G

  • Two identical coils have a common centre and their planes are at right angles to each other. They carry equal currents. If the magnitude of the magnetic field at the centre due to one of the coils is B then that due to the combination is

    AB
    B√2B
    CB√2
    D2B