Two forces →F1=500N due east and →F2=250N due north have their common initial point. →F2−→F1 is
250√5N,tan−1(2)WofN
250N,tan−1(2)W of N
Zero
750N,tan−1(3/4)NofW
The correct Answer is:A
To solve the problem of finding the vector difference →F2−→F1, we will follow these steps:
Step 1: Identify the Forces
We have two forces:
- →F1=500N due east
- →F2=250N due north
Step 2: Represent the Forces as Vectors
We can represent these forces in vector form using Cartesian coordinates:
- →F1=500^i (where ^i represents the east direction)
- →F2=250^j (where ^j represents the north direction)
Step 3: Calculate the Vector Difference
To find →F2−→F1:
→F2−→F1=250^j−500^i
This can be expressed as:
→F2−→F1=−500^i+250^j
Step 4: Find the Magnitude of the Resultant Vector
To find the magnitude of the resultant vector →R=−500^i+250^j, we use the Pythagorean theorem:
|→R|=√(−500)2+(250)2
Calculating the squares:
|→R|=√250000+62500=√312500
|→R|=250√5N
Step 5: Determine the Direction of the Resultant Vector
To find the angle θ that →R makes with the negative x-axis (east direction), we can use the tangent function:
tanθ=|opposite||adjacent|=250500=12
Thus,
θ=tan−1(0.5)
Step 6: Final Result
The vector →F2−→F1 has a magnitude of 250√5N and makes an angle θ=tan−1(0.5) with the negative x-axis (east direction).
We have two forces:
- →F1=500N due east
- →F2=250N due north
We can represent these forces in vector form using Cartesian coordinates:
- →F1=500^i (where ^i represents the east direction)
- →F2=250^j (where ^j represents the north direction)
To find →F2−→F1:
→F2−→F1=250^j−500^i
This can be expressed as:
→F2−→F1=−500^i+250^j
To find the magnitude of the resultant vector →R=−500^i+250^j, we use the Pythagorean theorem:
|→R|=√(−500)2+(250)2
Calculating the squares:
|→R|=√250000+62500=√312500
|→R|=250√5N
To find the angle θ that →R makes with the negative x-axis (east direction), we can use the tangent function:
tanθ=|opposite||adjacent|=250500=12
Thus,
θ=tan−1(0.5)
The vector →F2−→F1 has a magnitude of 250√5N and makes an angle θ=tan−1(0.5) with the negative x-axis (east direction).
Topper's Solved these Questions
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Subjective
28 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
Similar Questions
If three forces −→F1,+−→F2and−→F3 are represented by three sides of a triangle and −→F1+−→F2=−−→F3 , then these three forces are concurrent forces and satisfy the condition for equilibrium .
Statement II : A triangle made up of three forces →F1,→F2and→F3 as sides taken in the same order ,satisfy the condition for translatory equilibrium . In the light of the above statements ,choose the most appropriate answer from the options given below :
View SolutionWhich of the figure's six arrangements correctly show the vector addition of forces →F1 and →F2 to yield the third vector, which is meant to represent their net force →Fnet ?

View Solution
Knowledge Check
Two forces −→F1and−→F2 are acting at right angles to each other , find their resultant ?
A√F21−F22B√F21+F22C√(F1+F2)DF1+F2STATEMENT -1 : Net force on a particle w.r.t an inertial frame does notdepend on the velocity of the intertial frame. ,
STATEMENT - 2 : If net force on A is →FA and net force on B is →FB then force on A w.r.t B is (ven(F)A−→FB) .
STATEMENT - 2 : If acceleration of A is →aA and acceleration of B is →aB then, the acceleration of A w.r.t B is (→aA−→aB)AF T FBT F TCT T FDF T TA body placed in free space, is simultaneously acted upon by three forces −→F1,−→F2 and −→F3. The body is in equilibrium and the forces −→F1 and −→F2 are known ot be 36 N due north and 27 N due east respectively. Which of the following best describes the force −→F3?
A36N due southB53N due 60∘ south of eastC45N due 53∘ south of westD45N due 37∘ north of west.
Two forces →F1=3ˆi+4ˆj and →F2=3ˆj+4ˆk are acting simultaneously at a point. What is the magnitude of the resultant force ?
View SolutionA particle of m=5kg is momentarily at rest at x=att=. It is acted upon by two forces →F1 and →F2. Vec(F)1=70ˆj N. The direction and manitude of →F2 are unknown. The particle experiences a constant acceleration, →a,in the direction as shown in (figure) Neglect gravity.
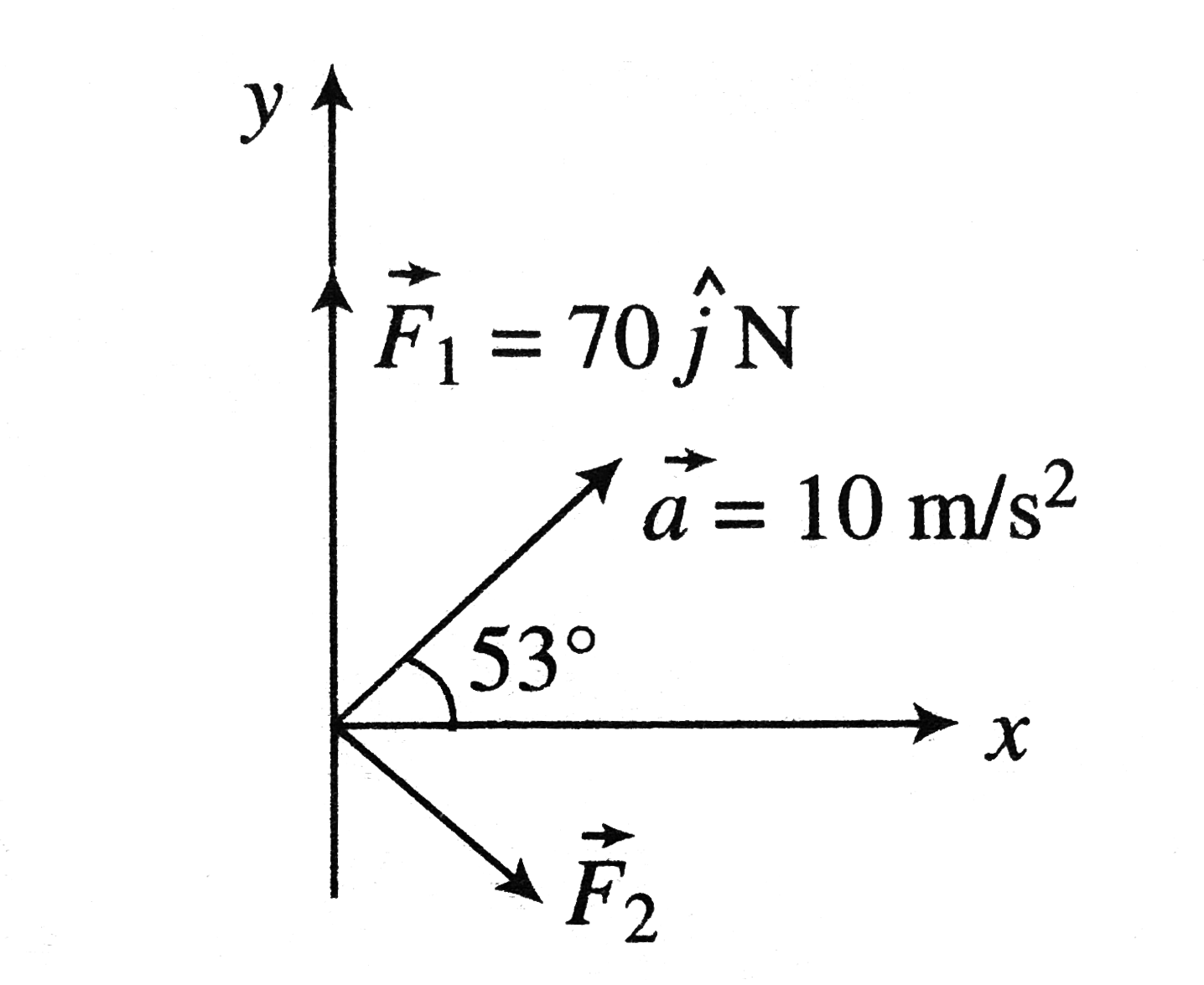
a.Find the missing force →F2.
b. What is the velocity vector of the particle at t=10s?
c. What third force, →F3 is required to make the acceleration of the particle zero? Either give magnitude and direction of →F3 or its components.
View SolutionA slab is subjected to two forces →F1and→F2 of same magnitude F as shown in the figure . Force →F2 is in XY-plane while force F1 acts along z-axis at the point (2→I+3→j) .The moment of these forces about point O will be :

View SolutionFind magnitude and direction of →F2−→F1 if →F1=500N due east and →F2=250N due north:
View SolutionA body of mass m has an initial speed v is acted by two forces →F1 and →F2. After something work done by →F1 is −12mv2 and speed of the body is 2v. Then, the work done by →F2 is
View Solution
