Two identical blocks A and B each of mass 2kg are hanging stationary by a light inextensible flexible string, passing over a light and frictionless pulley, as shown in Fig. A shell C of mass 1kg moving vertically upwards with velocity 9m/s collides with block B and gets stuck to it.

Calculate the time after which block B starts moving downwards.
0.90s
1s
0.60s
0.30s
The correct Answer is:A
When C strikes with B, the combined body starts to rise vertically upward. According to law of conservation of momentum, velocity v0 of combined body (just after collision) is given by
(2+1)v0=1×9 or v0=3m/s
But A is at rest. Therefore, string becomes slack and bodies move under gravity, combined body upwards and A downwards till string again becomes taut. This happens when downward displacement of A becomes equal to upward displacement of combined body. Let it happen at instant t1. Then,
12gt21=3t1−12gt21
or t1=0.3s Displacement of each block at that instant,
h1=12gt210.45m
And velocity of combined body is 3−gt1=0 and velocity of A is gt1=3m/s (downward).
Since at this instant, velocities are different, therefore an impulse is developed in the string and magnitude of velocities of bodies becomes equal. Let that velocity magnitude be v and impulse developed be J. This impulse acts upwards on both the bodies.
Hence for A
2×3−J=v’………i
and for combined body,
J=3v’…………..ii
From above equations
v’=1.2m/s
Now combined body starts to move upwards with velocity v’=1.2m/s and retardation a, where
a=3−23+2=2m/s2
Combined body comes to an instantaneous rest after time
t2=v′a=0.6s
After this instant, combined body starts moving down. Time interval between this instant and instant of collision is given by
t1+t2=0.3+0.6=0.9s
Further height ascended by combined body during time t2 is
h2=v’v2−12at22=0.36m
Maximum height raised by combined body is
h=h1+h2=0.81m
Loss of energy during collision of B and C is
E1=12×1×92−123v20=27J
Loss of energy when impulse is developed in string is
E2=12×2x32−12(2+3)3v20(2+3)(v’)2=5.4J
Loss of mechanical energy till B reaches highest point is
E=E1+E2=27+5.4=32.4J
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Integer
16 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Two identical blocks A and B each of mass 2kg are hanging stationary by a light inextensible flexible string, passing over a light and frictionless pulley, as shown in Fig. A shell C of mass 1kg moving vertically upwards with velocity 9m/s collides with block B and gets stuck to it.

The maximum height reached by B
View SolutionTwo identical blocks A and B each of mass 2kg are hanging stationary by a light inextensible flexible string, passing over a light and frictionless pulley, as shown in Fig. A shell C of mass 1kg moving vertically upwards with velocity 9m/s collides with block B and gets stuck to it.

The loss of mechanical energy up to that instant is
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
Three equal weight A,B and C of mass 2kg each are hanging on a string passing over a fixed frictionless pulley as shown in the figure. The tension in the string connecting weights B and C is approximately

View SolutionTwo masses 2 kg and 4 kg are connected at two ends of light inextensible string passing over a frictionless pulley . If the masses are released , then find the accelaration of the masses and the tension in the string .
View SolutionTwo blocks of masses m and 3m are connected by an inextensible string and the string passes over a fixed pulley which is massless and frictionless. A bullet of mass m moving with a velocity 'u' hits the hanging block of mass 'm' and gets exbedded in it. Find the height through which block A rises after the collision.
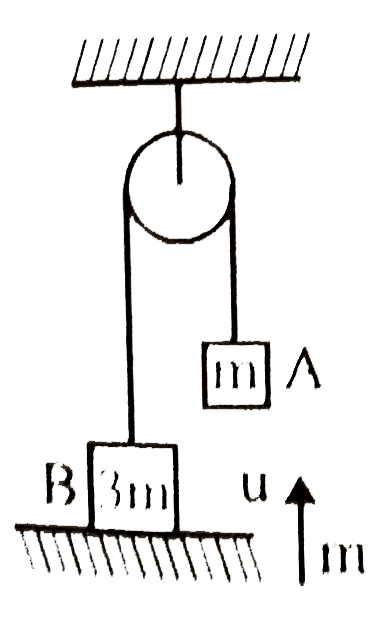
View SolutionA system of two blocks A and B are connected by an inextensible massless string as shown in Fig. The pulley is massless and frictionless. Initially, the system is at rest. A bullet of mass m moving with a velocity u as shown hits block If and gets embedded into it. The impulse imparted by tension force to the block of mass 3m is

View SolutionTwo unequal masses of 1kg and 2kg are connected by an inextensible light string passing over a smooth pulley as shown in figure. A force F=20N is applied on 1kg block find the acceleration of either block (g=10m/s2).

View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionA block of mass 5 kg resting on a horizontal surface is connected by a cord, passing over a light frictionless pulley to a hanging block of mass 5 kg. The coefficient of kinetic friction between the block and surface is 0.5. Tension in the cord is (take, g=9.8ms−2)

View Solution
