Two identical capacitors A and B are charged to the same potential and then made to discharge through resistances RA and RB respectively, with RA>RB.
A will require greater time than B to discharge
More heat will be produced in A than in B.
More heat will be produced in B than in A.
A will require less time than B to discharge completely
The correct Answer is:A
To solve the problem, let's analyze the situation step by step.
Step 1: Understand the scenario
We have two identical capacitors, A and B, which are charged to the same potential. They are then discharged through resistances RA and RB respectively, where RA>RB.
Step 2: Determine the time constant for each capacitor
The time constant τ for a capacitor discharging through a resistor is given by the formula:
τ=R⋅C
where R is the resistance and C is the capacitance of the capacitor. Since both capacitors are identical, they have the same capacitance C.
For capacitor A:
τA=RA⋅C
For capacitor B:
τB=RB⋅C
Step 3: Compare the time constants
Since RA>RB, it follows that:
τA>τB
This means that capacitor A will take longer to discharge compared to capacitor B.
Step 4: Analyze the heat produced
The energy stored in a capacitor is given by:
E=12CV2
Since both capacitors are charged to the same potential V and have the same capacitance C, the energy stored in both capacitors is the same.
When the capacitors discharge, the energy is converted into heat. Therefore, the heat produced in both capacitors will also be the same.
Step 5: Conclusion
Based on the analysis:
1. Capacitor A will require more time to discharge than capacitor B.
2. The heat produced in both capacitors will be the same.
Final Answers:
- A will require greater time than B to discharge (Correct).
- More heat will be produced in A than in B (Incorrect).
- More heat will be produced in B than in A (Incorrect).
- A will require less time than B to discharge completely (Incorrect).
We have two identical capacitors, A and B, which are charged to the same potential. They are then discharged through resistances RA and RB respectively, where RA>RB.
The time constant τ for a capacitor discharging through a resistor is given by the formula:
τ=R⋅C
where R is the resistance and C is the capacitance of the capacitor. Since both capacitors are identical, they have the same capacitance C.
τA=RA⋅C
For capacitor B:
τB=RB⋅C
Since RA>RB, it follows that:
τA>τB
This means that capacitor A will take longer to discharge compared to capacitor B.
The energy stored in a capacitor is given by:
E=12CV2
Since both capacitors are charged to the same potential V and have the same capacitance C, the energy stored in both capacitors is the same.
Based on the analysis:
1. Capacitor A will require more time to discharge than capacitor B.
2. The heat produced in both capacitors will be the same.
- A will require greater time than B to discharge (Correct).
- More heat will be produced in A than in B (Incorrect).
- More heat will be produced in B than in A (Incorrect).
- A will require less time than B to discharge completely (Incorrect).
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IB18videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-II32videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Additional Exercise11videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)26videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II22videos
ELECTROMAGNETIC WAVES
Similar Questions
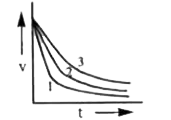
Three identical capacitors A, B and C are charged to the same potential and then made to discharge through three resistances RA,RB and RC, where RA>RB>RC . Their potential differences (V) are plotted against time t, giving the curves 1, 2 and 3. Find the correlations between A, B, C and 1, 2, 3.
 View Solution
View SolutionA capacitor is charged to a certain potential and then allowed to discharge through a resistance R. The ratio of charge on the capacitor to current in the circuit
View SolutionThree identical capacitors are charged by connecting them in parallel across a battery of V volt. They are then allowed to discharge via resistor R1,R2 and R3. Here, Q charge versus t time graphs are shown. Then,
 View Solution
View SolutionA capacitor of capacitance C, charged to a potential difference V, is discharged through a series combination of two resistors R1 and R2. Find the heat generated in resistor R1 during discharging.
View SolutionTwo electric bulbs , rated for the same voltage , have powers of 200Wand100W, respectively. If their resistances are r1andr2 , respectively , then
View SolutionTwo resistors A and B have resistances RAandRBrespectively with RA<RB.the resistivities of their materials are (ρA)and(ρB).
View SolutionA cell develops the same power across two resistances R1 and R2 separately. The internal resistance of the cell is
View SolutionA cell develops the same power across two resistances R1 and R2 separately. The internal resistance of the cell is
View SolutionTwo particles of masses ma and mb and same charge are projected in a perpendicular magnetic field . They travel along circular paths of radius ra and rb such that ra>rb . Then which is true ?
View SolutionTwo particle are projected from an incliend plane as shown. A is projected up the incline and B down the incline. If RA and RB are range of A and B respectively then RBRA will be equal to :
 View Solution
View Solution

