Two resistors A and B have resistances RAandRBrespectively with RA<RB.the resistivities of their materials are (ρA)and(ρB).
(a)(ρA)>(ρB)
(b)(ρA)=(ρB)
(c ) (ρA)<(ρB)
(d) the information is not sufficient to find the relation between (ρA)and(ρB)
The correct Answer is:D
To solve the problem regarding the resistors A and B, we will analyze the given information step by step.
1. Understanding Resistance:
The resistance R of a conductor can be expressed using the formula:
R=ρ⋅LA
where ρ is the resistivity of the material, L is the length of the conductor, and A is the cross-sectional area.
2. Given Information:
We know that:
- Resistance of A: RA
- Resistance of B: RB
- It is given that RA<RB.
3. Relating Resistances to Resistivities:
Since we have two resistors, we can write their resistances as:
RA=ρA⋅LAAA
RB=ρB⋅LBAB
Here, ρA and ρB are the resistivities of materials A and B respectively, while LA,LB are their lengths and AA,AB are their cross-sectional areas.
4. Analyzing the Comparison:
Since RA<RB, we can write:
ρA⋅LAAA<ρB⋅LBAB
However, without additional information about the lengths and cross-sectional areas of the resistors, we cannot directly compare the resistivities ρA and ρB.
5. Conclusion:
The problem does not provide sufficient information to determine the relationship between the resistivities ρA and ρB. Therefore, we cannot conclude whether ρA>ρB, ρA<ρB, or ρA=ρB.
Final Answer:
The answer is that there is insufficient information to determine the relationship between the resistivities ρA and ρB.
---
The resistance R of a conductor can be expressed using the formula:
R=ρ⋅LA
where ρ is the resistivity of the material, L is the length of the conductor, and A is the cross-sectional area.
We know that:
- Resistance of A: RA
- Resistance of B: RB
- It is given that RA<RB.
Since we have two resistors, we can write their resistances as:
RA=ρA⋅LAAA
RB=ρB⋅LBAB
Here, ρA and ρB are the resistivities of materials A and B respectively, while LA,LB are their lengths and AA,AB are their cross-sectional areas.
Since RA<RB, we can write:
ρA⋅LAAA<ρB⋅LBAB
However, without additional information about the lengths and cross-sectional areas of the resistors, we cannot directly compare the resistivities ρA and ρB.
The problem does not provide sufficient information to determine the relationship between the resistivities ρA and ρB. Therefore, we cannot conclude whether ρA>ρB, ρA<ρB, or ρA=ρB.
The answer is that there is insufficient information to determine the relationship between the resistivities ρA and ρB.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - objective 2
9 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - Exercises
84 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - worked out Example
33 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
Similar Questions
Two metallic rings A and B identical in shape and size but having different resistivities ρA and ρB are kept on top of two idential solenoids as shown in the figure.When current I is switched on in both the solenoids in identical manner, the rings A and B jump to heights hA and hB respectively with hA > hB. The possible relation(s) between their resistivities and their masses mA and mB is (are)
View SolutionTwo strings A and B of lengths,LA=80cm and LB=xcm respectively are used separately in a sonometer. The ratio of their densities (ρA/ρB) is 0.81. The diameter of B is one-half that of A.if the strings have the same tension and fundamental frequency the value of x is
View Solution
Knowledge Check
Two soap bubbles A and B have radii r1andr2 respectively. If r1<r2 than the excess pressure inside
Abubbles A and B will be equalBbubbles A will be less than that in bubbles BCbubbles A will be greater than that in bubble BDbubbles A and B will be zero.
The circular orbit of two satellites have radii r1 and r2 respectively (r1<r2). If angular velosities of satellites are same, then their centripetal accelerations are related as
View SolutionTwo resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
View SolutionTwo resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
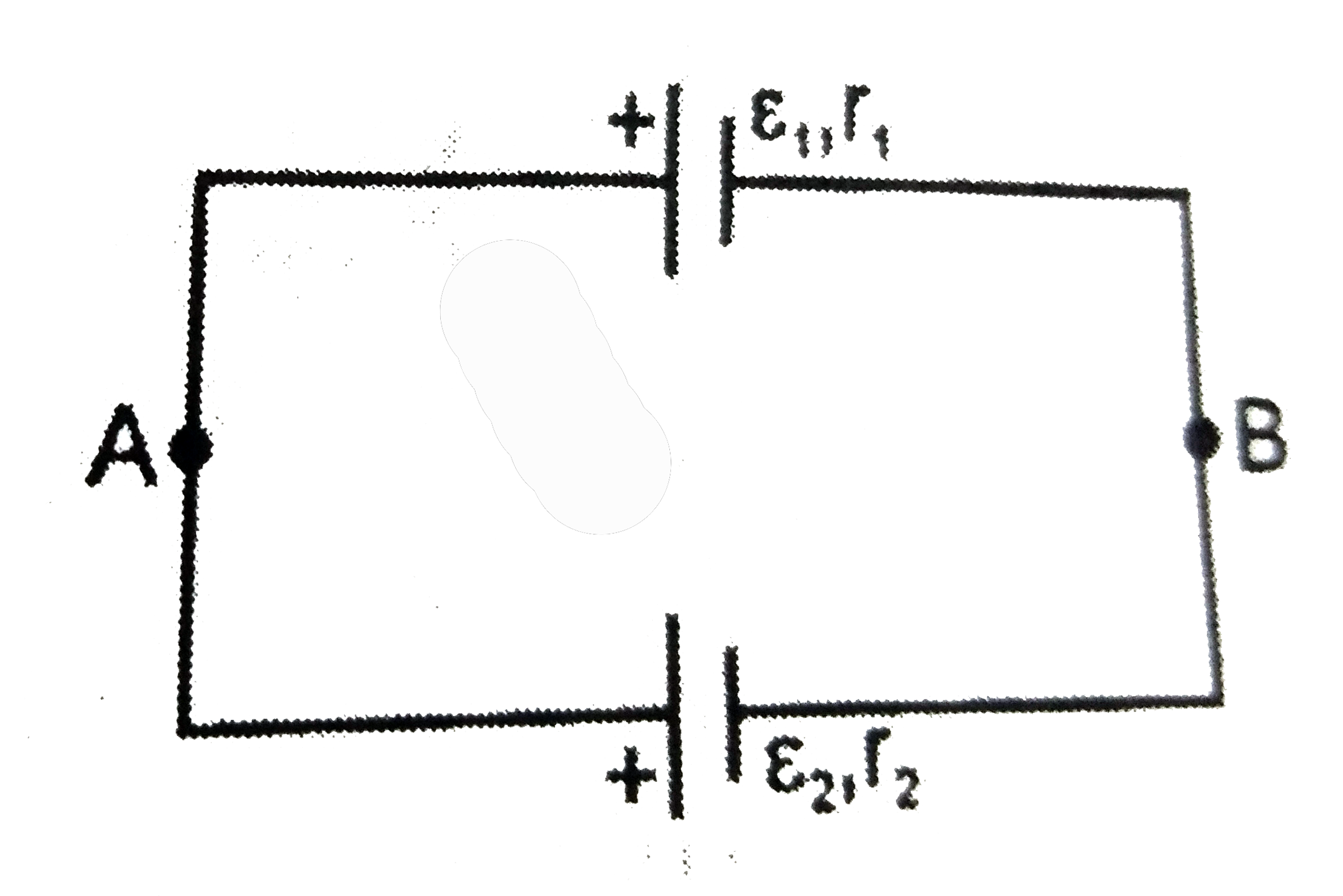
View SolutionTwo cells of unequal emfs ε1 and ε2, and internal resistances r1 and r2 are joined as shown. VA and VB are the potentials as A and B respectively.
View SolutionIn the, Ohm's law experiment ot find resistance of unknown resistor R, the arrangement is as shown. The resistance measured is given by Rmeasured=ViV= voltage reading of voltmeter. i=current reading of ammeter. The ammeters and the voltmeter used are not ideal, and have resistance RA and RV respectively. For arrangement shown, the meausred resistance is

View SolutionThe temperature coefficient of resistance for two material A and B are 0.0031∘C−1 and 0.0068∘C−1 respectively .Two resistance R1andR2 made from material A and B respectively . Have resistance of 200Ω and 100Ω at 0∘C. Show as a diagram the colour cube of a carbon resistance that would have a resistance equal to the series combination of R1andR2 at a temperature of 100∘C (Neglect the ring corresponding to the tolerance of the carbon resistor)
View SolutionTwo identical capacitors A and B are charged to the same potential and then made to discharge through resistances RA and RB respectively, with RA>RB.
View Solution
