Two identical charges are placed at the two corners of an equilateral triangle. The potential energy of the system is U. The work done in bringing an identical charge from infinity to the third vertex is
U
2U
3U
4U
The correct Answer is:B
To solve the problem of finding the work done in bringing an identical charge from infinity to the third vertex of an equilateral triangle where two identical charges are already placed at the other two vertices, we can follow these steps:
1. Understanding the Initial Configuration:
- We have two identical charges q placed at two corners of an equilateral triangle with side length a.
- The potential energy of this system is given as U.
2. Calculating the Initial Potential Energy:
- The potential energy U of the two charges can be calculated using the formula:
U=kq2a
- Here, k is Coulomb's constant.
3. Introducing the Third Charge:
- Now, we bring an identical charge q from infinity to the third vertex of the triangle.
- This charge will interact with the two existing charges.
4. Calculating the Final Potential Energy:
- When the third charge is brought to the third vertex, the potential energy of the new system (with three charges) can be calculated.
- The potential energy U′ of the system with three charges is the sum of the potential energies of each pair:
U′=U12+U23+U31
- Each pair contributes kq2a to the potential energy:
U′=kq2a+kq2a+kq2a=3kq2a
- Since U=kq2a, we can express U′ as:
U′=3U
5. Calculating the Work Done:
- The work done W by the external agent in bringing the charge from infinity to the third vertex is equal to the change in potential energy:
W=U′−U
- Substituting the values we found:
W=3U−U=2U
Final Answer
The work done in bringing the identical charge from infinity to the third vertex is 2U.
---
- We have two identical charges q placed at two corners of an equilateral triangle with side length a.
- The potential energy of this system is given as U.
- The potential energy U of the two charges can be calculated using the formula:
U=kq2a
- Here, k is Coulomb's constant.
- Now, we bring an identical charge q from infinity to the third vertex of the triangle.
- This charge will interact with the two existing charges.
- When the third charge is brought to the third vertex, the potential energy of the new system (with three charges) can be calculated.
- The potential energy U′ of the system with three charges is the sum of the potential energies of each pair:
U′=U12+U23+U31
- Each pair contributes kq2a to the potential energy:
U′=kq2a+kq2a+kq2a=3kq2a
- Since U=kq2a, we can express U′ as:
U′=3U
- The work done W by the external agent in bringing the charge from infinity to the third vertex is equal to the change in potential energy:
W=U′−U
- Substituting the values we found:
W=3U−U=2U
The work done in bringing the identical charge from infinity to the third vertex is 2U.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
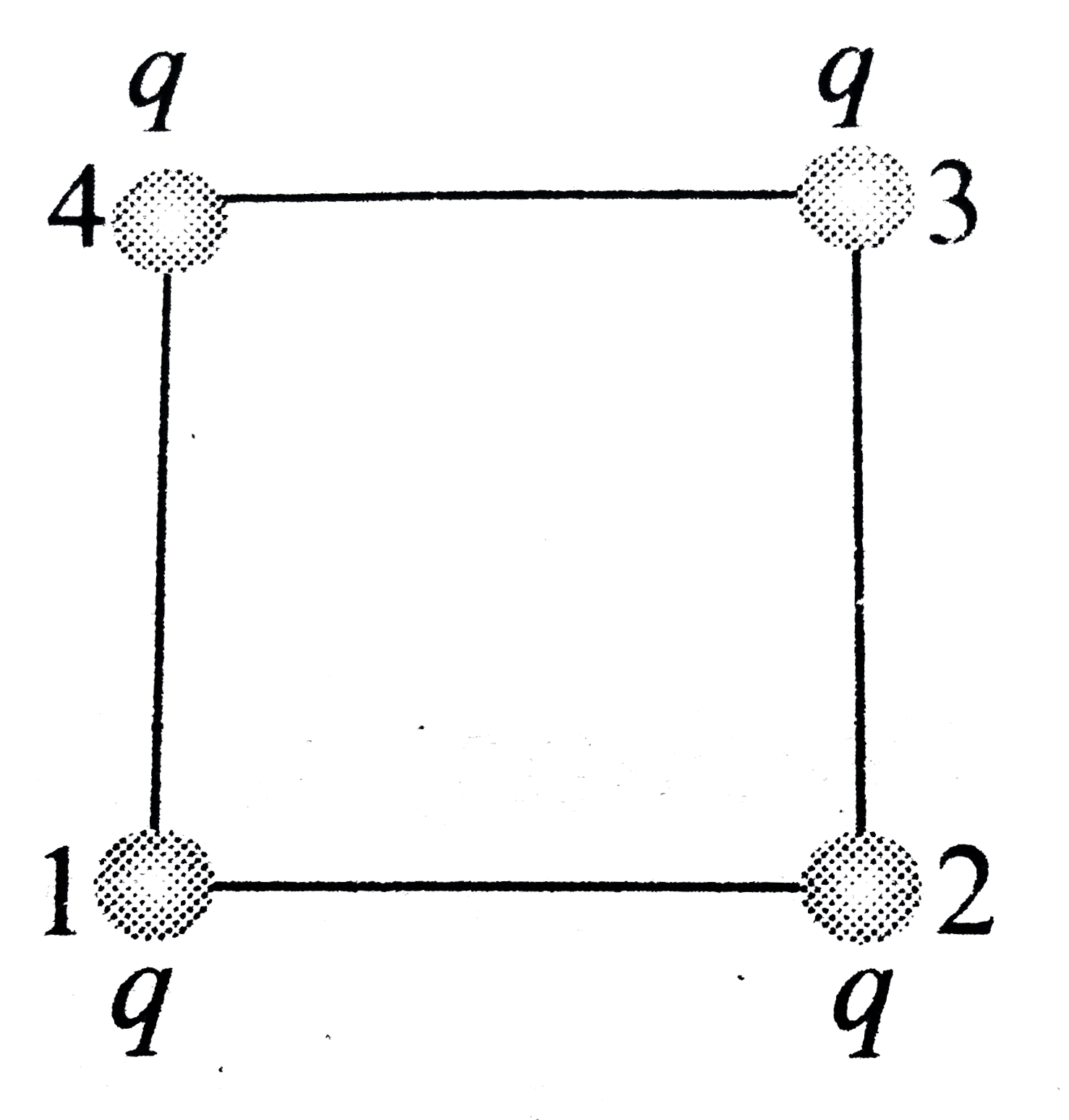
Four identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
 .
.
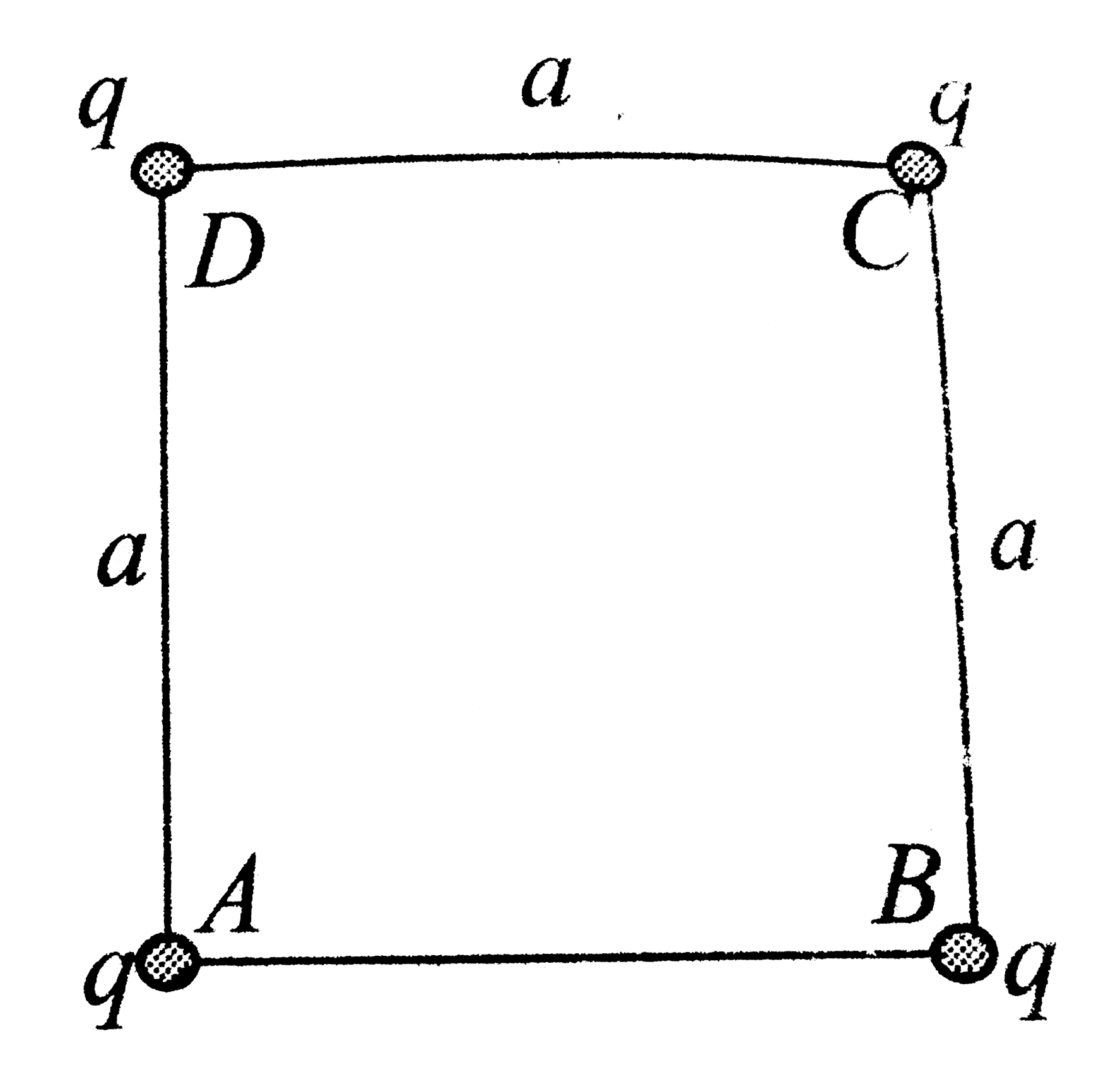
View SolutionFour identical charges q are placed at the corners of a square of side a. Find the potential energy of one of the charges due to the remaining charges.
 .
.
View Solution
Knowledge Check
In the question number 4, work done in bringing a charge of 4×10−9 C form infinity to that point is
A2.4×10−4JB1.8×10−4JC3.2×10−5JD4.1×10−5JElectric charges q,q,–2q are placed at the corners of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is
AqlB√3qlCzeroD4ql
Two equal charges q are placed at a distance of 2a and a third charge −2q is placed at the midpoint. The potential energy of the system is
View SolutionThree identical charges are placed at the vertices of an equilateral triangle. The force experienced by each charge, (if k=14πε0) is
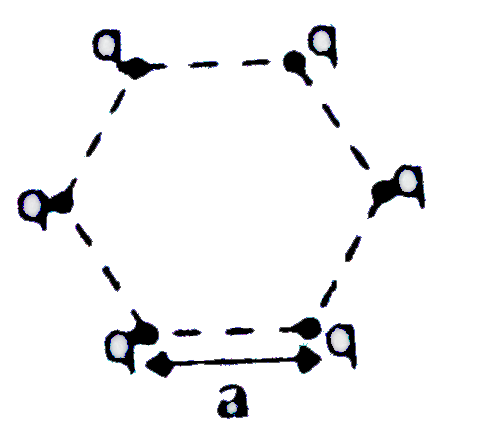
View SolutionSix equal point charges q each are placed at six corners of a hexago of side a. Find out potential energy of charge system
View SolutionIf 3 charges are placed at the vertices of equilateral triangle of charge 'q' each. What is the net potential energy, if the side of equilateral Δ is lcm ?
View SolutionElectric charges q,q,–2q are placed at the corners of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is
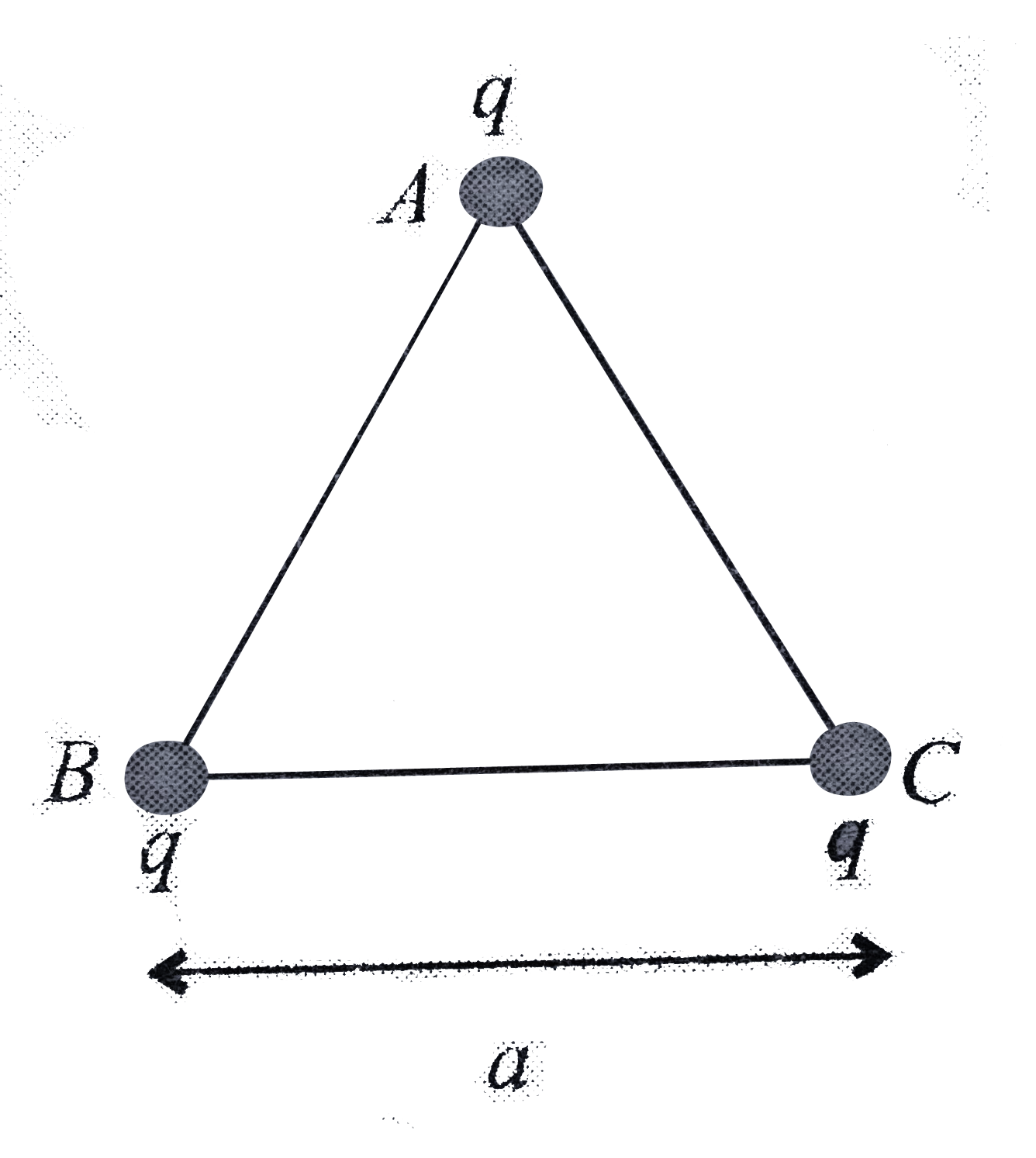
View SolutionThree equal charges q are placed at the corners of an equilateral triangle of side A.
(i) Find out potential energy of charge system.
(ii) Calculate work required to decrease the side of triangle to a/2.
(iii) If the charges are released from the shown position and each of them has same mass m, then find the speed of each particle when they lie on triangle of side 2a.
 .
.
View Solution
