Three identical charges are placed at the vertices of an equilateral triangle. The force experienced by each charge, (if k=14πε0) is
2Kq2r2
Kq22r2
√3Kq2r2
Kq2√2r2
The correct Answer is:C
To solve the problem of calculating the force experienced by each charge placed at the vertices of an equilateral triangle, we can follow these steps:
Step 1: Understand the Configuration
We have three identical charges, say Q, placed at the vertices of an equilateral triangle. Let the distance between each pair of charges be R.
Step 2: Calculate the Force Between Two Charges
Using Coulomb's Law, the force F between any two charges Q separated by a distance R is given by:
F=kQ2R2
where k=14πϵ0.
Step 3: Identify Forces Acting on One Charge
Consider one charge (let's say charge at vertex A). It experiences forces due to the other two charges (at vertices B and C). Let the force exerted by charge B on charge A be F1 and the force exerted by charge C on charge A be F2.
Since the charges are identical and symmetrically placed, we have:
F1=F2=F=kQ2R2
Step 4: Determine the Angle Between Forces
The angle between the forces F1 and F2 is 60∘ because the triangle is equilateral.
Step 5: Calculate the Resultant Force
To find the net force F acting on charge A due to charges B and C, we can use the law of cosines or the parallelogram law. The resultant force can be calculated as:
F=√F21+F22+2F1F2cos(60∘)
Substituting F1=F2=F:
F=√F2+F2+2F2⋅12=√2F2+F2=√3F2=√3F
Step 6: Substitute for F
Now substituting F=kQ2R2:
F=√3⋅kQ2R2
Final Answer
Thus, the force experienced by each charge is:
F=√3⋅kQ2R2
We have three identical charges, say Q, placed at the vertices of an equilateral triangle. Let the distance between each pair of charges be R.
Using Coulomb's Law, the force F between any two charges Q separated by a distance R is given by:
F=kQ2R2
where k=14πϵ0.
Consider one charge (let's say charge at vertex A). It experiences forces due to the other two charges (at vertices B and C). Let the force exerted by charge B on charge A be F1 and the force exerted by charge C on charge A be F2.
F1=F2=F=kQ2R2
The angle between the forces F1 and F2 is 60∘ because the triangle is equilateral.
To find the net force F acting on charge A due to charges B and C, we can use the law of cosines or the parallelogram law. The resultant force can be calculated as:
F=√F21+F22+2F1F2cos(60∘)
Substituting F1=F2=F:
F=√F2+F2+2F2⋅12=√2F2+F2=√3F2=√3F
Now substituting F=kQ2R2:
F=√3⋅kQ2R2
Thus, the force experienced by each charge is:
F=√3⋅kQ2R2
Similar Questions
Three charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
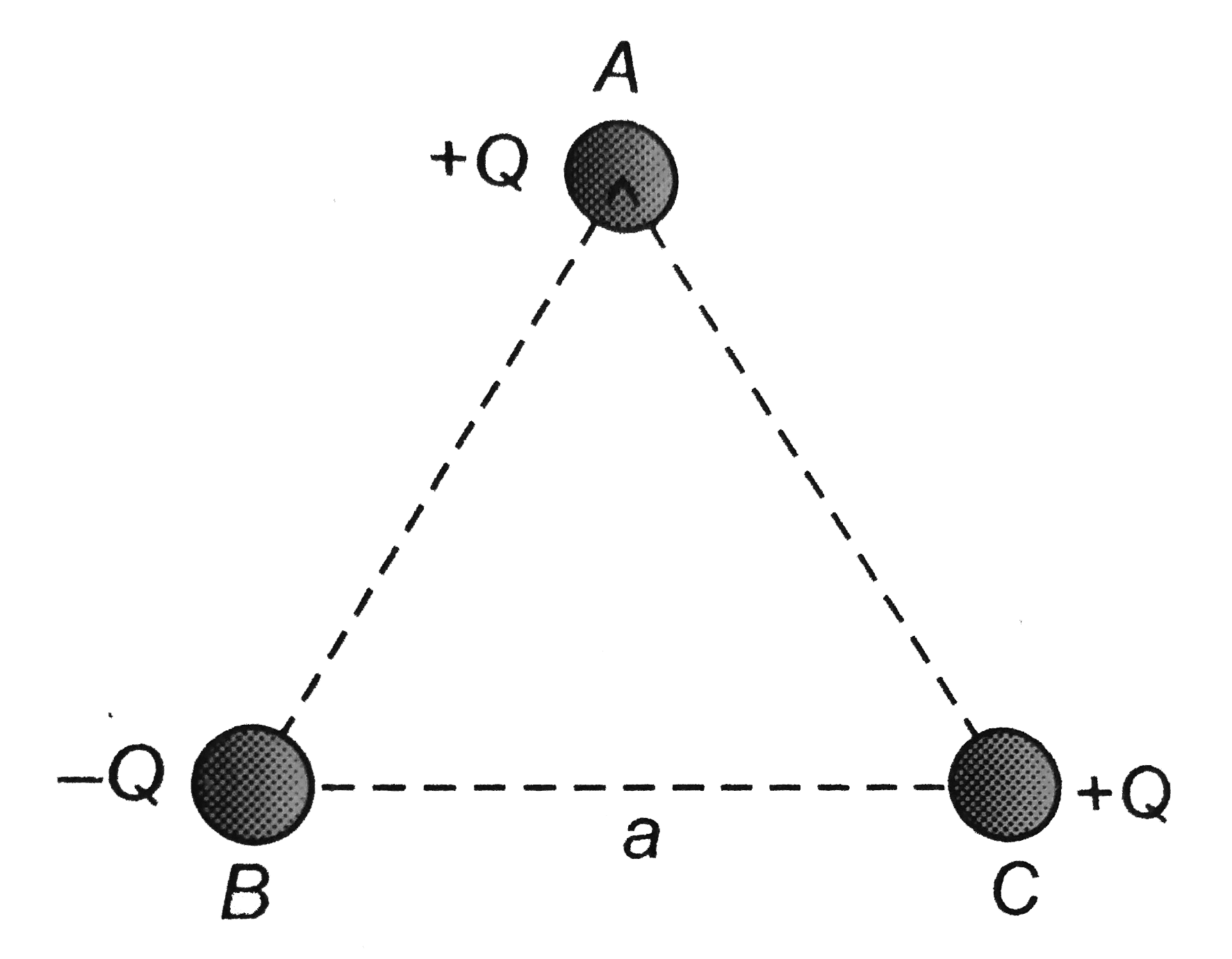
View SolutionThree charges are placed at the vertices of an equilateral trianlge of side a as shown in the following figure. The force experienced by the charge placed at the vertex A in a direction normal to BC is
View Solution
Knowledge Check
Consider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
Aq24√2πε0l2B−q24πε0l2Cq24πε0l2Dzero
Three charges are placed at the vertices of an equilateral trianlge of side a as shown in the following figure. The force experienced by the charge placed at the vertex A in a direction normal to BC is

View SolutionThree identical positive charges Q are arranged at the vertices of an equilateral triangle. The side of the triangle is a. Find the intensity of the field at the vertex of a regular tetrahedron of which the triangle is the base.
View SolutionThree identical particles each of mass m are placed at the vertices of an equilateral triangle of side a. Fing the force exerted by this system on a particle P of mass m placed at the

(a) the mid point of a side
(b) centre of the triangle
View SolutionThree identical charges are placed at corners of a equilateral triangel of side l. If force between any two charges is F, the work required to double the dimensiions of triangle is
View SolutionThree identical charges are placed at corners of a equilateral triangel of side l. If force between any two charges is F, the work required to double the dimensiions of triangle is
View SolutionThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
View SolutionThree equal charges Q are placed at the three vertices of an equilateral triangle. What should be the va,ue of a charge, that when placed at the centroid, reduces the interaction energy of the system to zero ?
View Solution
