Two identical cylindrical vessels are kept on the ground and each contain the same liquid of density d. The area of the base of both vessel is x1 and in the other, x2. When both cylinders are connected through a pipe of negligible volume very close to the bottom, the liquid flows from one vessel to the other until it comes to equilibrium at a new height. The change in energy of the system in the process is :
gdS(x22+x21)
14gdS(x2−x1)2
34gdS(x2−x1)2
gdS(x2+x1)2
To solve the problem of finding the change in energy of the system when two identical cylindrical vessels containing the same liquid are connected, we can follow these steps:
Step 1: Understand the Initial Setup
We have two identical cylindrical vessels with liquid of density d. The heights of the liquid in the vessels are x1 and x2 respectively. The area of the base of the first vessel is S1 and for the second vessel is S2.
Step 2: Calculate Initial Potential Energy
The potential energy of a liquid column in a cylinder is given by the formula:
PE=12×density×volume×g×height of center of mass
For the first vessel:
- Volume V1=S1⋅x1
- Center of mass height = x12
Thus, the potential energy PE1 of the first vessel is:
PE1=12⋅d⋅(S1⋅x1)⋅g⋅x12=d⋅S1⋅g⋅x214
For the second vessel:
- Volume V2=S2⋅x2
- Center of mass height = x22
Thus, the potential energy PE2 of the second vessel is:
PE2=12⋅d⋅(S2⋅x2)⋅g⋅x22=d⋅S2⋅g⋅x224
The total initial potential energy PEinitial is:
PEinitial=PE1+PE2=d⋅S1⋅g⋅x214+d⋅S2⋅g⋅x224
Step 3: Determine Final Height
When the liquid reaches equilibrium, the heights in both vessels will be equal. Let this common height be x. Therefore, we have:
x=x1+x22
Step 4: Calculate Final Potential Energy
The potential energy for both vessels at the final height x is:
PEfinal=12⋅d⋅(S1⋅x)⋅g⋅x2+12⋅d⋅(S2⋅x)⋅g⋅x2
PEfinal=d⋅g⋅x4(S1+S2)x=d⋅g⋅(S1+S2)x24
Step 5: Calculate Change in Energy
The change in energy ΔU of the system is given by:
ΔU=PEfinal−PEinitial
Substituting the expressions we derived:
ΔU=d⋅g⋅(S1+S2)x24−(d⋅S1⋅g⋅x214+d⋅S2⋅g⋅x224)
Step 6: Simplify the Expression
This can be simplified further to find the exact change in energy based on the values of x1, x2, S1, and S2.
We have two identical cylindrical vessels with liquid of density d. The heights of the liquid in the vessels are x1 and x2 respectively. The area of the base of the first vessel is S1 and for the second vessel is S2.
The potential energy of a liquid column in a cylinder is given by the formula:
PE=12×density×volume×g×height of center of mass
- Volume V1=S1⋅x1
- Center of mass height = x12
PE1=12⋅d⋅(S1⋅x1)⋅g⋅x12=d⋅S1⋅g⋅x214
- Volume V2=S2⋅x2
- Center of mass height = x22
PE2=12⋅d⋅(S2⋅x2)⋅g⋅x22=d⋅S2⋅g⋅x224
PEinitial=PE1+PE2=d⋅S1⋅g⋅x214+d⋅S2⋅g⋅x224
When the liquid reaches equilibrium, the heights in both vessels will be equal. Let this common height be x. Therefore, we have:
x=x1+x22
The potential energy for both vessels at the final height x is:
PEfinal=12⋅d⋅(S1⋅x)⋅g⋅x2+12⋅d⋅(S2⋅x)⋅g⋅x2
PEfinal=d⋅g⋅x4(S1+S2)x=d⋅g⋅(S1+S2)x24
The change in energy ΔU of the system is given by:
ΔU=PEfinal−PEinitial
Substituting the expressions we derived:
ΔU=d⋅g⋅(S1+S2)x24−(d⋅S1⋅g⋅x214+d⋅S2⋅g⋅x224)
This can be simplified further to find the exact change in energy based on the values of x1, x2, S1, and S2.
Topper's Solved these Questions
Similar Questions
Two identical cylindrical vessels have the same base area but are filled with different volumes of water . The forces on the bases of the two vessels are same .
View SolutionTwo identical cylindrical vessels with their bases at the same level each, contain a liquid of density ρ. The area of either base is A but in one vessel the liquid heigth is h1 and in the other liquid height is h2(h2<h1). If the two vessel are connected, the work done by gravity in equalizing the level is
View Solution
Knowledge Check
Two identical cylindrical vessels with their bases at the same level each, contain a liquid of density ρ. The area of either base is A but in one vessel the liquid height is h1 and in the other liquid height is h2(h2<h1). If the two vessel are connected, the work done by gravity in equalizing the level is
A12(h1−h2)2AρgB12(h1+h2)2AρgC12(h21−h22)2AρgD14(h1−h2)2AρgA cylindrical vessel, which has radius 6 cm and length 21 cm , contains liquid. The volume (in cu cm) of liquid in the vessel is :
A1584B1680C1507D1820To what height h should a cylindrical vessel of diameter d be filled with a liquid so that the total force on the vertical surface of the vessel be equal to the force on the bottom-
Ah=dBh=2dCh=3dDh=d/2
Two identical cylindrical vessels with their bases at the same level each contain a liquid of density 1.30×103kg/m3. The area of each base is 4.25cm2 , but in one vessel the liquid height is 0.854 m and in the other it is 1.560 m. Find the work done by the gravitational force in equalizing the levels when the two vessels are connected
View SolutionA lipuid is poured into a cylindrical vessel of height H and mass M. to what height a liquid of density p should be poured so that the centre of gravity of the vessel + kuqyud ' sustem mat be at the minimum height from the bottom . Negalect the mass of the bottom .the area of cross - section of the vessel of A .
View SolutionThe vapour pressure of a liquid in a closed container depends upon
View SolutionA liquid of density ρ is filled in two indentical cylindrical vessels with base area A and height of the liquid in one vessel is h1 and that in the other vessel is h2. If both the vesels are connected with their base at the same level then calculate the work done by gravity in equalizing the levels.
View SolutionA uniformly tapering vessel is filled with a liquid of density 900km/m3. The force that acts on the base of the vessel due to the liquid is (g=10ms−2)
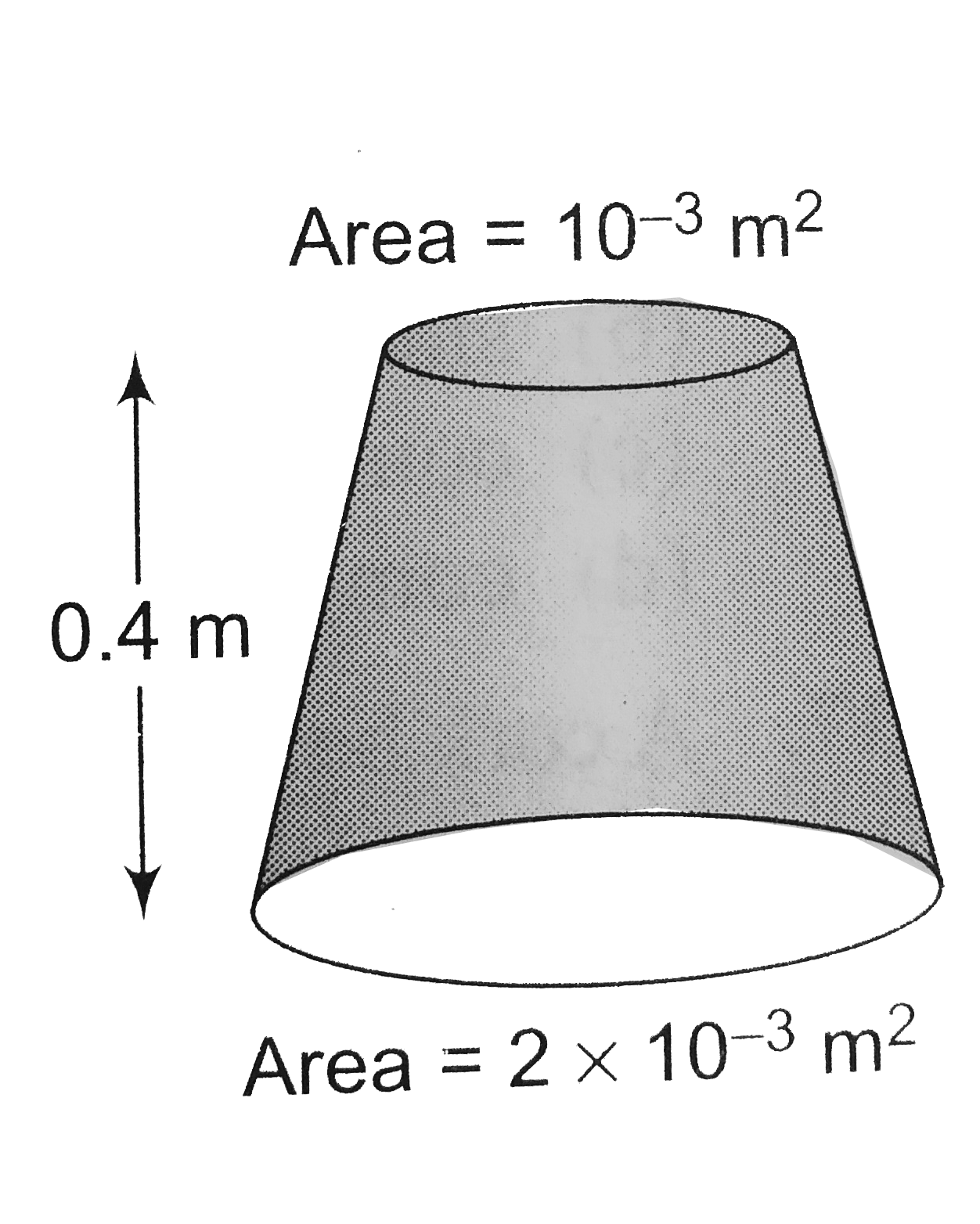
View Solution
