A liquid of density ρ is filled in two indentical cylindrical vessels with base area A and height of the liquid in one vessel is h1 and that in the other vessel is h2. If both the vesels are connected with their base at the same level then calculate the work done by gravity in equalizing the levels.
(h1−h2)gρ
(h1−h2)gAρ
12(h1−h2)2gAρ
14(h1−h2)2gAρ
The correct Answer is:D
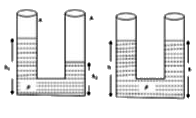
Here h is the average of h1 and h2
So h=h1+h22
And
Δh=h1−h
=h1−(h1+h22)
=(h1−h22)
Mass of liquid dispalced is
ρ=mV
m=ρV
m=ρ×A×Δh
m=ρ×A×(h1−h22)
Where ρ= density of liquid
A= area of vessel
V=volume of liquid displaced
W=−ΔU
W=mgΔh
W=ρgA=(h1−h22)×(h1−h22)
W=ρgA4(h1−h2)2
Topper's Solved these Questions
Similar Questions
Two identical cylindrical vessel with their bases at the same level each contain a liquid of density ρ. The height of the liquid in one vessel is h1 and in the other is h2 the area of either base is A. What is the work done by gravity is equalising the levels when the two vessels are connected?
View SolutionTwo identical cylindrical vessels with their bases at the same level each, contain a liquid of density ρ. The area of either base is A but in one vessel the liquid heigth is h1 and in the other liquid height is h2(h2<h1). If the two vessel are connected, the work done by gravity in equalizing the level is
View Solution
Knowledge Check
Two identical cylindrical vessels with their bases at the same level each, contain a liquid of density ρ. The area of either base is A but in one vessel the liquid height is h1 and in the other liquid height is h2(h2<h1). If the two vessel are connected, the work done by gravity in equalizing the level is
A12(h1−h2)2AρgB12(h1+h2)2AρgC12(h21−h22)2AρgD14(h1−h2)2AρgTwo cylindrical vessels of equal cross-sectional area. A contain water upto height h1 and h2. The vessels are interconnected so that the levels in them becomes equal. The work done by the force of gravity during the process is:
AzeroBρA(h1+h22)2gCρA(h1−h22)2gDρAh1h22g
Two identical cylindrical vessels with their bases at the same level each, contain a liquid of density ρ. The area of either base is A but in one vessel the liquid heigth is h1 and in the other liquid height is h2(h2<h1). If the two vessel are connected, the work done by gravity in equalizing the level is
View SolutionTwo identical cylindrical vessels have the same base area but are filled with different volumes of water . The forces on the bases of the two vessels are same ?
View SolutionTwo identical cylindrical vessels have the same base area but are filled with different volumes of water . The forces on the bases of the two vessels are same .
View SolutionTwo identical cylindrical vessel with their bases at the same level each contain a liquid of density ρ. The height of the liquid in one vessel is h1 and in the other is h2 the area of either base is A. What is the work done by gravity is equalising the levels when the two vessels are connected?
View SolutionTwo immiscible liquids of densities d and 2d are taken in a cylindrical vessel with equal heights each h. The velocity efflux of the liquid coming out of the hole made to the wall of the vessel at its bottom is
View SolutionTwo cyllindrical vessels of equal cross sectional ara A contain water upto heights h1 and h2. The vessels are interconnected so that the levels in them become equal. Calculate the work done by the force of gravity during the process. The density of water is ρ
View Solution
