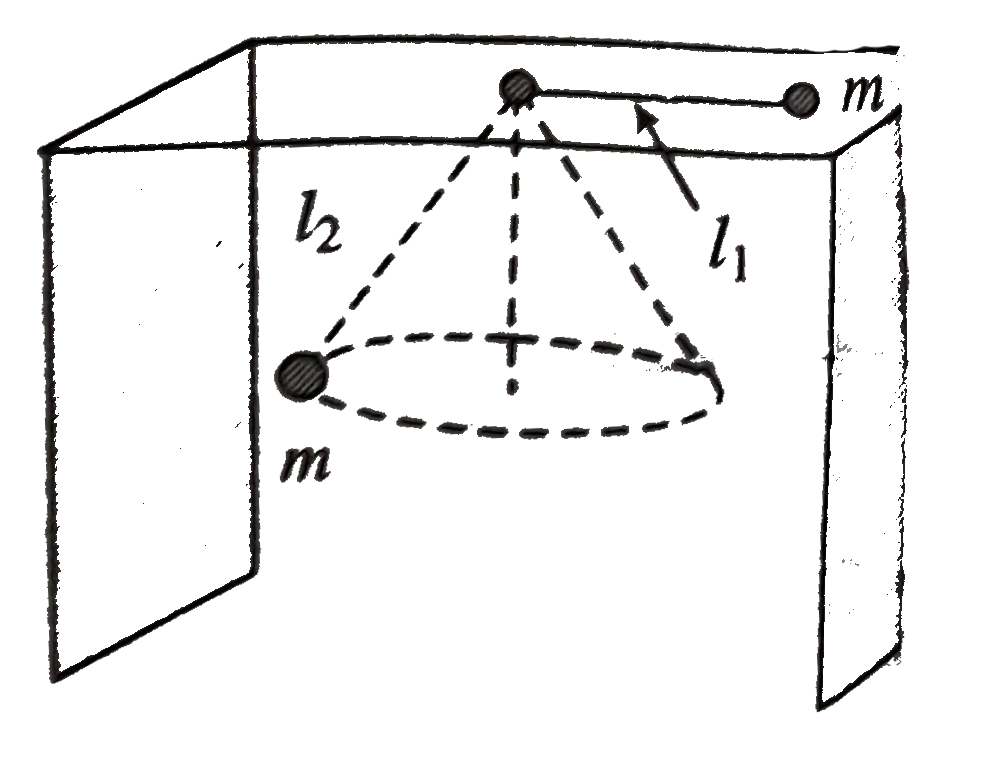
Two identical particles are attached at the end of a light string which passes through a hole at the center of a table One of the partical is made to move in a circle on a table with angular velocity $ω_{1}$ and the ther is made a move is a horizontal $ω_{2}$ if $l_{1}$ and $l_{2}$ are the length the table , than in order that particle under down the table neither moves down nor move up the ratio $l_{1} / l_{2}$ is

$\frac{ω_{1}}{ω_{2}}$

$\frac{ω_{2}}{ω_{1}}$

$\frac{ω_{1}^{2}}{ω_{2}^{2}}$

$\frac{ω_{2}^{2}}{ω_{1}^{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$T = m ω_{1}^{2} l_{1}$ …(i)
$T sin θ = m ω_{2}^{2} l_{2} sin θ \Rightarrow T = m ω_{2}^{2} l_{2}$ …(ii)
$\Rightarrow \frac{l_{1}}{l_{2}} = \frac{ω_{2}^{2}}{ω_{1}^{2}}$

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Knowledge Check

Two identical particle are attached at the ends of a light string which passes through a hole at the centre of a table another particle on the table is made to revolve with angular velocity $ω_{1}$ . One of the particles is made to move in a horizontal circle as a conical pendulum with angular velocity $ω_{2}$ . If $l_{1}$ and $l_{2}$ are the length of the string over and under the table , then in order that particle under the table neither moves down nor moves up the ratio $\frac{l_{1}}{l_{2}}$ is :

A $\frac{ω_{1}}{ω_{2}}$
B $\frac{ω_{2}}{ω_{1}}$
C $\frac{ω_{1}^{2}}{ω_{2}^{2}}$
D $\frac{ω_{2}^{2}}{ω_{1}^{2}}$
Two particles, each of mass m are attached to the two ends of a light string of length l which passes through a hole at the centre of a table. One particle describes a circle on the table with angular velocity $ω_{1}$ and the other describes a circle as a conical pendulum with angular velocity $ω_{2}$ below the table as shown in figure -3.86. if $l_{1}$ and $l_{2}$ are the lengths of the portion of the string above and below the table then :

A $\frac{l_{1}}{l_{2}} = \frac{ω_{2}^{2}}{ω_{1}^{2}}$
B $\frac{l_{1}}{l_{2}} = \frac{ω_{1}^{2}}{ω_{2}^{2}}$
C $\frac{1}{ω_{1}^{2}} + \frac{1}{ω_{2}^{2} = \frac{l}{g}}$
D $\frac{1}{ω_{1}^{2}} + \frac{1}{ω_{2}^{2}} > \frac{l}{g}$
A particle of mass m is attached to one end of a string of length l while the other end is fixed to a point h above the horizontal table. The particle is made to revolve in a circle on the table so as to make p revolutions per second. The maximum value of p if the particle is to be in contact with the table will be :
A $2 π \sqrt{g h}$
B $\sqrt{g / h}$
C $2 π \sqrt{h / g}$
D $\frac{1}{2 π} \sqrt{g / h}$

CENGAGE PHYSICS-NEWTON'S LAWS OF MOTION 2-Single Correct

Home
Ask Doubt
Profile

The correct Answer is:D

T=mω21l1 …(i) Tsinθ=mω22l2sinθ⇒T=mω22l2…(ii) ⇒l1l2=ω22ω21

Topper's Solved these Questions

Similar Questions

Knowledge Check

CENGAGE PHYSICS-NEWTON'S LAWS OF MOTION 2-Single Correct

$T = m ω_{1}^{2} l_{1}$ …(i)
$T sin θ = m ω_{2}^{2} l_{2} sin θ \Rightarrow T = m ω_{2}^{2} l_{2}$ …(ii)
$\Rightarrow \frac{l_{1}}{l_{2}} = \frac{ω_{2}^{2}}{ω_{1}^{2}}$