Two identical rings PandQ of radius 0.1m are mounted coaxially at a distance 0.5m apart. The charges on the two rings are 2μCand4μC, respectively. The work done in transferring a charge of 5μC from the center of P to that of Q is.
1.28 J
0.72 J
0.144 J
2.24 J
The correct Answer is:b
To solve the problem step by step, we will calculate the electric potential at the centers of the rings P and Q and then find the work done in transferring a charge from the center of ring P to the center of ring Q.
Step 1: Calculate the potential at the center of ring P
The potential VP at the center of ring P due to its own charge can be calculated using the formula:
VP=k⋅QPRP
where:
- k=14πϵ0≈9×109N m2/C2
- QP=2μC=2×10−6C
- RP=0.1m
Substituting the values:
VP=9×109⋅2×10−60.1=180000V=1.8×105V
Step 2: Calculate the potential at the center of ring Q
The potential VQ at the center of ring Q due to its own charge is:
VQ=k⋅QQRQ
where:
- QQ=4μC=4×10−6C
- RQ=0.1m
Substituting the values:
VQ=9×109⋅4×10−60.1=360000V=3.6×105V
Step 3: Calculate the distance from the center of ring P to the center of ring Q
The distance d between the centers of the two rings is given as 0.5m. The distance from the center of ring P to the center of ring Q can be calculated using the Pythagorean theorem:
d=√(0.5)2+(0.1)2=√0.25+0.01=√0.26≈0.51m
Step 4: Calculate the potential at the center of ring P due to ring Q
The potential at the center of ring P due to the charge on ring Q is:
VPQ=k⋅QQd
Substituting the values:
VPQ=9×109⋅4×10−60.51≈705882.35V
Step 5: Calculate the potential at the center of ring Q due to ring P
The potential at the center of ring Q due to the charge on ring P is:
VQP=k⋅QPd
Substituting the values:
VQP=9×109⋅2×10−60.51≈352941.18V
Step 6: Calculate the total potential at the centers
The total potential at the center of ring P:
VtotalP=VP+VPQ=1.8×105+705882.35≈8.5888235×105V
The total potential at the center of ring Q:
VtotalQ=VQ+VQP=3.6×105+352941.18≈7.941176×105V
Step 7: Calculate the work done in transferring the charge
The work done W in transferring a charge q from point P to point Q is given by:
W=q⋅(VtotalQ−VtotalP)
where:
- q=5μC=5×10−6C
Substituting the values:
W=5×10−6⋅(7.941176×105−8.5888235×105)
Calculating the difference:
W=5×10−6⋅(−647647.35)≈−3.238×10−6J
The negative sign indicates that work is done against the electric field.
Final Answer
The work done in transferring the charge from the center of ring P to that of ring Q is approximately −3.238×10−6J.
---
VP=k⋅QPRP
where:
- k=14πϵ0≈9×109N m2/C2
- QP=2μC=2×10−6C
- RP=0.1m
VP=9×109⋅2×10−60.1=180000V=1.8×105V
VQ=k⋅QQRQ
where:
- QQ=4μC=4×10−6C
- RQ=0.1m
VQ=9×109⋅4×10−60.1=360000V=3.6×105V
d=√(0.5)2+(0.1)2=√0.25+0.01=√0.26≈0.51m
VPQ=k⋅QQd
Substituting the values:
VPQ=9×109⋅4×10−60.51≈705882.35V
VQP=k⋅QPd
Substituting the values:
VQP=9×109⋅2×10−60.51≈352941.18V
VtotalP=VP+VPQ=1.8×105+705882.35≈8.5888235×105V
VtotalQ=VQ+VQP=3.6×105+352941.18≈7.941176×105V
W=q⋅(VtotalQ−VtotalP)
where:
- q=5μC=5×10−6C
W=5×10−6⋅(7.941176×105−8.5888235×105)
Calculating the difference:
W=5×10−6⋅(−647647.35)≈−3.238×10−6J
The work done in transferring the charge from the center of ring P to that of ring Q is approximately −3.238×10−6J.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Multiple Correct
10 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Comprehension
31 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Subjective
28 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
Two identical thin rings each of radius R are coaxially placed at a distance R. If the rings have a uniform mass distribution and each has masses 2m and 4m respectively, then the work done in moving a mass m from centre of one ring to that of the other is
View SolutionTwo identical thin ring each of radius R are co-axially placed at a distance R. If the ring have a uniform mass distribution and each has mass m1 and m2 respectively, then the work done in moving a mass m from the centre of one ring to that of the other is :
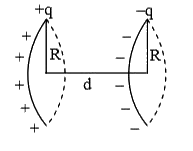
View SolutionTwo thin rings each of radius R are placed at a distance 'd' apart. The charges on the rings are +q and -q. The potential difference between their centres will be -
View SolutionTwo identical thin ring, each of radius R meters, are coaxially placed a distance R metres apart. If Q1 coulomb, and Q2 coulomb, are repectively the charges uniformly spread on the two rings, the work done in moving a charge q from the centre of one ring to that of the other is
View SolutionTwo identical thin ring, each of radius R meters, are coaxially placed a distance R metres apart. If Q1 coulomb, and Q2 coulomb, are repectively the charges uniformly spread on the two rings, the work done in moving a charge q from the centre of one ring to that of the other is
View SolutionTwo positive point charges of 12μC and 8μC are 10cm apart. The work done in bringing then 4cm closer is
View SolutionTwo positive point charges of 12μC and 8μC are 10cm apart. The work done in bringing then 4cm closer is
View SolutionTwo identicaln thin rings each of radius 10 cm carrying charges 10 C and 5 C are coaxially placed at a distance 10 cm apart. The work done in moving a charge q from the centre of the first ring to that of the second is
View SolutionA charge of 5μC is placed at the center of a square ABCD of side 10cm. Find the work done (inμJ) in moving a charge of 1μC from A to B.
View SolutionTwo identical coaxial rings each of radius R are separated by a distance of √3R. They are uniformly charged with charges +Q and −Q respectively. The minimum kinetic energy with which a charged particle (charge +q) should be projected from the centre of the negatively charged ring along the axis of the rings such that it reaches the centre of the positively charged ring is
View Solution
