Two identical samples (same material and same amout) P and Q of a radioactive substance having mean life T are observed to have activities and respectively at the time of observation. If P is older than Q, then the difference in their age is
(a)
(b)
(c)
(d)
The correct Answer is:B
To find the difference in age between two identical samples P and Q of a radioactive substance, we can follow these steps:
Step 1: Understand the relationship between activity and time
The activity A of a radioactive sample is given by the equation:
A=A0e−λt
where:
- A0 is the initial activity,
- λ is the decay constant,
- t is the time elapsed.
Step 2: Write the activity equations for both samples
For sample P (which is older), the activity at time t1 can be expressed as:
AP=A0e−λt1
For sample Q (which is younger), the activity at time t2 can be expressed as:
AQ=A0e−λt2
Step 3: Relate the mean life to the decay constant
The mean life T of a radioactive substance is related to the decay constant λ by:
T=1λ
Thus, we can express λ as:
λ=1T
Step 4: Express the ages in terms of activities
From the activity equations, we can take the natural logarithm to express the ages:
For sample P:
t1=−1λln(APA0)
For sample Q:
t2=−1λln(AQA0)
Step 5: Calculate the difference in age
Since sample P is older than sample Q, we find the difference in their ages:
Δt=t1−t2
Substituting the expressions for t1 and t2:
Δt=−1λln(APA0)+1λln(AQA0)
This simplifies to:
Δt=1λ(ln(AQA0)−ln(APA0))
Using the properties of logarithms, this can be rewritten as:
Δt=1λln(AQAP)
Step 6: Substitute λ with 1T
Substituting λ back in terms of mean life T:
Δt=Tln(AQAP)
Final Answer
Thus, the difference in their ages is:
Δt=Tln(AQAP)
The activity A of a radioactive sample is given by the equation:
A=A0e−λt
where:
- A0 is the initial activity,
- λ is the decay constant,
- t is the time elapsed.
For sample P (which is older), the activity at time t1 can be expressed as:
AP=A0e−λt1
For sample Q (which is younger), the activity at time t2 can be expressed as:
AQ=A0e−λt2
The mean life T of a radioactive substance is related to the decay constant λ by:
T=1λ
Thus, we can express λ as:
λ=1T
From the activity equations, we can take the natural logarithm to express the ages:
For sample P:
t1=−1λln(APA0)
For sample Q:
t2=−1λln(AQA0)
Since sample P is older than sample Q, we find the difference in their ages:
Δt=t1−t2
Substituting the expressions for t1 and t2:
Δt=−1λln(APA0)+1λln(AQA0)
This simplifies to:
Δt=1λ(ln(AQA0)−ln(APA0))
Using the properties of logarithms, this can be rewritten as:
Δt=1λln(AQAP)
Substituting λ back in terms of mean life T:
Δt=Tln(AQAP)
Thus, the difference in their ages is:
Δt=Tln(AQAP)
Topper's Solved these Questions
- MODERN PHYSICS - 2BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 2 More Than One Correct
6 Videos
- MODERN PHYSICS - 2BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 2 Comprehension Based
3 Videos
- MODERN PHYSICS - 2BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 1 Subjective Questions
1 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2 Subjective
23 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
Similar Questions
Two identical spheres of same mass and specific gravity (which is the ratio of density of a substance and density of water) 2.4 have different charges of Q and -3Q. They are suspended from two stings of a same length l fixed to points at the same horizontal level, but distant l from each other. When the entire set up is transferred inside a liquid of specific gravity 0.8, it is observed that the inclination of each string in equilibrium remains unchanged. Then the dielectric constant of the liquid is
View SolutionTwo radioactive samples of different elements (half-lives t1 and t2 respectively) have same number of nuclei at t=0. The time after which their activities are same is
View SolutionSuppose P and Q are two different matrices of order 3×n andn×p, then the order of the matrix P×Q is ?
View SolutionP and Q are two distinct points on the parabola, y2=4x with parameters t and t1 respectively. If the normal at P passes through Q, then the minimum value of t21 is
View SolutionTwo thick wires and tow thin wires, all of same material and same length from a squre in the three different ways P, Q and R as shown. The current flowing through the arrangement is i. Let BP,BQandBR represent the magnetic field at the centre of square in the three cases, then

View SolutionA capacitor of capacity C having charge q and 3q, on the plate P1 and P2 respectively as shoen in figure. Now switch 'S' is closed, find the work done by the battery. (take q=CV )

View SolutionTwo spring P and Q having stiffness constants k1 and k2(<k1), respectively are stretched equally. Then
View SolutionTwo identical discs of same radius R are rotating about their axes in opposite directions with the same constant angular speed ω . The discs are in the same horizontal plane. At time t=0 , the points P and Q are facing each other as shown in the figure. The relative speed between the two points P and Q is vr. In one time period (T) of rotation of the discs , vr as a function of time is best represented by
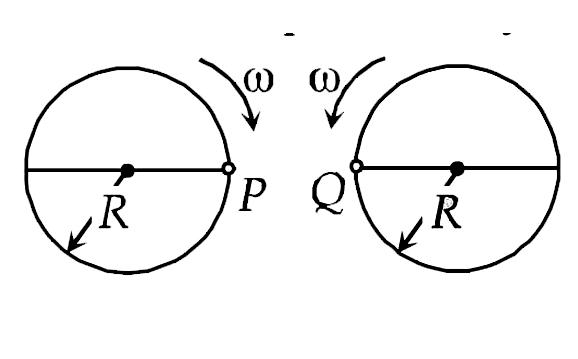
View SolutionTwo circles touch externally at a point P. From a external point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and R respectively. Prove that TQ=TR.
View SolutionFor a radioactive material, its activity A and rate of change of its activity of R are defined as A=−dNdt and R=−dAdt, where N(t) is the number of nuclei at time t. Two radioactive source P (mean life τ) and Q (mean life 2τ) have the same activity at t=0. Their rates of activities at t=2τ are Rp and RQ, respectively. If RPRQ=ne, then the value of n is:
View Solution
