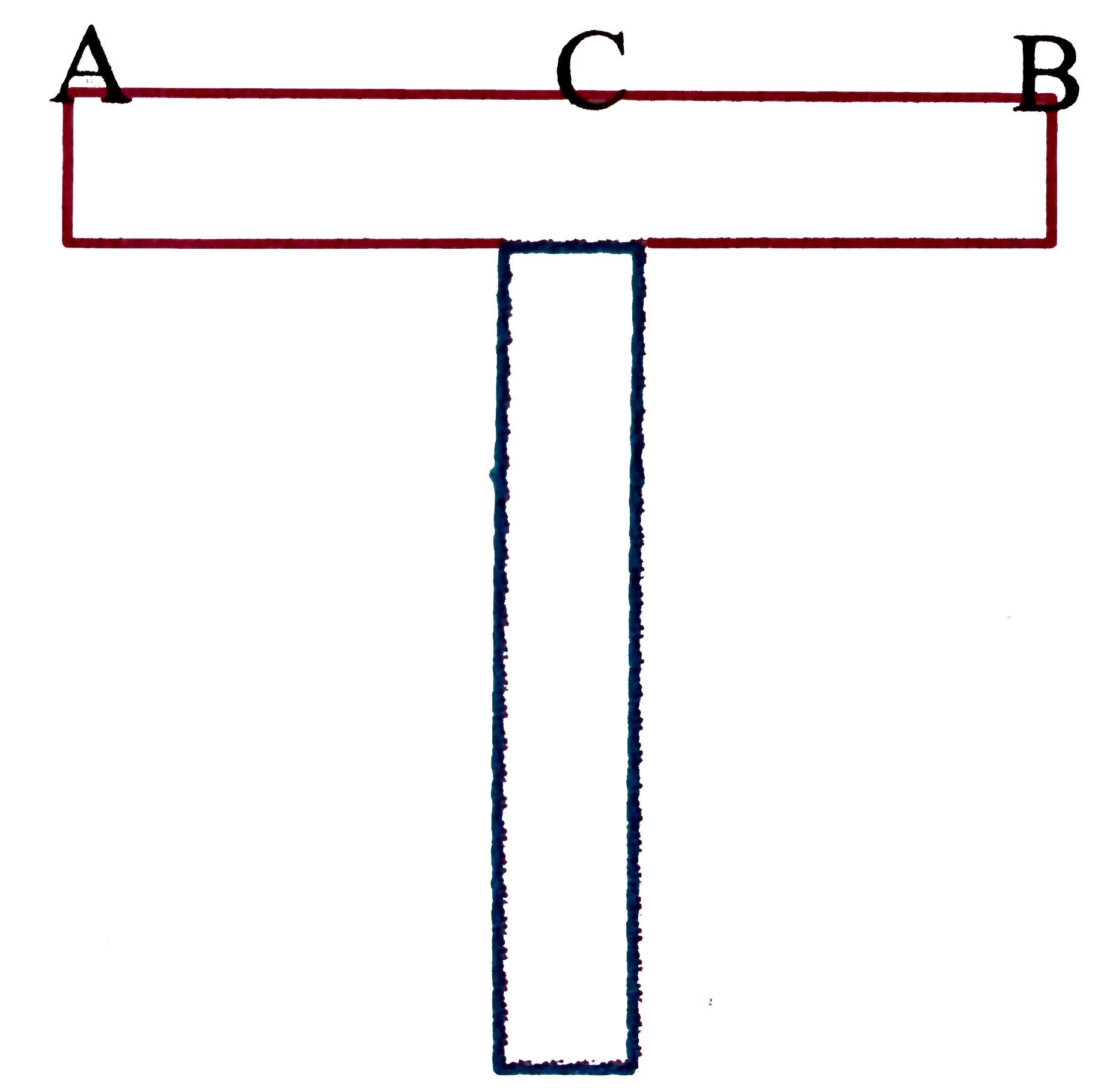
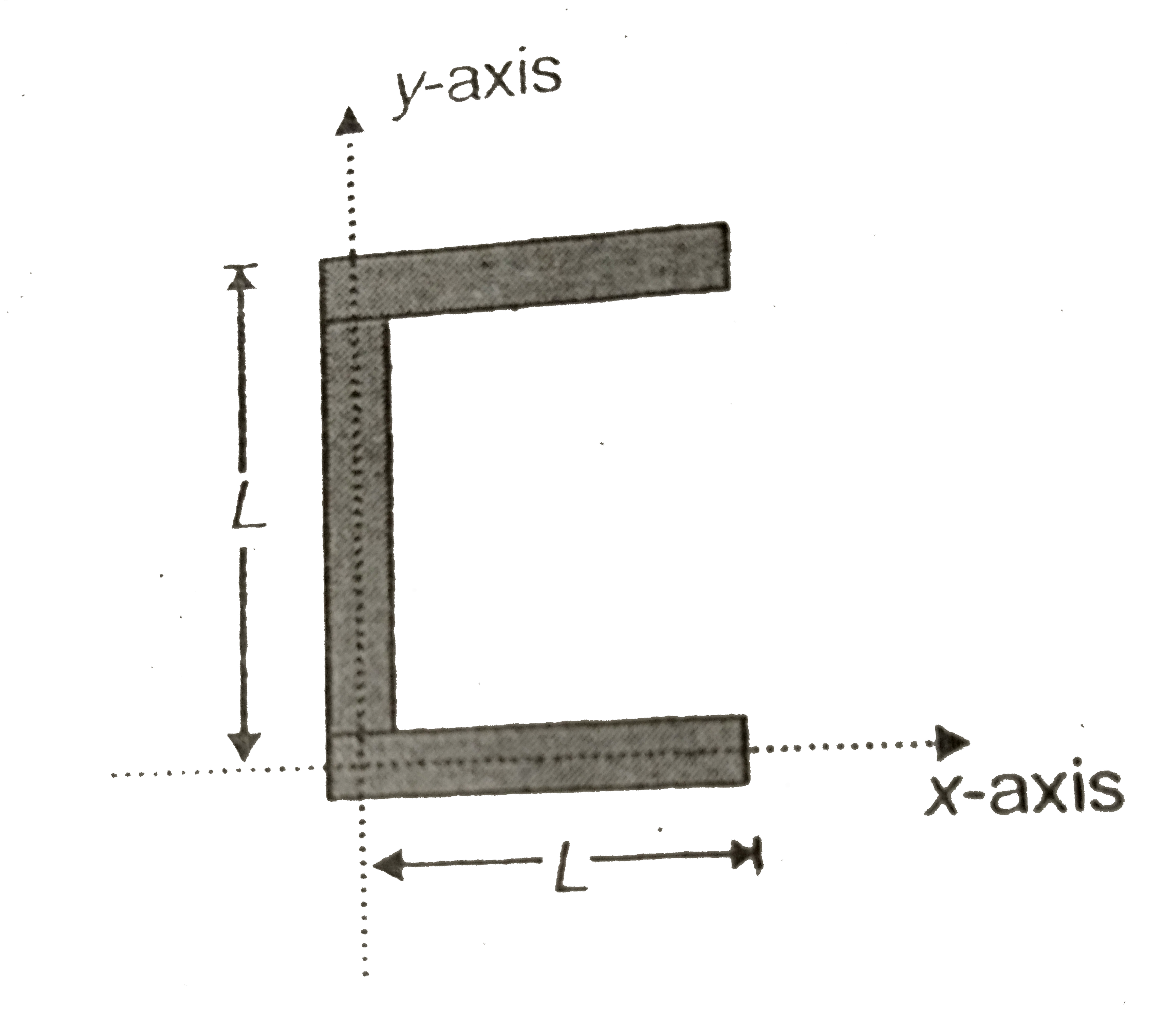
Two identical uniform rods AB and CD, each of length L are jointed to form a T-shaped frame as sown in figure. Locate the centre of mass of the frame. The centre of mass of a uniform rod is at the middle point of the rod.

Video Solution
Text Solution
Let the mass of each rod be m. Tke the centre C of the rod AB as the origin andCB as the Y-axis. The rod AB hs mass m and its centre of mass is at C. For the calculation of the centre of mass of the combined system, AB may be replaced by a point particle of mass m placed at the piont C. Similarly the rod CB may be replaced by a point particle of mas m placed at teh centre E of the rod CD. Thus the framed is equivalent to a system of two particles of equal masses m each, placed at C and E. The centre of mass masses m each, placed at C and E. Teh centre of mass of this pair of particles will be at the middle point F of CE.
The centre of mass of the frame is therefore, on the rod CD at a distance L/4 from C.
|
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - worked out Examples
23 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Short Answer
25 Videos
- CALORIMETRYBOOK - HC VERMACHAPTER - CALORIMETRYEXERCISE - Exercises
18 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
Similar Questions
Knowledge Check
Two identical thin uniform rods of length L each are joined to form T shape as shown in the figure. The distance of centre of mass from D is
 A0BL/4C3L/4DL
A0BL/4C3L/4DLTwo uniform thin identical rods AB and CD each of mass M and length L are joined so as to form as cross as shown. The monent of inertia of the cross about a bisector line EF is
 AML26BML24CML212DML23
AML26BML24CML212DML23Two uniform thin identical rods AB and CD each of mass M and length L are joined so as to form a cross as shown. The moment of inertia of the cross about a bisector line EF is :-
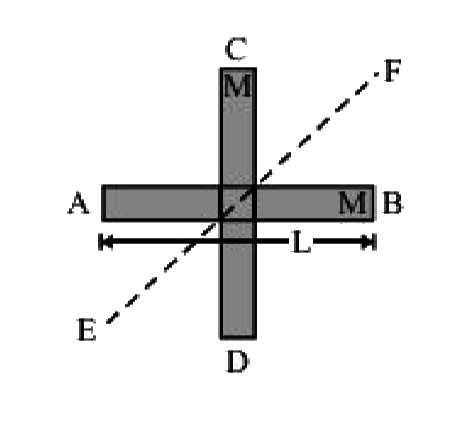 AML26BML24CML212DML23
AML26BML24CML212DML23
Show that the centre of mass of uniform rod of mass M and length L lies at the middle point of the rod.
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

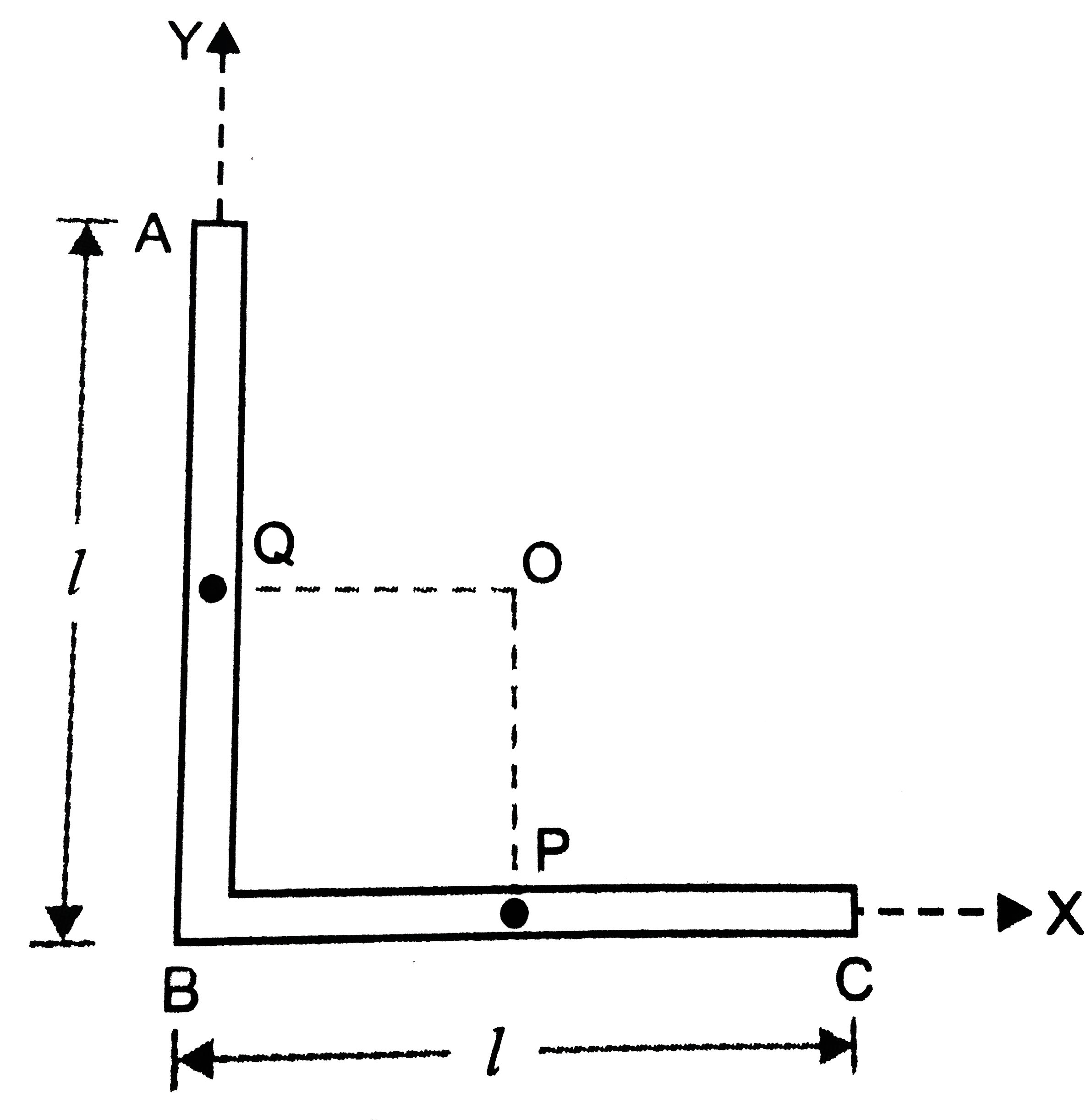
View SolutionA rod of length 2l is bent as shown in figure. Coordinates of centre of mass are
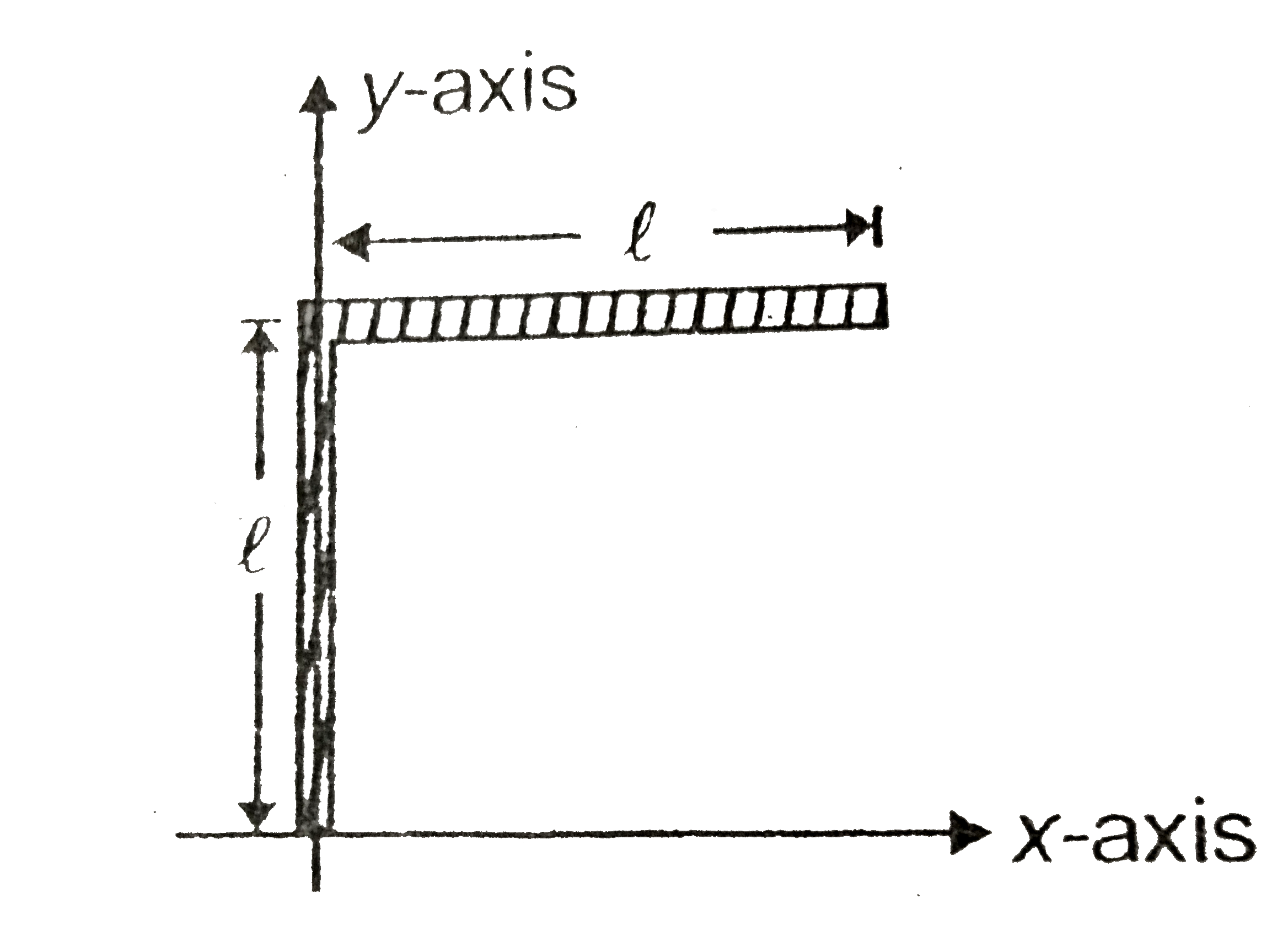
View SolutionLocate the centre of mass of arrangement shown in figure. The three rods are identical in mass and length
View SolutionA uniform thin rod is bent in the form of closed loop ABCDEFA as shown in the figure. The y− coordinate of the centre of mass of the system is
View Solution