Two immiscible liquids of densities ρ and 2ρ and thickness (heights) h and 2h, respectively, push a vertical plate. Find the total side thrust given by the liquids on the vertical plate.

The correct Answer is:F=132ρgh2b
Let the hydrostatic forces acting on the rectangular pathes of areas A1 and A2 of the gate be F1 and F2. Then the total hydrostatic force on the gate is
F=F1+F2
where F1=Pav1A1 and F2=Pav2A2.Pav1 and Pav2 and Pav2 are the average pressures on areas A1 and A2, respectively.
F=Pav1A1+Pav2A2
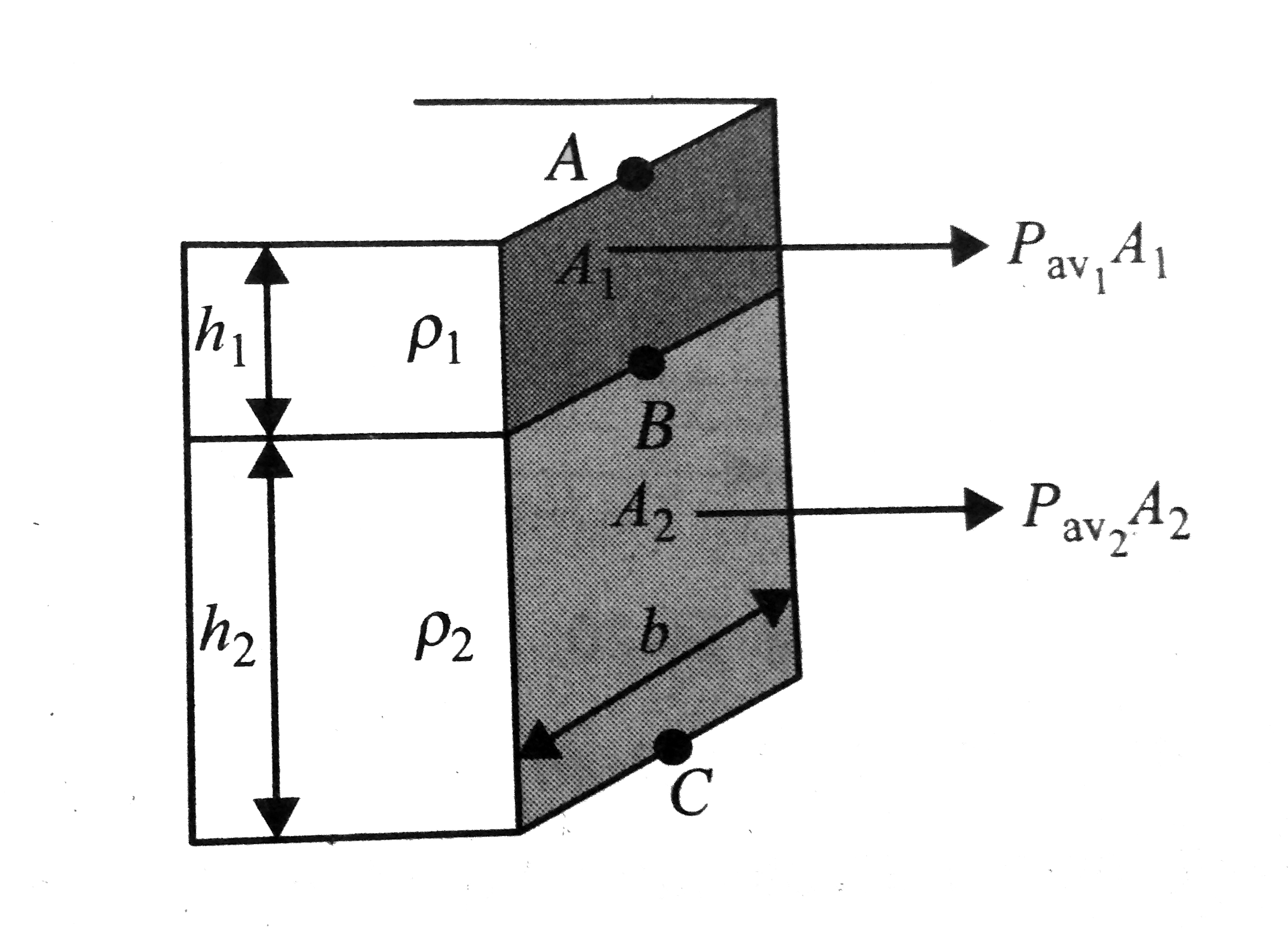
Substituting Pav1=(PA+PB)/2,A1=bh1=bh,Pav2=(PB+PC).2,A2=bh2=b(2h), we have
F=(PA+PB)2bh+(PB+PC)22bh
Substituting PA=0,PB=ρgh and PC=(ρ1h1+ρ2h2)g=[ρh+(2ρ)(2h)]=5ρgh, we have
F=32ρgh2b
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Single Correct
95 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.4
10 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A thin triangular glass tube containing immiscible liquids A, B, C of densities ρ,2ρ,3ρ is at rest in vertical plane. Find x.

View SolutionTwo non-viscous, incomoressible and immiscible liquids of densities ρ and 1.5ρ are poured into the two limbs of a circules tube of radius R and small cross-section kept fixed in a vertical plane as shown in fig. Each liquid occupies one-fourth the cirumference of the tube.

(a) Find the angle θ the radius to the interface makes with the vertical in equilibrium position.
(b) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations alre simple harmonic. Find the time period of these oscillations.
View Solution
Knowledge Check
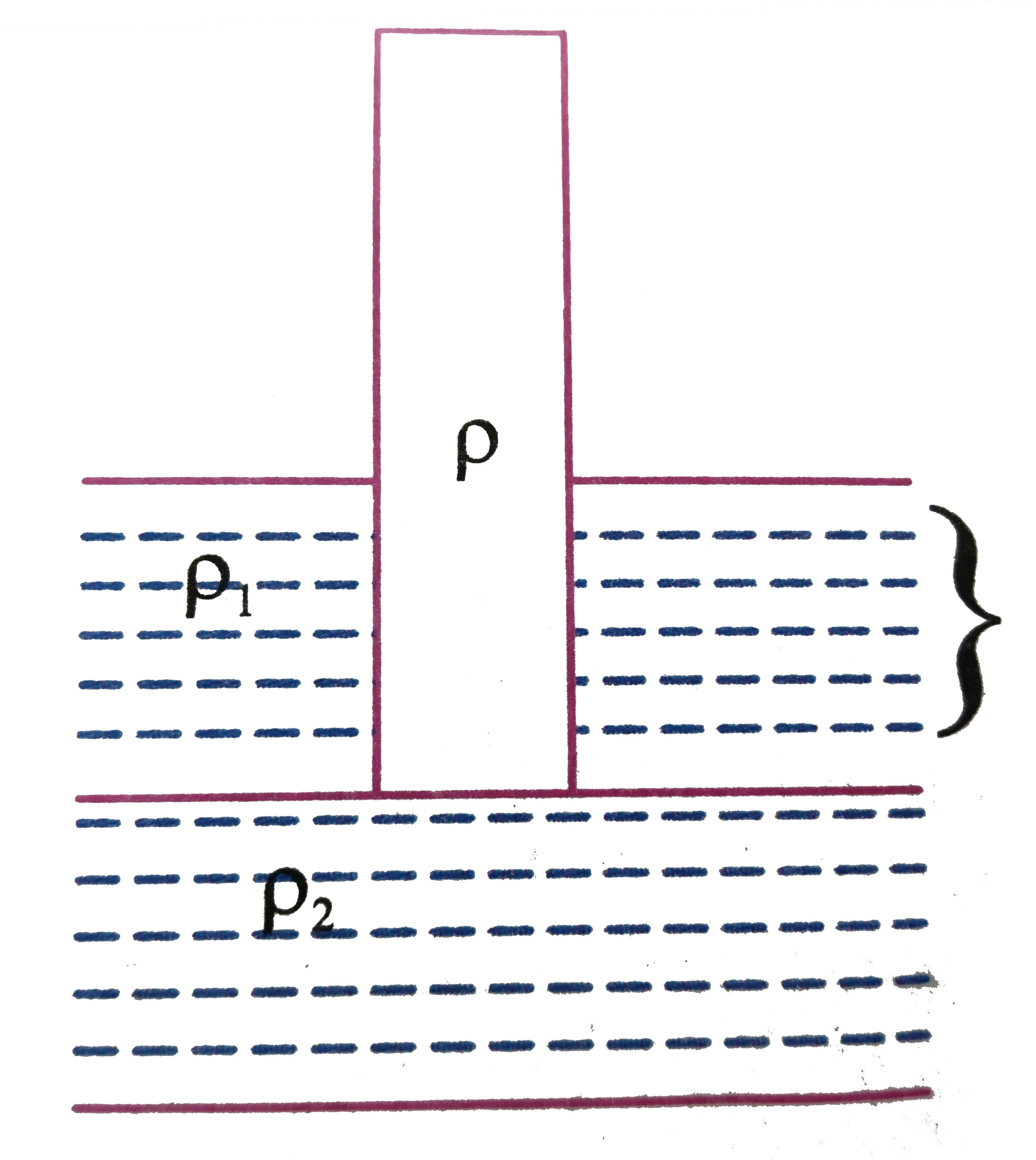
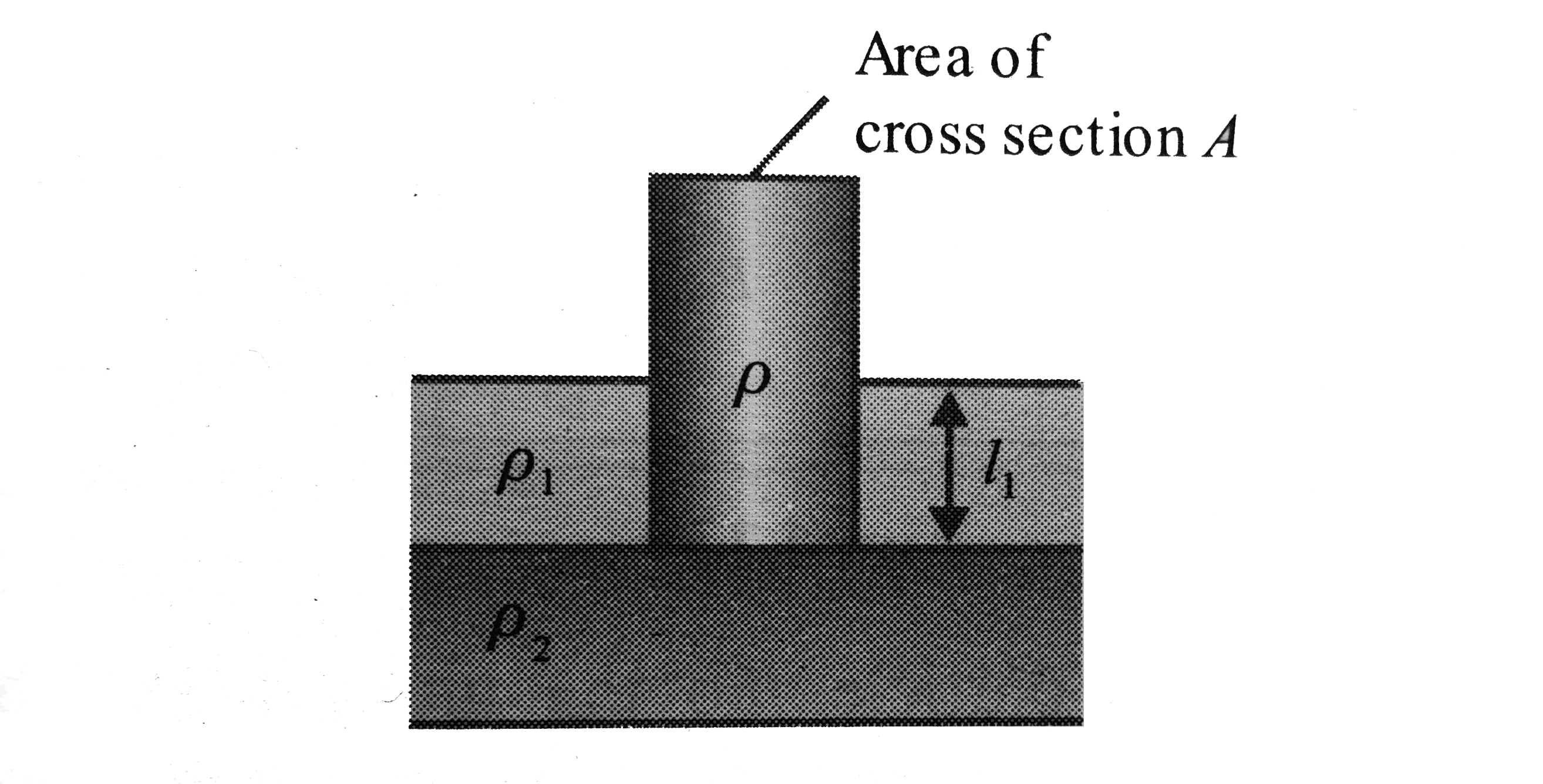
A vertical pole of length l, density ρ, area of cross section A, floats in two immiscible liquids of densities ρ1 and ρ2. In equilibrium position the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, the time period of oscillation is..........
 Aπ√ρl(ρ1+ρ2)gBπ√ρlg(1√ρ1+1√ρ2)Cπ√(ρ1+ρ2)lρgDπ√lρg(√ρ1+√ρ2)
Aπ√ρl(ρ1+ρ2)gBπ√ρlg(1√ρ1+1√ρ2)Cπ√(ρ1+ρ2)lρgDπ√lρg(√ρ1+√ρ2)Equal volume of two immiscible liquids of densities ρ and 2ρ are filled in a vessel as shown in the figure. Two small holes are punched at depths h/2 and 3h/2 from the surface of lighter liquid. If v1 and v2 are the velocities of efflux at these two holes, then v1/v2 is
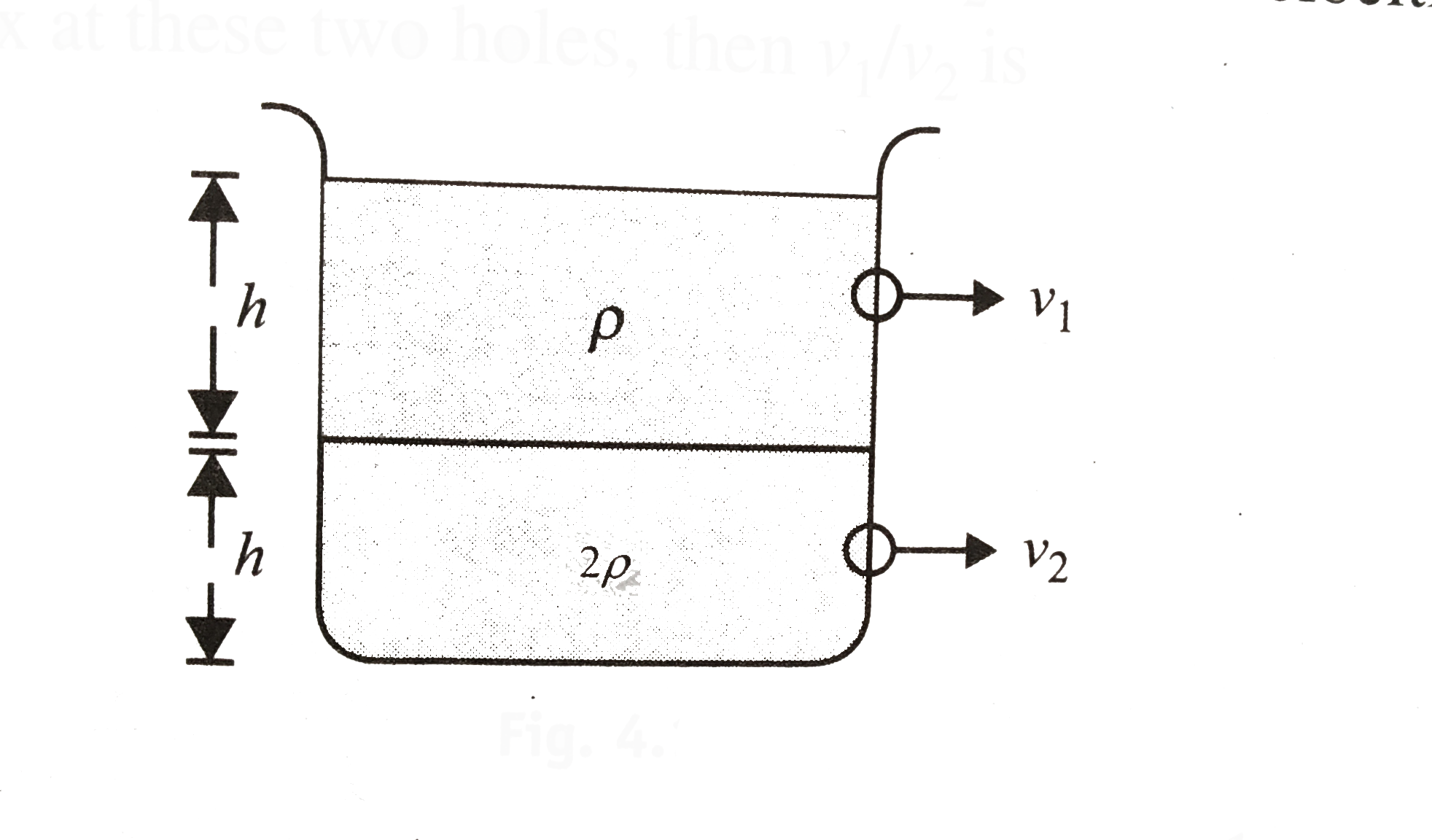 A12√2B12C14D1√2
A12√2B12C14D1√2In a cylindrical vessel containing liquid of density ρ, there are two holes in the side walls at heights of h1 and h2 respectively such that the range of efflux at the bottom of the vessel is same. The height of a hole, for which the range of efflux would be maximum, will be –
 Ah2−H1BH2+H2C⋅h2−h2)2Dh2+h12
Ah2−H1BH2+H2C⋅h2−h2)2Dh2+h12
A vertical pole of length l , density ρ , area of cross section A floats in two immiscible liquids of densities ρ1and ρ2. In equuilibrium possition the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, find the time period of oscillation.
View SolutionTwo liquids of densities ρ and 3rho having volumes 3V and V are mixed together. Find density of the mixture.
View SolutionEqual volumes of two immiscible liquids of densities ρand2ρ are filled in a vessel as shown in figure. Two small holes are punched at depth h/2 and 3h/2 from the surface of lighter liquid. If v1andv2 are the velocities of efflux at these two holes then (v2v1)2 is

View Solution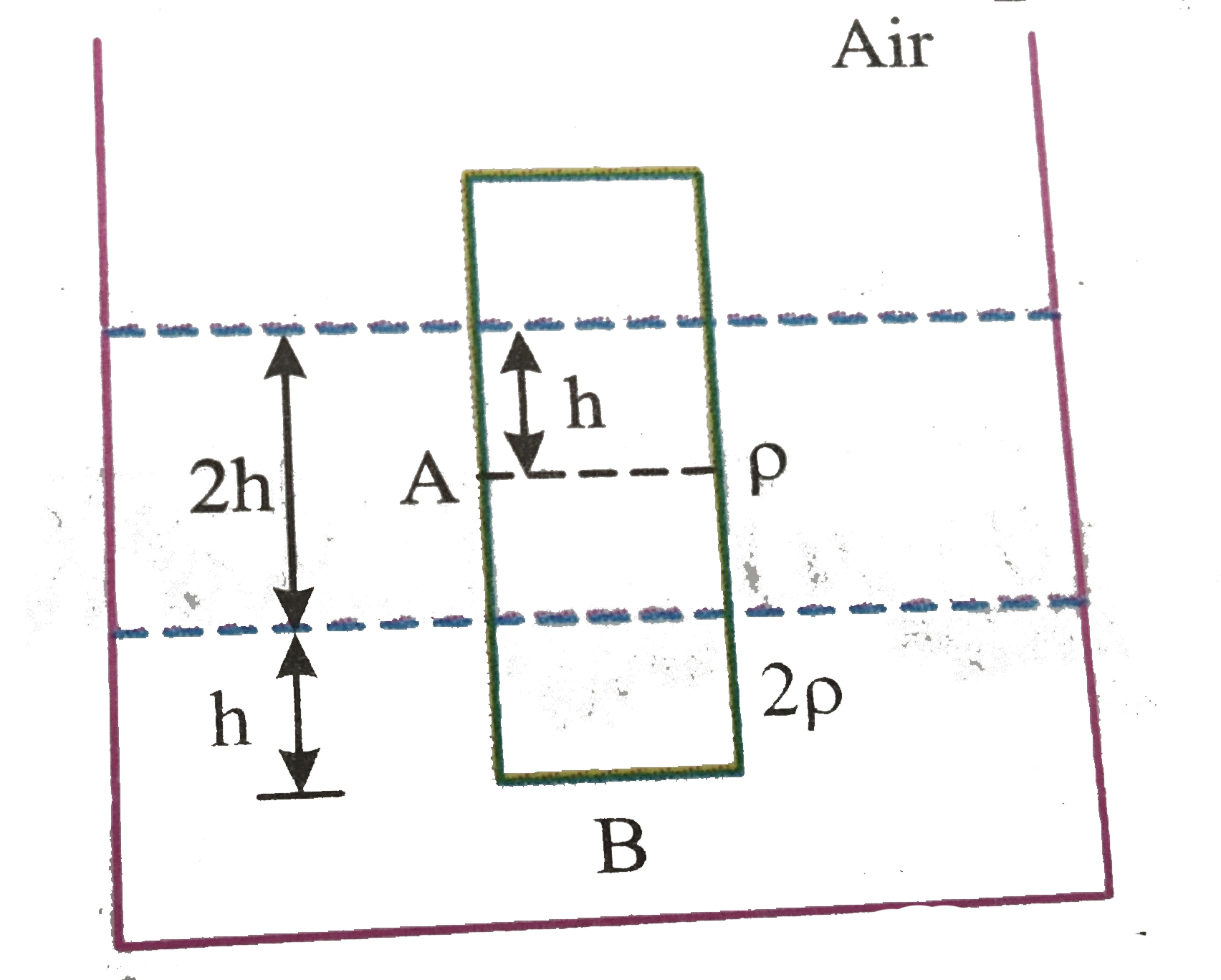
A cylinder stands vertical in two immiscible liquids of densities ρ and 2ρ as shown. Find the difference in pressure at point A and B:
View SolutionA thin uniform tube is bent into a circle of radius r in the vertical plane. Equal volumes of two immiscible liquids, whose densities are ρ1 and ρ2(ρ1>ρ2) fill half the circle. The angle θ between the radius vector passing though the common interface and the vertical is :
View Solution
