Two masses m1 and m2 are connected by a light string passing over a smooth pulley. When set free m1 moves downward by 2 m in 2 s. The ratio m1/m2 is
9/7
11/9
13/11
15/13
The correct Answer is:B
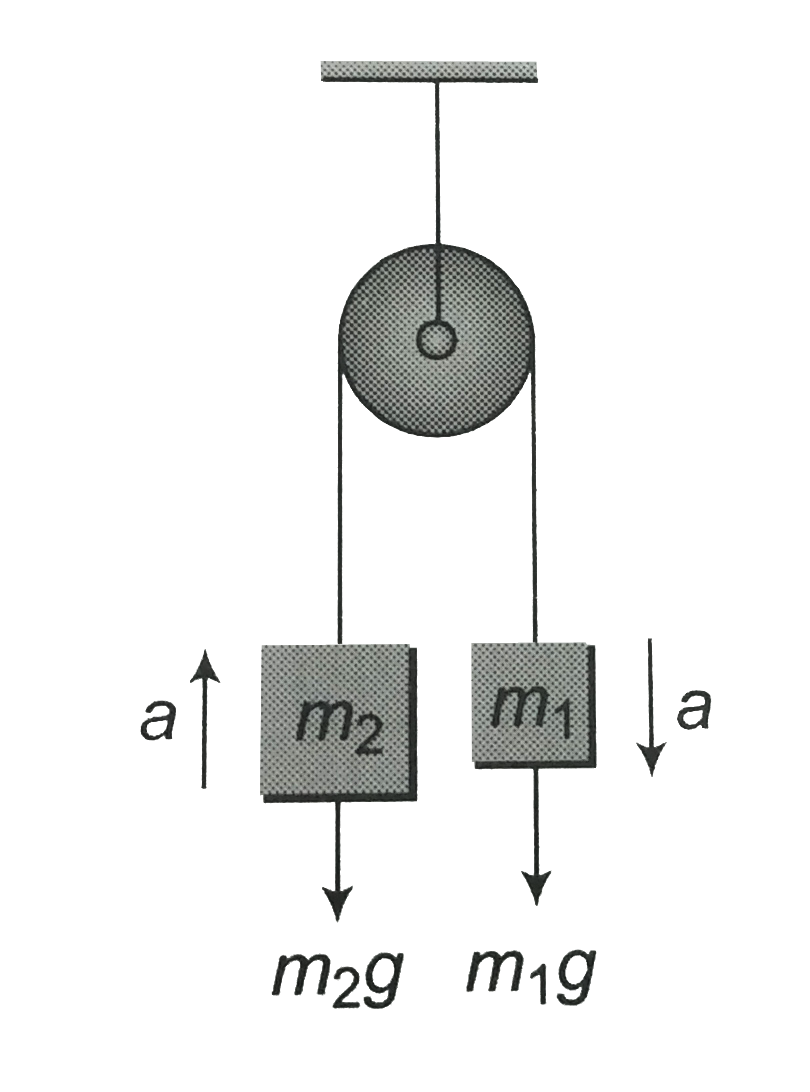
a=(m1−m2)g(m1+m2)
x=12at2
2=12a(2)2
a=1m/s2
(m1−m2)g(m1+m2)=1
10m1−10m2=m1+m2
9m1=11m2
m1m2=119
Topper's Solved these Questions
Similar Questions
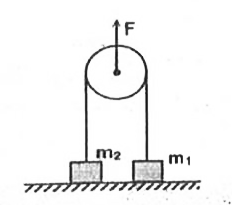
Two masses m1andm2 are connected by means of a light string, that passes over a light pulley as shown in the figure. If m1=2kgandm2=5kg and a vertical force F is applied on the pulley, then find the acceleration of the masses and that of the pulley when
(a) f = 35N, (b) F = 70N, (c) F = 140N.
 View Solution
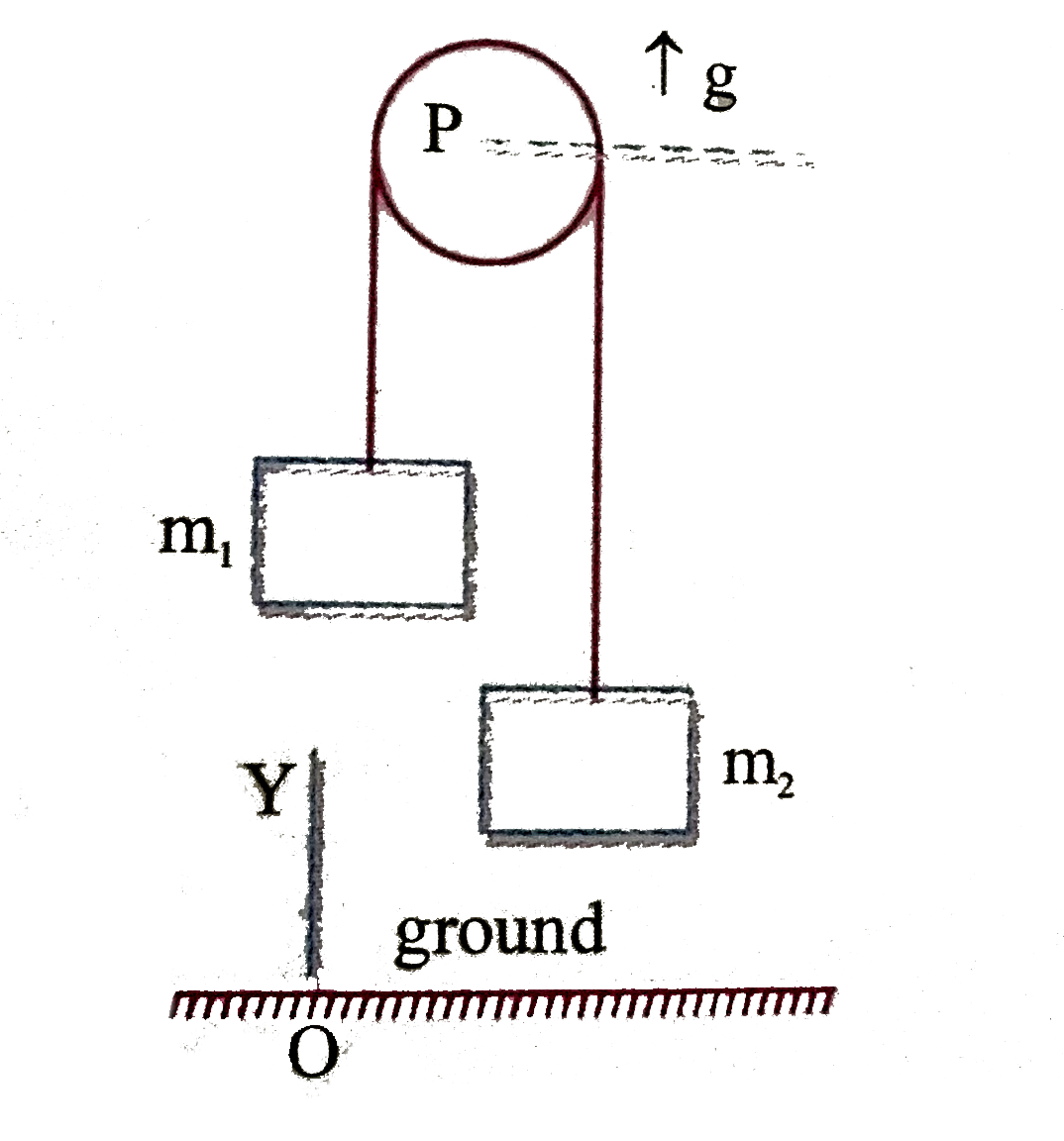
View SolutionTwo masses m1 and m2 are connected by light inextensible string passing over a smooth pulley P. If the pulley moves vertically upwards with an acceleration equal to g then
 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One or More
Two masses M and m(M>m) are joined by a light string passing over a smooth light pulley.
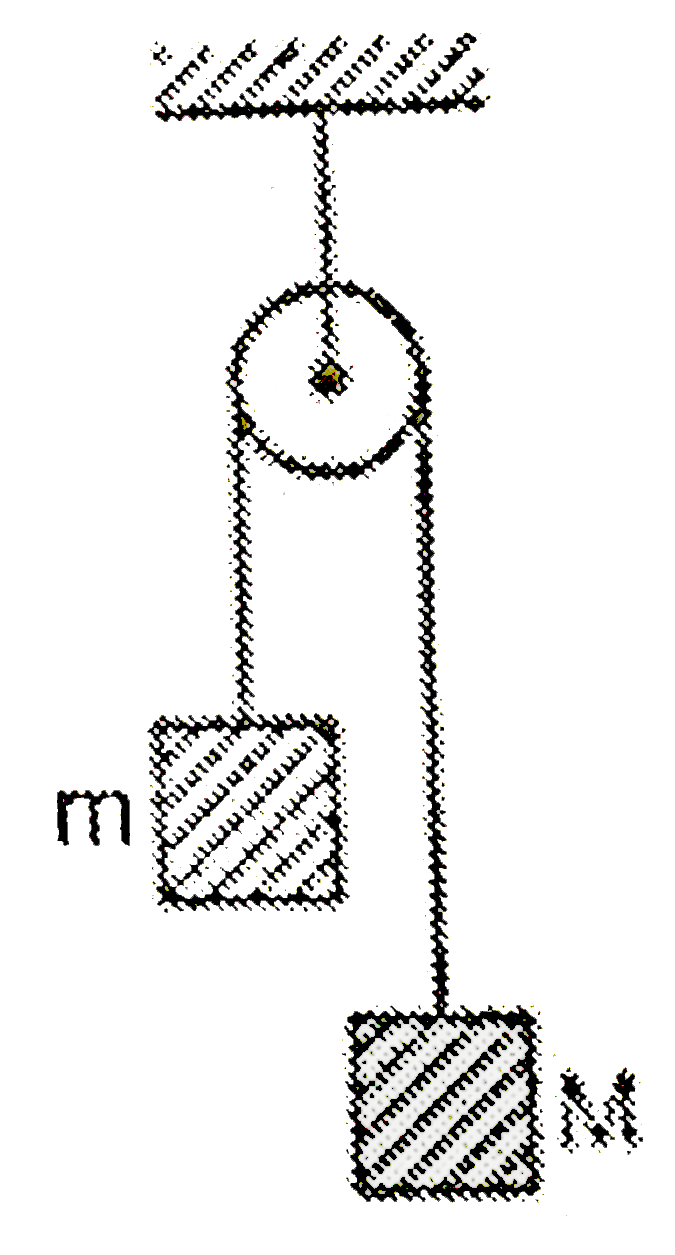 AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g
AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g - Question 2 - Select One or More
Two masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
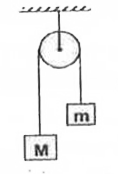 Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above
Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above - Question 3 - Select One
Two masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration
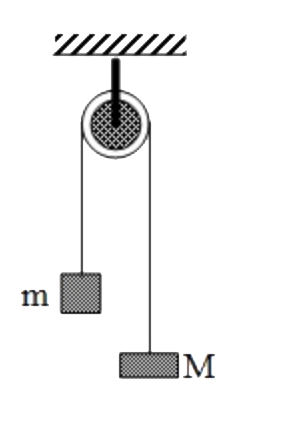 Ag(M−mM+m) downwardBg(M−mM+m)2 downwardCg(M−mM+m)2 upward if M<mDzero
Ag(M−mM+m) downwardBg(M−mM+m)2 downwardCg(M−mM+m)2 upward if M<mDzero
Two bodies of masses m1andm2 are connected by a light string going over a smooth lilght pulley at the end of an incline. The mass1 lies on the incline m2 hangs vertically. The system is t rest. Find the angle of the incline and the fore exerted by the incline on the body of mass m_1.
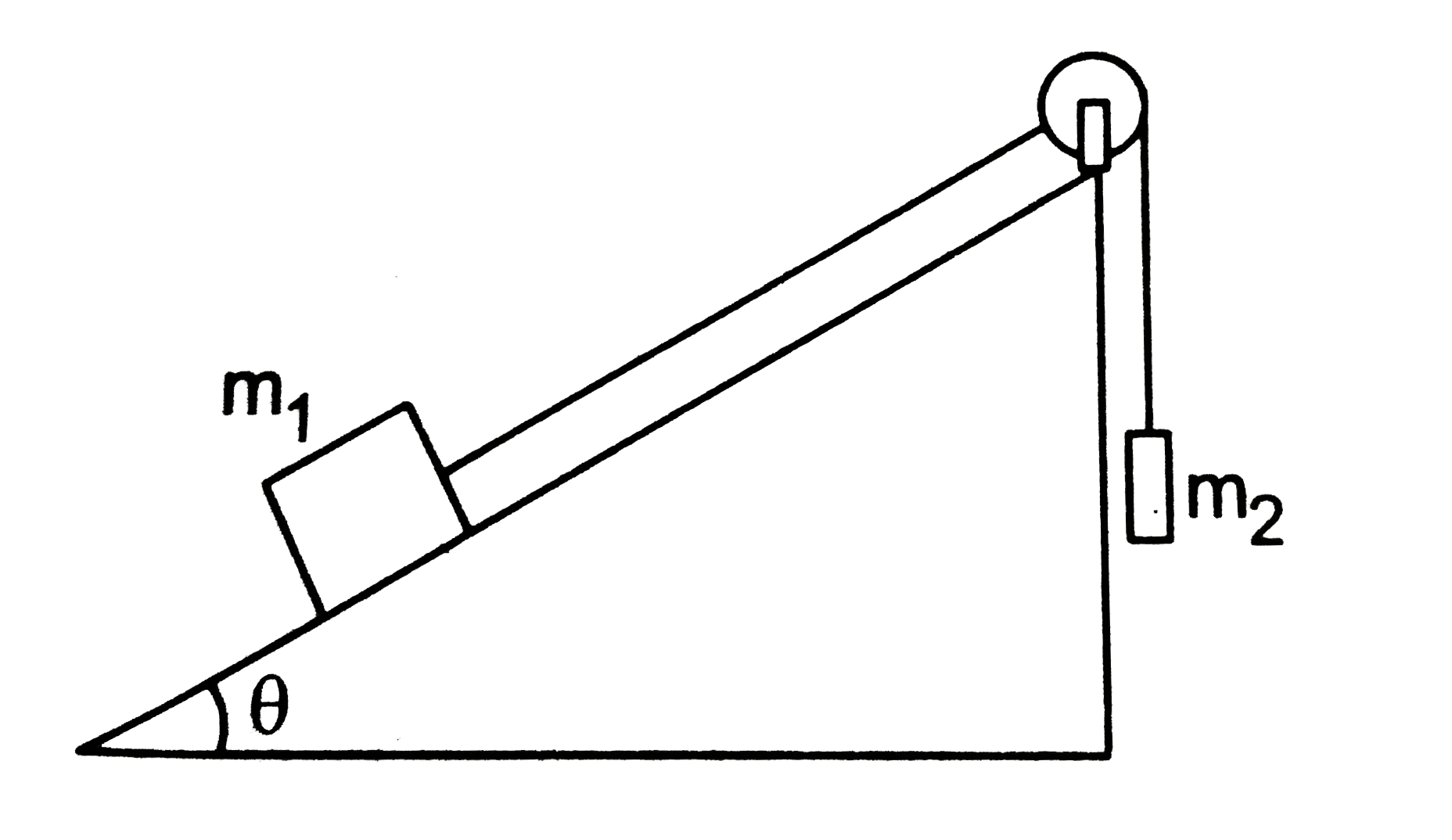 View Solution
View SolutionTwo masses m1andm2 are connected to the end of a string passing over a smooth pulley . The magnitude of tension in the string is T and the masses are moving with magnitude of acceleration a . If the masses are interchanged , then
View SolutionTwo bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
View SolutionConsider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
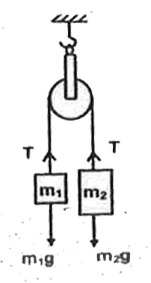
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
If the pulley is pulled upward with acceleration equal to the acceleration due to gravity, what will be the tension in the string?View SolutionConsider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
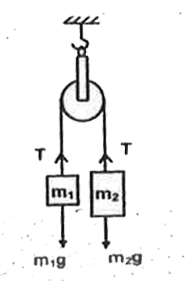
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
What is the tension in the string?View Solution

