Two masses m1andm2 re connected by a spring of spring constant k and are placed on as frictionless horizontal surface. Initially the spring is stretched through a distance x0 when the system is released from rest. Find the distance moved by the two masses before they again come to rest.
To solve the problem of two masses m1 and m2 connected by a spring with spring constant k on a frictionless surface, we need to determine the distance moved by the two masses before they come to rest again after being released from an initial stretch x0.
1. Understand the Initial Setup:
- The two masses m1 and m2 are connected by a spring that is initially stretched by a distance x0.
- The natural length of the spring is L0, so the initial length of the spring when stretched is L0+x0.
2. Release from Rest:
- When the system is released from rest, the spring will exert forces on both masses, causing them to move.
3. Final Condition:
- The masses will come to rest again when the spring is compressed by the same amount x0. Thus, the final length of the spring will be L0−x0.
4. Calculate the Total Movement:
- The total change in length of the spring from its initial stretched position to its final compressed position is:
ΔL=(L0+x0)−(L0−x0)=2x0
- This means that the total distance moved by both masses combined is 2x0.
5. Displacement of Each Mass:
- Let x1 be the displacement of mass m1 and x2 be the displacement of mass m2.
- The relationship between the displacements is given by the conservation of momentum and the center of mass remaining stationary:
m1x1+m2x2=0
- This implies:
m1x1=−m2x2orx1=−m2m1x2
6. Sum of Displacements:
- The total displacement is:
x1+x2=2x0
- Substituting x1 in terms of x2:
−m2m1x2+x2=2x0
- Factoring out x2:
x2(1−m2m1)=2x0
7. Solving for x2:
- Rearranging gives:
x2=2x01+m2m1=2x0m1m1+m2
8. Finding x1:
- Using the relationship x1=−m2m1x2:
x1=−m2m1⋅2x0m1m1+m2=−2m2x0m1+m2
Final Result:
- The distances moved by the masses before they come to rest again are:
- Mass m1 moves x1=2m2x0m1+m2
- Mass m2 moves x2=2m1x0m1+m2
- The two masses m1 and m2 are connected by a spring that is initially stretched by a distance x0.
- The natural length of the spring is L0, so the initial length of the spring when stretched is L0+x0.
- When the system is released from rest, the spring will exert forces on both masses, causing them to move.
- The masses will come to rest again when the spring is compressed by the same amount x0. Thus, the final length of the spring will be L0−x0.
- The total change in length of the spring from its initial stretched position to its final compressed position is:
ΔL=(L0+x0)−(L0−x0)=2x0
- This means that the total distance moved by both masses combined is 2x0.
- Let x1 be the displacement of mass m1 and x2 be the displacement of mass m2.
- The relationship between the displacements is given by the conservation of momentum and the center of mass remaining stationary:
m1x1+m2x2=0
- This implies:
m1x1=−m2x2orx1=−m2m1x2
- The total displacement is:
x1+x2=2x0
- Substituting x1 in terms of x2:
−m2m1x2+x2=2x0
- Factoring out x2:
x2(1−m2m1)=2x0
- Rearranging gives:
x2=2x01+m2m1=2x0m1m1+m2
- Using the relationship x1=−m2m1x2:
x1=−m2m1⋅2x0m1m1+m2=−2m2x0m1+m2
- The distances moved by the masses before they come to rest again are:
- Mass m1 moves x1=2m2x0m1+m2
- Mass m2 moves x2=2m1x0m1+m2
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Question For short Answer
25 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -1
18 Videos
- CALORIMETRYBOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer
9 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
Similar Questions
Two blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of oscillation is
View SolutionTwo blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionTwo uniform discs A and B of equal radii but having different masses 1 kg and 2 kg respectively, are connected (at centres) by a massless spring of spring constant k=1000Nm−1 and then placed on a sufficiently rough horizontal surface. If initially, the system is released from rest with the spring being compressed by 10 cm, then the speed of A when the spring comes back to its natural length, is

View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of spring
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.
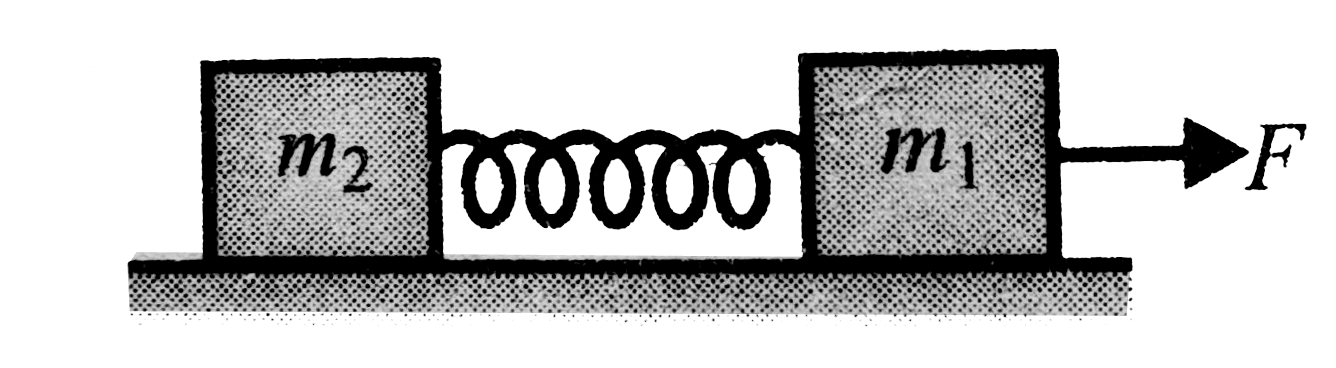
Which of the following statement is not true tn the watt of above system.
View SolutionTwo blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is

View SolutionTwo bars of masses m1 and m2 connected by a weightless spring of stiffness k, rest on a smooth horizontal plane. Bar 2 is shifted by a small distance x0 to the left and released. The veloicyt of the centre of mass of the system when bar 1 breaks off the wall is
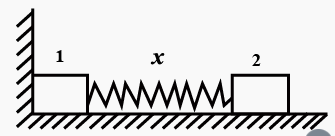
View SolutionTwo blocks, of masses M and 2M, are connected to a light spring of spring constant K that has one end fixed, as shown in figure. The horizontal surface and the pulley are frictionless. The blocks are released from when the spring is non deformed. The string is light.
 .
.
View Solution
