Two metal spheres of capacitances C1andC2carry some charges . They are put in contact and then seperated.The final charges Q1andQ2 on them will satisfy
Q1Q2<C1C2
Q1Q2=C1C2
Q1Q2>C1C2
Q1Q2=C2C1
The correct Answer is:B
To solve the problem step by step, we need to analyze the situation of two metal spheres with capacitances C1 and C2 that are put in contact and then separated.
Step 1: Understanding the Initial Conditions
Initially, the two metal spheres have charges Q1 and Q2 and their respective capacitances are C1 and C2. The potentials of the spheres can be expressed as:
V1=Q1C1andV2=Q2C2
Step 2: Contacting the Spheres
When the spheres are brought into contact, charge will flow between them until they reach the same potential. This is because charge flows from a region of higher potential to a region of lower potential. Therefore, we set the potentials equal:
V1=V2
Step 3: Setting the Potentials Equal
From the expressions for the potentials, we have:
Q1C1=Q2C2
Step 4: Rearranging the Equation
Cross-multiplying gives us:
Q1⋅C2=Q2⋅C1
Step 5: Expressing the Charge Ratio
We can rearrange this equation to express the ratio of the charges:
Q1Q2=C1C2
Conclusion
Thus, the final charges Q1 and Q2 on the spheres after they are separated will satisfy the relationship:
Q1Q2=C1C2
Final Answer
The final charges Q1 and Q2 will satisfy the equation Q1Q2=C1C2.
---
Initially, the two metal spheres have charges Q1 and Q2 and their respective capacitances are C1 and C2. The potentials of the spheres can be expressed as:
V1=Q1C1andV2=Q2C2
When the spheres are brought into contact, charge will flow between them until they reach the same potential. This is because charge flows from a region of higher potential to a region of lower potential. Therefore, we set the potentials equal:
V1=V2
From the expressions for the potentials, we have:
Q1C1=Q2C2
Cross-multiplying gives us:
Q1⋅C2=Q2⋅C1
We can rearrange this equation to express the ratio of the charges:
Q1Q2=C1C2
Thus, the final charges Q1 and Q2 on the spheres after they are separated will satisfy the relationship:
Q1Q2=C1C2
The final charges Q1 and Q2 will satisfy the equation Q1Q2=C1C2.
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE 2
6 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - Exercise
65 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - worked out examples
23 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
Similar Questions
Knowledge Check
Metallic sphere of radius R is charged to potential V. Then charge q is proportional to
AVBRCboth V and RDnone of these
Consider three identical metal spheres A,B and C. Sphere A carries charge +6q, sphere B carries charge −3q and sphere C carries no charge . Spheres A and B are touched together and then separated. Sphere C is then touched to sphere A and separated from it . Finally the sphere C is touched to sphere B and separated from it . Find the final charge on the sphere C.
View SolutionCharges q1 , q2 and q3 are placed on capacitors of capacitance C1, C2 and C3, respectively, arranged in series as shown. Switch S is there closed. What are the final charges q'1, q'2 and q'3 on the capacitors?
Given q1=30μC, q2=μC, q3=10μC, C1=10μF, C2=20μF, C3=30μF and ε=12volt
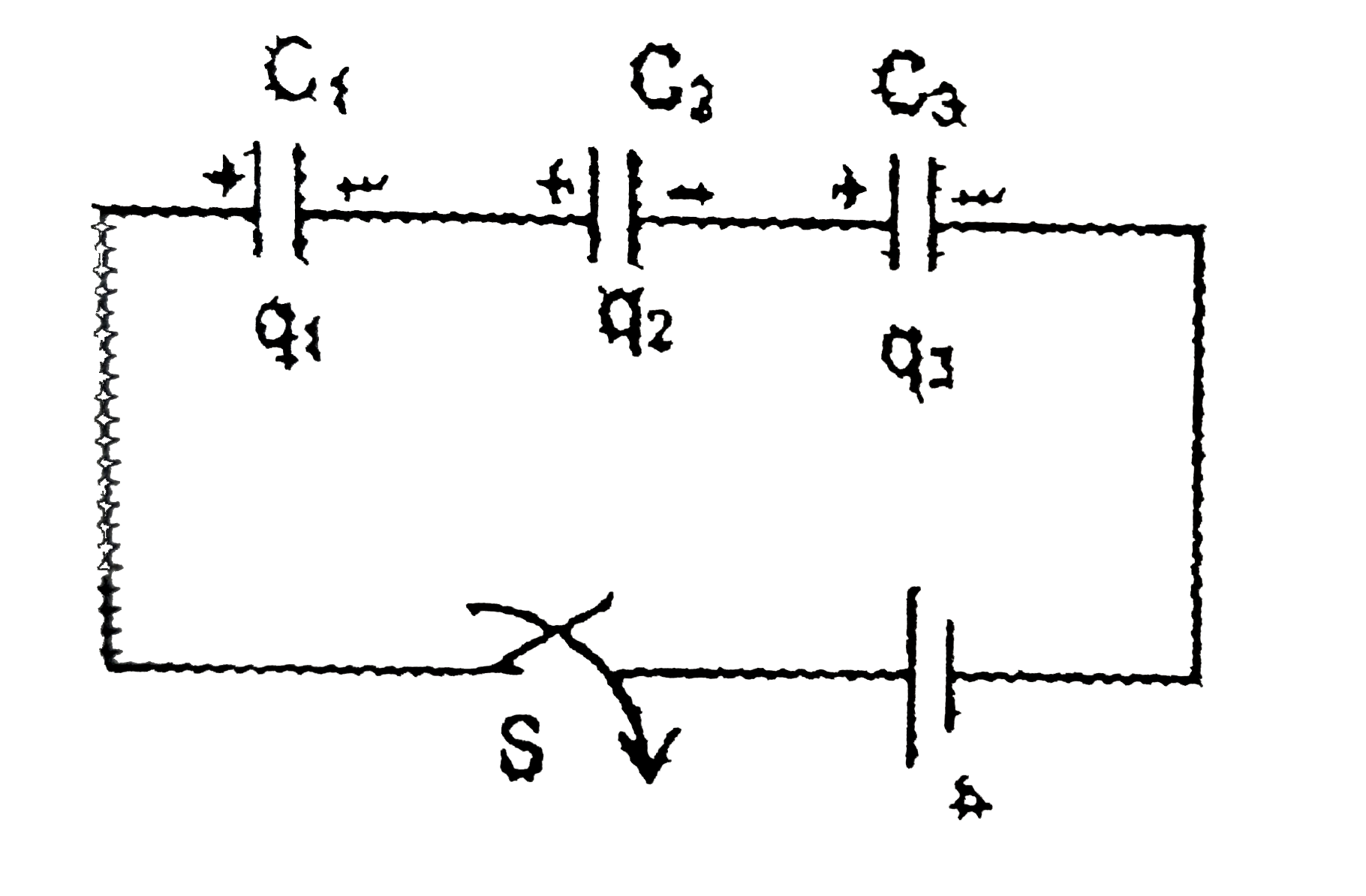
View SolutionTwo metallic spheres of radii 1cm and 2cm are given charges 10−2C and 5×10−2C respectively. If they are connected by a conducting wire, the final charge on the smaller sphere is
View SolutionA solid metal sphere of radius R has a charg +2Q. A hollow spherical shell of radius 3R placed concentric with the frist sphere has net charge -Q.
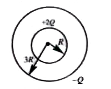
What would be the final distribution of charges if the sphres are joined by a conducting wire
View SolutionA charge Q is placed at the centre of an uncharged, hollow metallic sphere of radius alpha. (a) Find the surface charge density on the inner surface and on the outer surface. (b) If a charge q is put on the sphere, what would be the surface charge densities on the inner and the outer surface?
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View Solution

