Two parallel beams of protons and electrons, carrying equal currents are fixed at a separation d. The protons and electrons move in opposite directions. There is a point P on the straight perpendicular line joining the two beams at a distance x from one beam. The magnetic field at this point is B. If B is plotted against x, it can be represented by the curve.
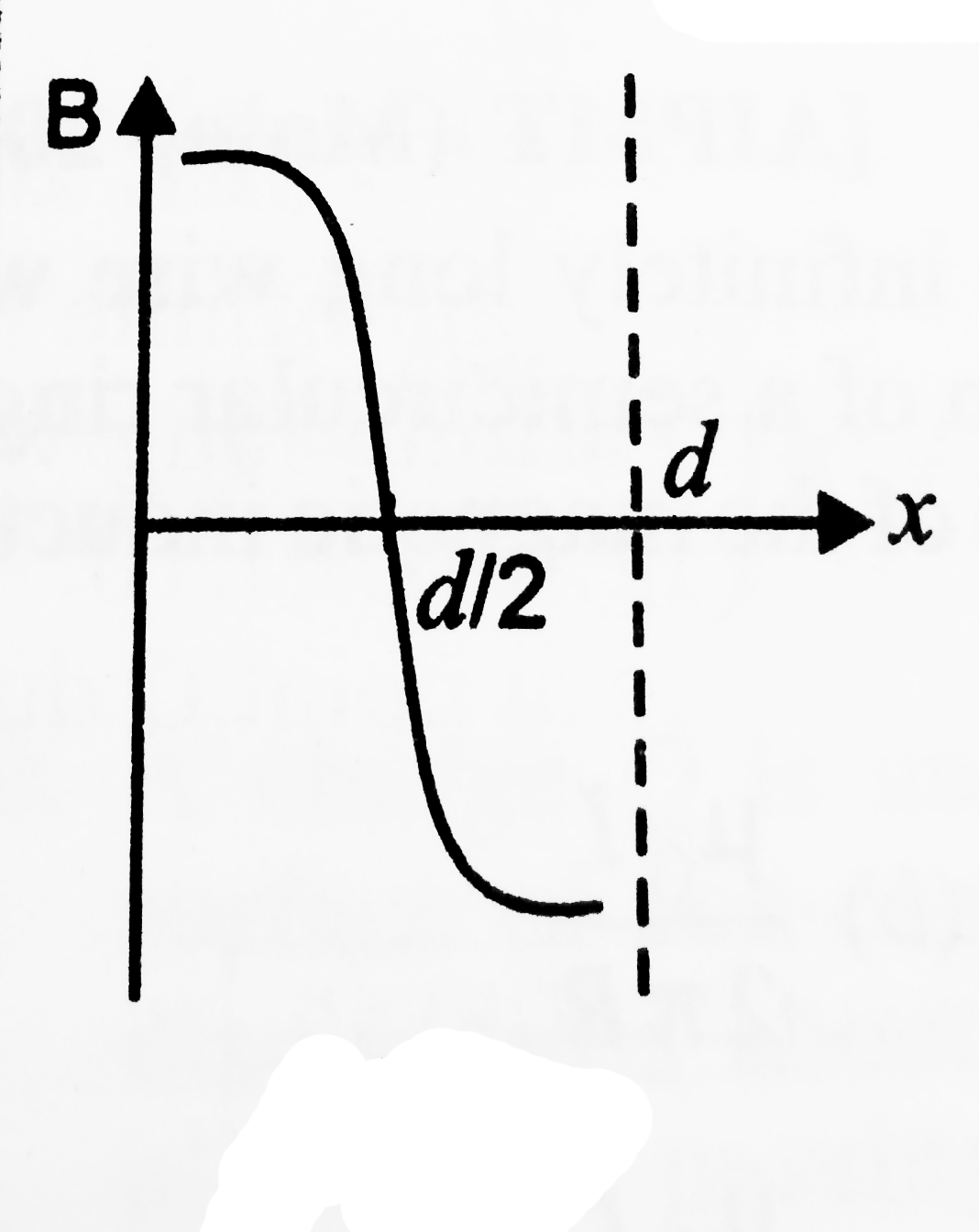
The correct Answer is:B
The two parallel beams of protons and electrons will be equivalent to two linear parallel line wires carrying currents in the same direction. The resultant magnetic field at P is
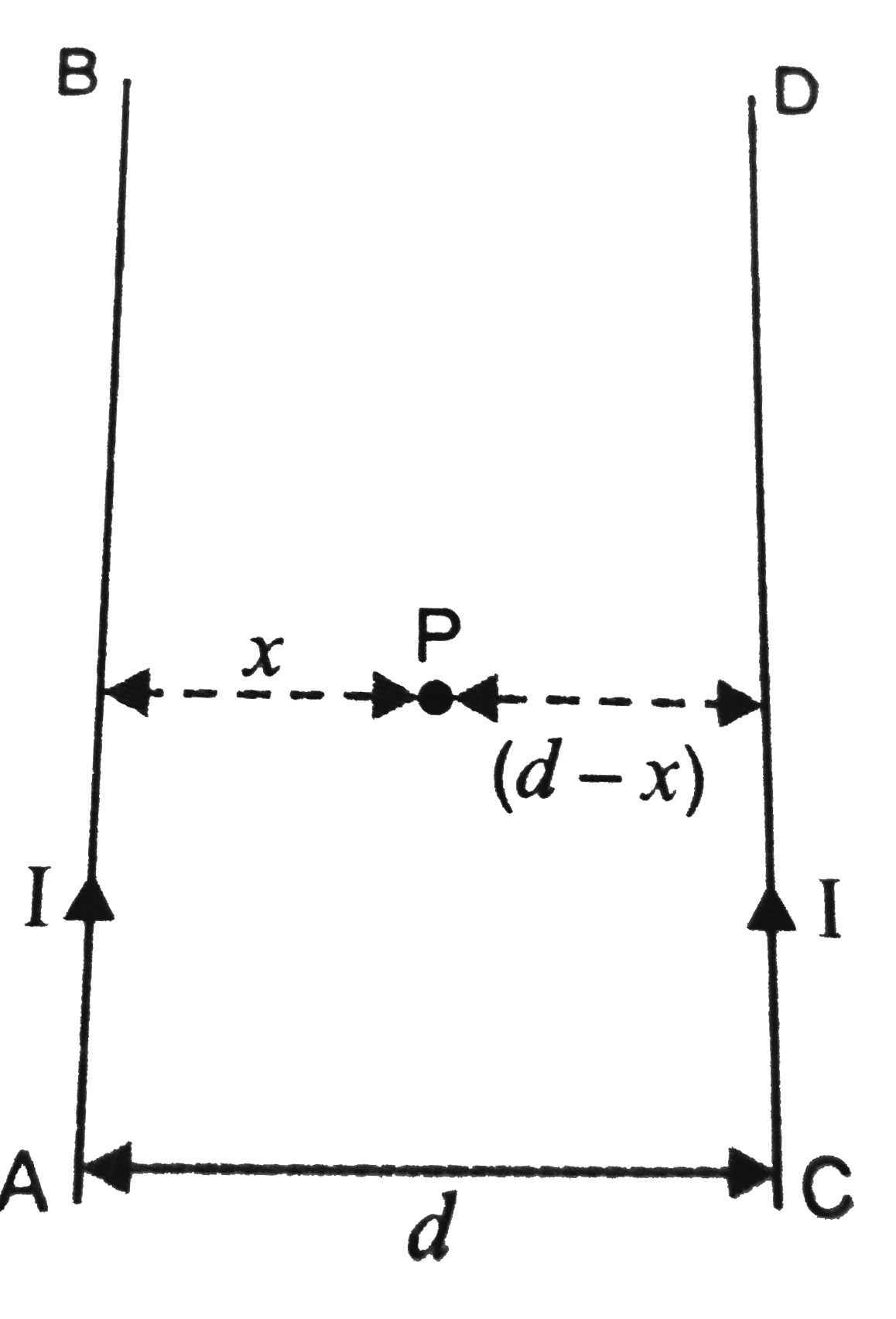
B=μ04π2Ix−μ04π2I(d−x)=μ04π2I[1x−1d−x]
If x=d/2, B=0. If x<d/2, B is positive and if x>d/2 then B is negative. Thus variation between B and x will be represented by option (b).
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (a)1videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (c)1videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Value Based Questions2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS2videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Multiple choice questions1videos
OPTICS
Similar Questions
A and B are two conductors carrying a current i in the same direction x and y are two electron beams moving in the same direction. There will be
View SolutionA and B are two conductors carrying a current i in the same direction x and y are two electron beams moving in the same direction. There will be
View Solution
Knowledge Check
- Question 1 - Select One
Two parallel beams of protons and electrons, carrying equal currents are fixed at a separation d. The protons and electrons move in opposite directions. P is a point on a line joining the beams , at a distacne x from any one beam. The magnetic field at P is B . If B is plotted against x, which of the following best represents the resulting curve
A
B##DPP_PHY_MEI_2_1_E01_099_O02.png" width="30%">C
D
- Question 2 - Select One
Two long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
Aμ0idπ(d2+x2)Bμ0ixπ(d2−x2)Cμ0ix(d2+x2)Dμ0id(d2+x2) - Question 3 - Select One
Two long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
Aμ0idπ(d2+x2)Bμ0ixπ(d2−x2)Cμ0ix(d2+x2)Dμ0id(d2+x2)
Two electrons are fixed at a seperation of 2d from each other.A proton is placed at the mid point and displaced slightly in a direction perpendicular to line joining the two electrons. Find frequency of oscillation of proton
View SolutionA and B are two conductors carrying a current I in the same direction, X and y are two electron beams moving in the same direction. Then there will be
View SolutionTwo long parallel wires are separated by a distance of 2m. They carry a current of 1A each in opposite direction. The magnetic induction at the midpoint of a straight line connecting these two wires is
View Solutionlet B be the magnetic field at a point between the two conductors, at a distance x from the axis. Let B2 be the magnetic field at a point outside conductor, at a distance 2x from the axis
View SolutionTwo ideantical point charges are placed at a separation of d. P is a point on the line joining the charges, at a distance x from any one charge. The field at P is E,E is plotted against x for value of x from close to zero to slightly less then d. Which of the following represents the resulting curve
View Solution