Two parallel wires carry currents of 20A and 40A in opposite directions. Another wire carrying a current antiparallel to 20A is placed midway between the two wires. The magnetic force on it will be
towards 20 A
towards 40 A
zero
perpendicular to the plane of the currents .
The correct Answer is:B
To solve the problem, we need to analyze the magnetic forces acting on the wire carrying a current of 20A that is placed midway between two other wires carrying currents of 20A and 40A in opposite directions.
1. Identify the Configuration:
- We have three wires:
- Wire 1 (I1) carrying 20A (let's assume it goes upwards).
- Wire 2 (I2) carrying 40A (going downwards).
- Wire 3 (I3) carrying 20A (going upwards), placed midway between Wire 1 and Wire 2.
2. Determine the Magnetic Field due to Each Wire:
- The magnetic field (B) created by a long straight current-carrying wire at a distance (r) from it is given by the formula:
B=μ0I2πr
- For Wire 1 (I1 = 20A) at the position of Wire 3 (midway):
- Distance from Wire 1 to Wire 3 = d/2 (where d is the distance between Wire 1 and Wire 2).
- The direction of the magnetic field due to Wire 1 at the position of Wire 3 (using the right-hand rule) will be into the page.
- For Wire 2 (I2 = 40A) at the position of Wire 3:
- The distance is also d/2.
- The direction of the magnetic field due to Wire 2 at the position of Wire 3 will be out of the page.
3. Calculate the Magnitudes of the Magnetic Fields:
- Let’s denote the distance between Wire 1 and Wire 2 as d. The magnetic field at the position of Wire 3 due to Wire 1 (B1) and Wire 2 (B2) can be calculated as:
B1=μ0⋅202π⋅d2=40μ02πd
B2=μ0⋅402π⋅d2=80μ02πd
4. Determine the Net Magnetic Field at Wire 3:
- Since B1 is into the page and B2 is out of the page, the net magnetic field (B_net) at Wire 3 will be:
Bnet=B2−B1=80μ02πd−40μ02πd=40μ02πd
- The net magnetic field is directed out of the page.
5. Calculate the Magnetic Force on Wire 3:
- The magnetic force (F) on a current-carrying wire in a magnetic field is given by:
F=I⋅L⋅B⋅sin(θ)
- Here, I = 20A (current in Wire 3), L is the length of Wire 3, and θ = 90° (since the current is perpendicular to the magnetic field).
- Therefore, the force on Wire 3 (F3) is:
F3=20A⋅L⋅40μ02πd
- The direction of the force, using Fleming's Left-Hand Rule, will be towards Wire 2 (the 40A wire).
6. Conclusion:
- The net magnetic force on the wire carrying 20A (Wire 3) will be directed towards the wire carrying 40A.
Final Answer:
The magnetic force on the wire carrying 20A will be directed towards the wire carrying 40A.
- We have three wires:
- Wire 1 (I1) carrying 20A (let's assume it goes upwards).
- Wire 2 (I2) carrying 40A (going downwards).
- Wire 3 (I3) carrying 20A (going upwards), placed midway between Wire 1 and Wire 2.
- The magnetic field (B) created by a long straight current-carrying wire at a distance (r) from it is given by the formula:
B=μ0I2πr
- For Wire 1 (I1 = 20A) at the position of Wire 3 (midway):
- Distance from Wire 1 to Wire 3 = d/2 (where d is the distance between Wire 1 and Wire 2).
- The direction of the magnetic field due to Wire 1 at the position of Wire 3 (using the right-hand rule) will be into the page.
- For Wire 2 (I2 = 40A) at the position of Wire 3:
- The distance is also d/2.
- The direction of the magnetic field due to Wire 2 at the position of Wire 3 will be out of the page.
- Let’s denote the distance between Wire 1 and Wire 2 as d. The magnetic field at the position of Wire 3 due to Wire 1 (B1) and Wire 2 (B2) can be calculated as:
B1=μ0⋅202π⋅d2=40μ02πd
B2=μ0⋅402π⋅d2=80μ02πd
- Since B1 is into the page and B2 is out of the page, the net magnetic field (B_net) at Wire 3 will be:
Bnet=B2−B1=80μ02πd−40μ02πd=40μ02πd
- The net magnetic field is directed out of the page.
- The magnetic force (F) on a current-carrying wire in a magnetic field is given by:
F=I⋅L⋅B⋅sin(θ)
- Here, I = 20A (current in Wire 3), L is the length of Wire 3, and θ = 90° (since the current is perpendicular to the magnetic field).
- Therefore, the force on Wire 3 (F3) is:
F3=20A⋅L⋅40μ02πd
- The direction of the force, using Fleming's Left-Hand Rule, will be towards Wire 2 (the 40A wire).
- The net magnetic force on the wire carrying 20A (Wire 3) will be directed towards the wire carrying 40A.
The magnetic force on the wire carrying 20A will be directed towards the wire carrying 40A.
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - exercise
60 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - worked out examples
15 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
Similar Questions
Two parallel wires are carrying electric currents of equal magnitude and in the same direction. They
View SolutionTwo long parallel copper wires carry current of 5A each in opposite directions. If the wires are separated by a distance distance of 0.5m, then the force per unit length between the two wires is
View Solution
Knowledge Check
Two parallel wires 2 m apart carry currents of 2 A and 5 A respectively in same direction, the force per unit length acting between these two wires is
A2×10−6Nm−1B3×10−6Nm−1C1×10−6Nm−1D4×10−6Nm−1The two linear parallel conductors carrying currents in the opposite direction…………………each other.
AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is the correct explanation of assertion.CIf assertion is true but reason is falseDIf both assertion and reason are false.
Two parallel wires separated by a distance of 10cm carry currents of 10 A and 40 A along the same direction, Where should a third current be placed so that it experience no magnetic force?
View SolutionTwo parallel long wires carry currents 18A and 3A. When the currents are in the same direction, the magnetic field at a point midway between the wire is B1. If the direction of i2 is reversed, the field becomes B2. Then the value of B1/B2 is
View SolutionThree long straight and parallel wires carrying currents are arranged as shown in the figure. The wire C which carreis a current of 5.0amp is so placed that it experiences no force. The distance of wire C from D is then
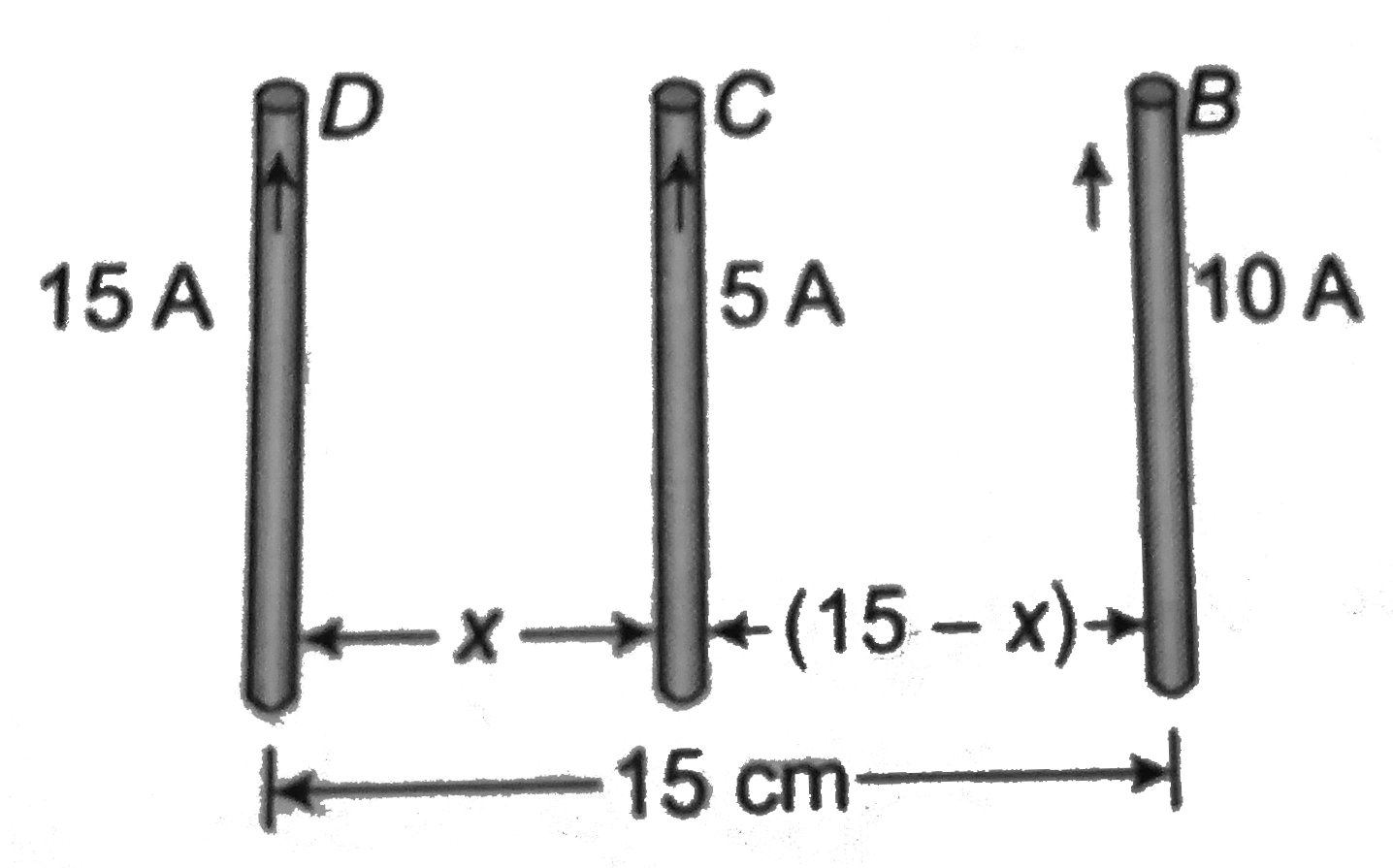
View SolutionThree long straight and parallel wires carrying currents are arranged as shown in the figure. The wire C which carreis a current of 5.0amp is so placed that it experiences no force. The distance of wire C from D is then

View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View SolutionIn fig. two long parallel wires carry equal currents in opposite directions. Point O is situated midway between the wires and X−Y plane contains the two wires and the position Z-axis comes normally out of the plane of paper. The magnetic field B at O is non-zero along
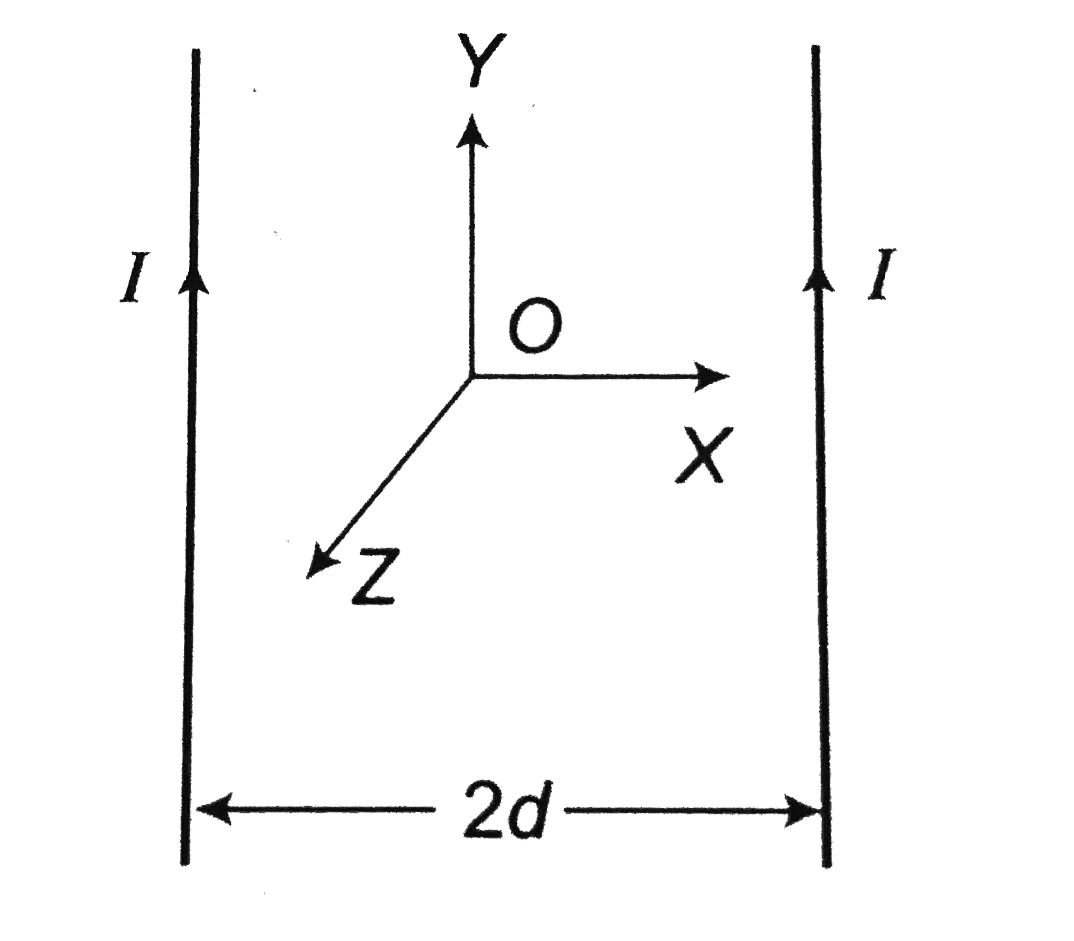
View Solution