Consider a long, straight wire of cross-sectional area A carrying a current i. Let there be n free electrons per unit volume. An observed places himself on a trolley moving in the direction opposite to the current with a moving in the direction opposite to the current with a speed (v= i/nAe) and separated from the wire by a distance r. The magnetic field seen by the observer is very nearly
μ0i2πr
zero
μ0iπr
(2μ0)iπr
The correct Answer is:A
To solve the problem, we need to analyze the situation involving a long straight wire carrying a current and an observer moving in the opposite direction to the current. The magnetic field produced by the wire at a certain distance can be calculated using Ampère's law.
1. Identify the Parameters:
- Current in the wire, I
- Cross-sectional area of the wire, A
- Number of free electrons per unit volume, n
- Distance from the wire to the observer, r
- Speed of the observer, v=InAe
2. Determine the Magnetic Field Due to the Wire:
The magnetic field B at a distance r from a long straight wire carrying a current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
3. Analyze the Observer's Motion:
The observer is moving with a speed v in the direction opposite to the current. Given that v=InAe, we can compare this speed to the drift velocity of the electrons in the wire.
4. Compare Speeds:
The speed of the current is typically very high (close to the speed of light, c≈3×108 m/s). The drift velocity of electrons, on the other hand, is much smaller. Since the observer's speed v is derived from the drift velocity, it is much smaller than the speed of current.
5. Conclusion on Magnetic Field Perception:
Since the speed of the observer is negligible compared to the speed of the current, the magnetic field experienced by the observer will not change significantly due to their motion. Therefore, the magnetic field they perceive is approximately the same as that calculated from the wire's current.
6. Final Expression for the Magnetic Field:
Thus, the magnetic field seen by the observer is:
B≈μ0I2πr
Answer:
The magnetic field seen by the observer is very nearly:
B=μ0I2πr
- Current in the wire, I
- Cross-sectional area of the wire, A
- Number of free electrons per unit volume, n
- Distance from the wire to the observer, r
- Speed of the observer, v=InAe
The magnetic field B at a distance r from a long straight wire carrying a current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
The observer is moving with a speed v in the direction opposite to the current. Given that v=InAe, we can compare this speed to the drift velocity of the electrons in the wire.
The speed of the current is typically very high (close to the speed of light, c≈3×108 m/s). The drift velocity of electrons, on the other hand, is much smaller. Since the observer's speed v is derived from the drift velocity, it is much smaller than the speed of current.
Since the speed of the observer is negligible compared to the speed of the current, the magnetic field experienced by the observer will not change significantly due to their motion. Therefore, the magnetic field they perceive is approximately the same as that calculated from the wire's current.
Thus, the magnetic field seen by the observer is:
B≈μ0I2πr
The magnetic field seen by the observer is very nearly:
B=μ0I2πr
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - exercise
60 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - worked out examples
15 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
Similar Questions
A long straight wire of circular cross- section carries a current along its length. On the axis inside the wire, it follows that
View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionA long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
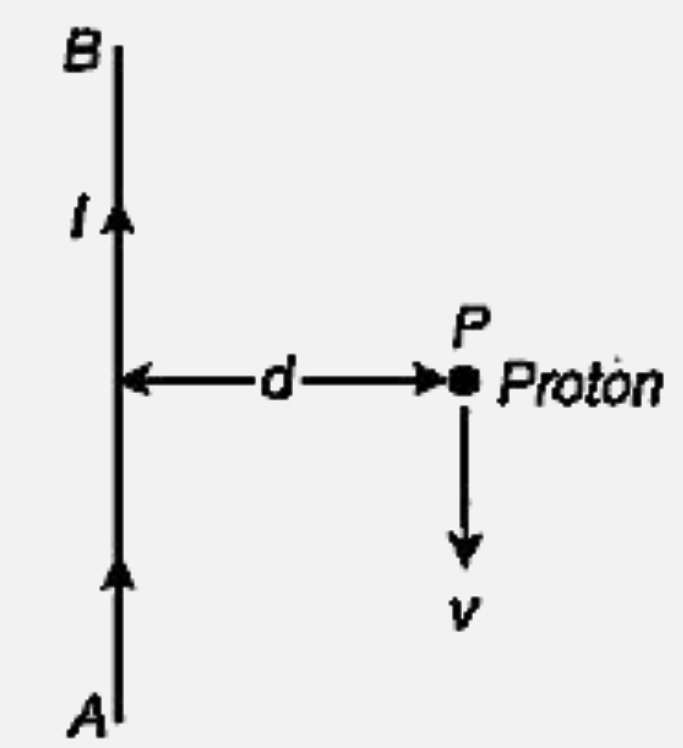
View SolutionA long straight wire AB carries a current I. A proton P travels with a speed v, parallel to the wire at a distance d from it in a direction opposite to the current as shown in the figure. What is the force experienced by the proton and what is its direction?
View SolutionWhen a current is established in a wire, the free electrons drift in the direction opposite to the current, Does the number of free electrons in the wire continuously decrease?
View SolutionA long straight wire of a circular cross section (radius a) carrying steady current. Current is uniformly distributed in the wire. Calculate magnetic field inside the region (r<a) in the wire.
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View SolutionA circular loop of radius r carries a current i. How should a long, straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the center becomes zero?
View SolutionA circular loop of radius r carries a current i. where should a long , straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
View Solution
