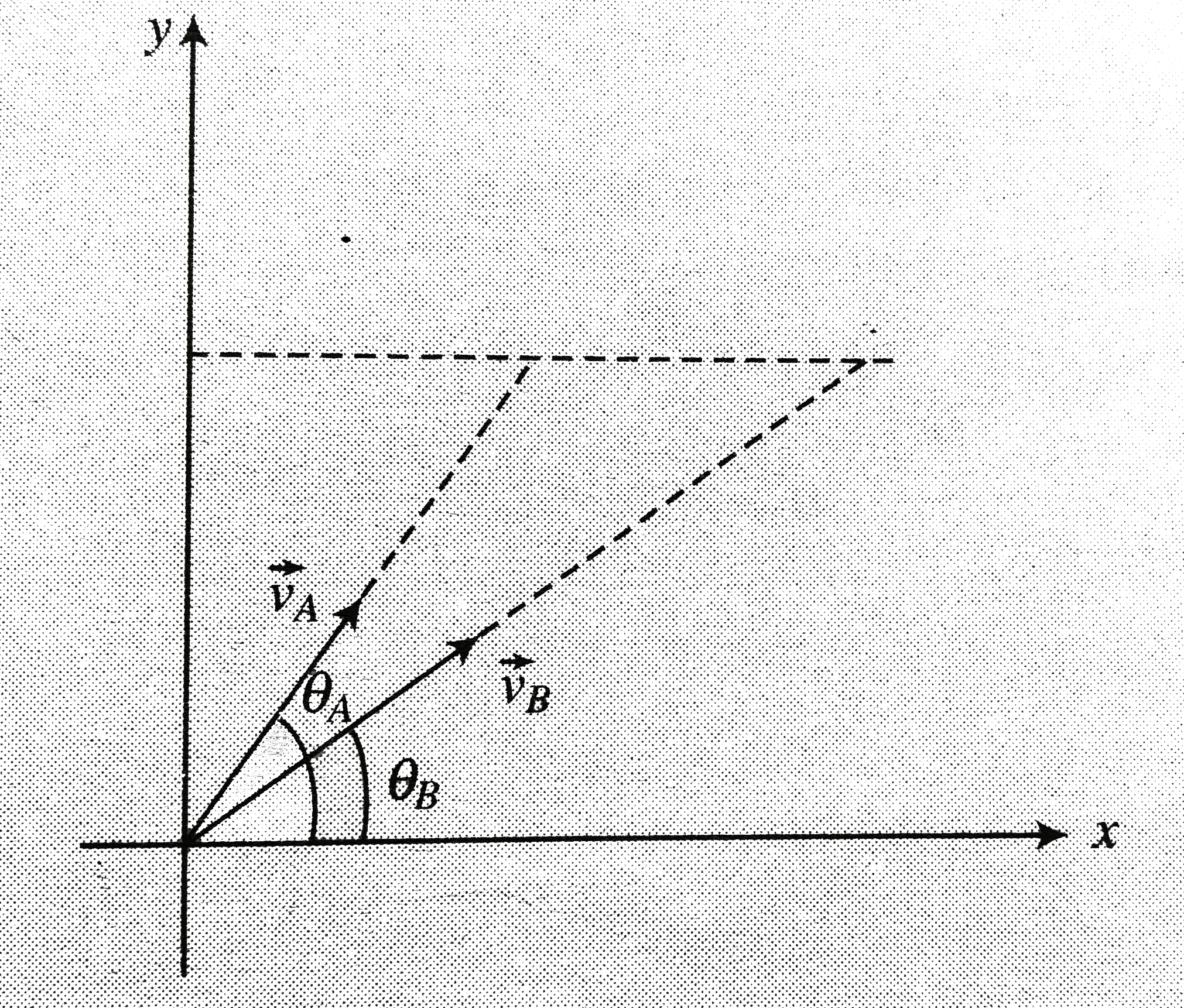
Two particles AandB are projected from the same point in different directions in such a manner that vertical components of their initial velocities are same (Fig. 5.8). Find the ratio of range.
 .
.
Range of the projectile , in terms of velocity components can be written as followings:
R=2uxuyg
Let u1andu2 be the initial speed of projection for P and Q respectively .
Rp2(u1cosα)(u1sinα)g
RQ=2(u2cosβ)(u2sinβ)g
It given that u1sinα=u2sinβ, hence we can divide the above relations to get the following :
RpRQ=u1u2×cosαcosβ
Future we can substitute u1u2=sinβsinα
⇒RpRQ=sinβsinα×xosαcosβ
⇒RpRQ=tanβtanα
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - NCERT FILE (Solved) NCERT (Textbook Exercises)
25 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - NCERT FILE (Solved) (NCERT (Additional Exercises))
7 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Conceptual Questions
23 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
Similar Questions
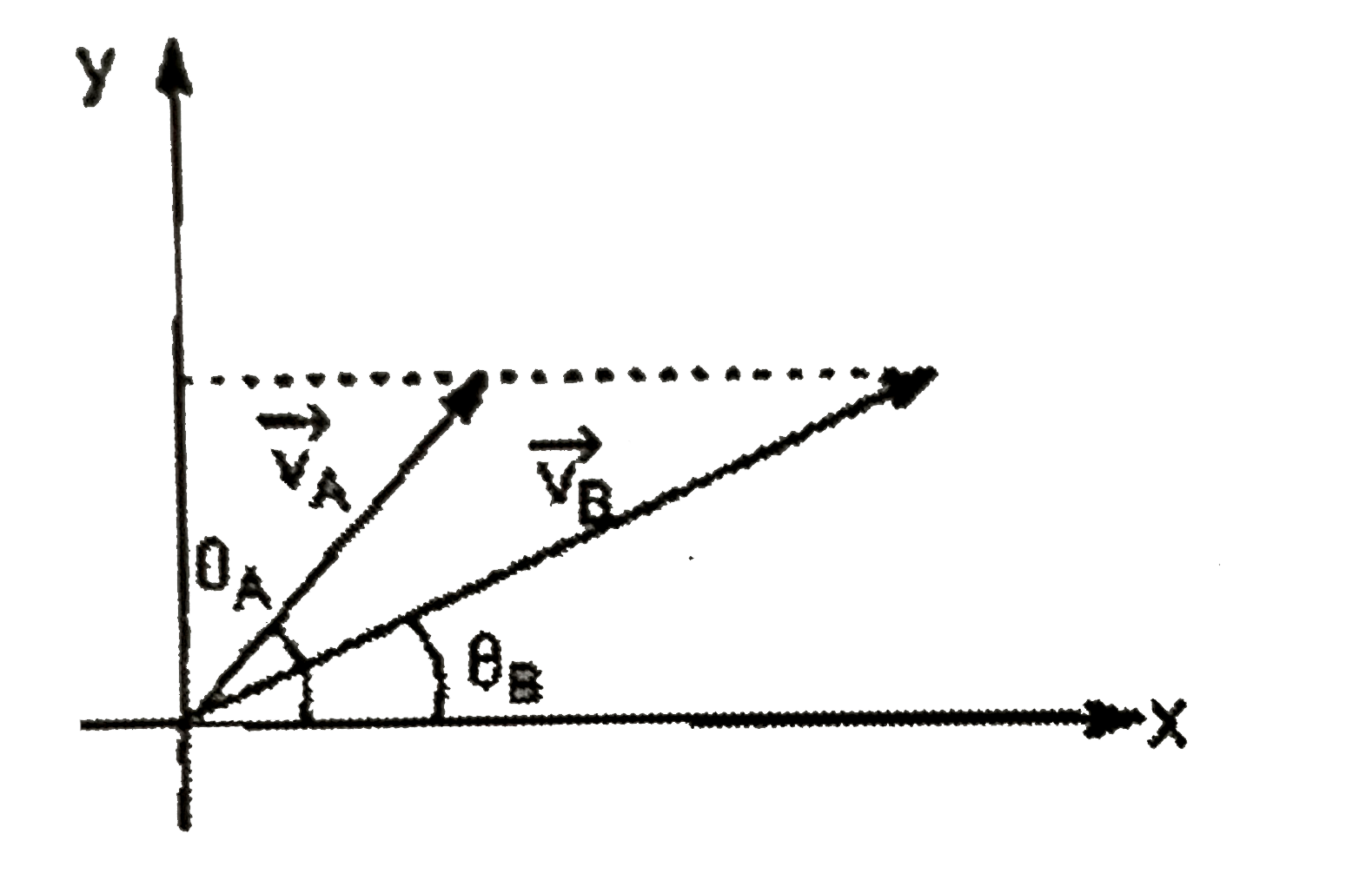
Iwo particles A & B are projected from the same point in, different directions in such a manner that vertical components of their initial velocities are same :
(a) Find ratio of time of flight
(b) Find ratio of range.
View SolutionTwo bodies are projected from the same point with same velocity but in different directions. If the range in each case be Rand the times of flight be t and t' then R=... in terms of t,t'
View Solution
Knowledge Check
Two particles A and B are projected from the same point in different direction in such a manner that their velocity vectors are shown in the diagram :−
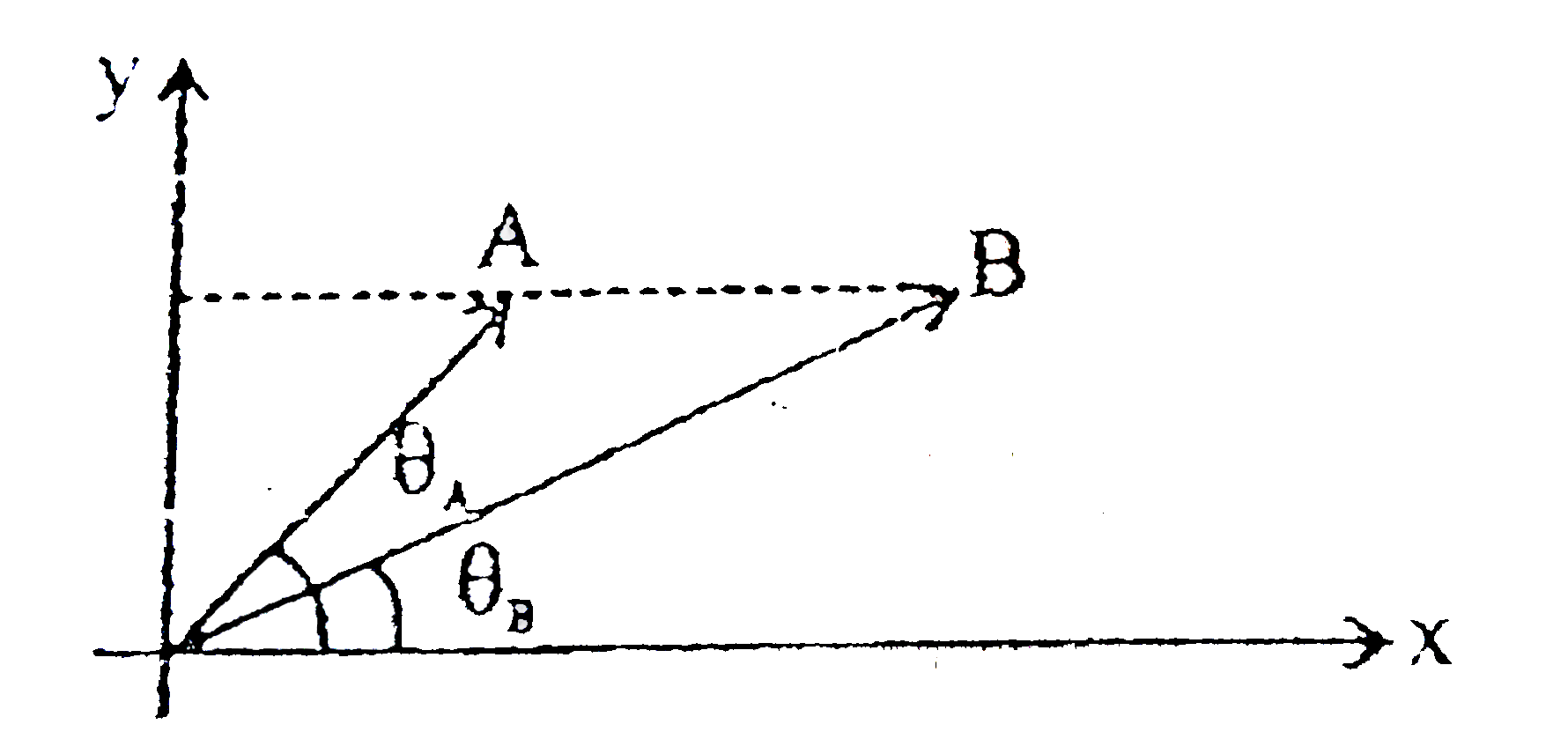 .ATA=TBBTA>TBCTA<TBDCan't be determined
.ATA=TBBTA>TBCTA<TBDCan't be determinedA number of particles are projected from a given point with equal velocities in different directions in the same vertical plane. At any instant they will lie on
AparabolaBcircleChyperbolaDrectangleTwo projectiles thrown from the same point at angles 60∘and30∘ with the horizontal attain the same height. The ratio of their initial velocities is
A1B2C√3D1√3
Two particles P and Q are projected from two points in the same plane as shown. Find the condition for collision of two paricles.
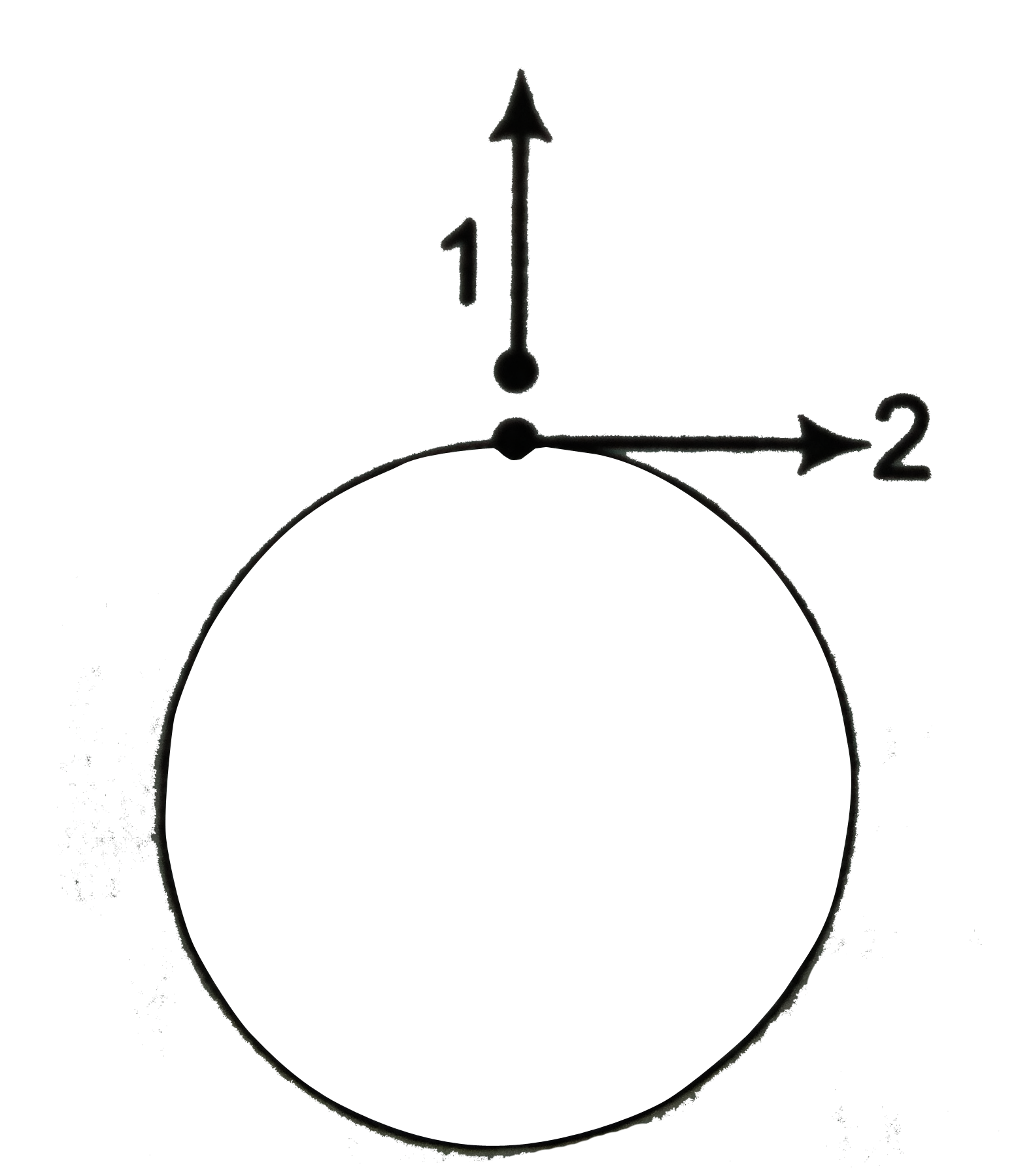
View SolutionTwo identical particles 1 and 2 are projected from surface of earth with same velocities in the directions shows in figure.
View SolutionTwo particles A and B are projected from the same point with the same velocity of projection but at different angles αand β of projection, such that the maximum height of A is two-third of the horizontal range of B. then which of the following relations are true?
View SolutionTwo particles A and B are projected from the same point with the same velocity of projection but at different angles αand β of projection, such that the maximum height of A is two-third of the horizontal range of B. then which of the following relations are true?
View SolutionTwo particle A and B projected along different directions from the same point P on the ground with the same velocity of 70 m/s in the same vertical plane. They hit the ground at the same point Q such that PQ = 480,. Then [g=9.8m/s2]
View Solution
