Two particles A and B each of mass m are kept stationary by applying a horizontal force F=mg on particle B as show in figure .Then
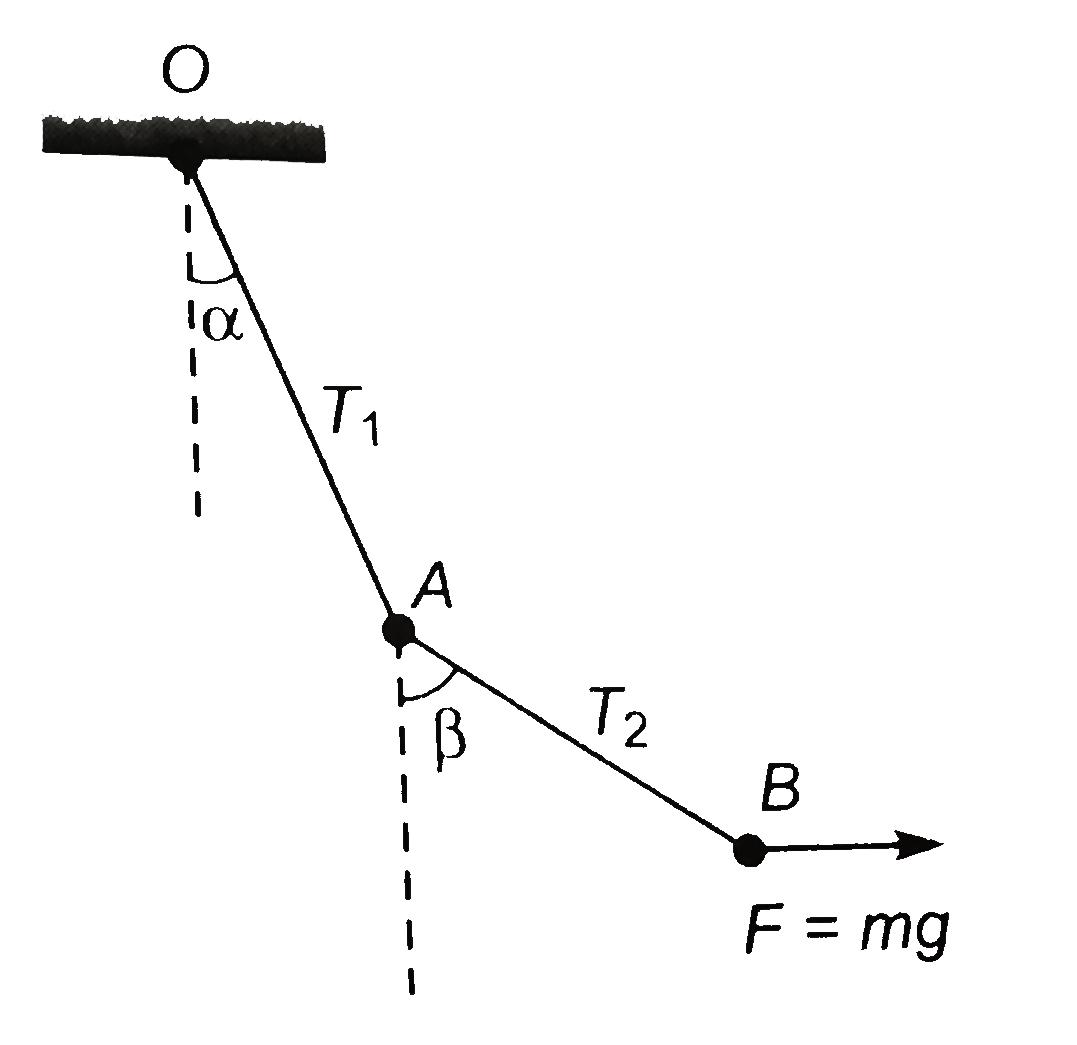
2tanβ=tanα
2T1=5T2
T1√2=T2√5
None of these
The correct Answer is:C
From fig, T2cosθ=mg,T2sinθ=mg
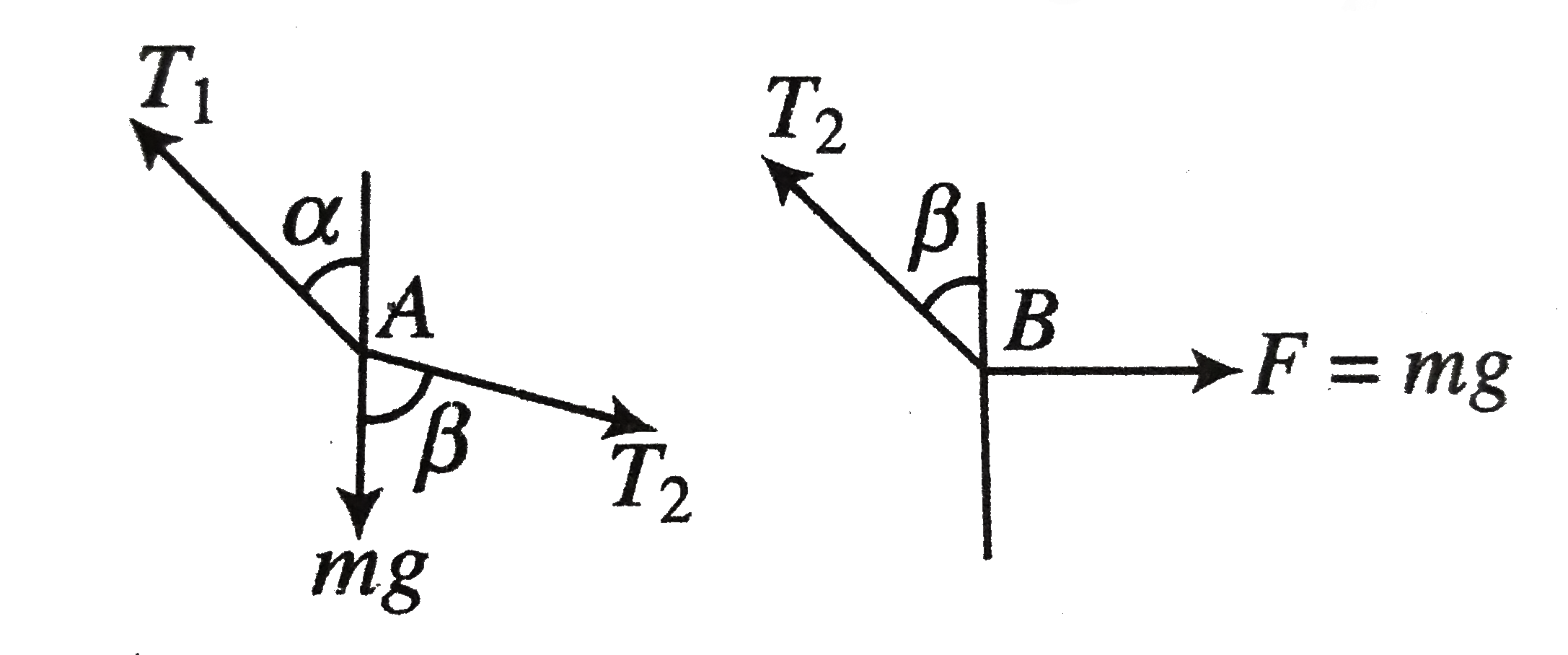
T1sinα=mg√2sin45∘
T1sinα=mg⇒cosαsinα=2mgmg
tanα=12⇒cosα=2√5
T12√5=2mg⇒T1=mg√5
T1T2=√5√2⇒√2T1=√5T2.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning
15 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective
15 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
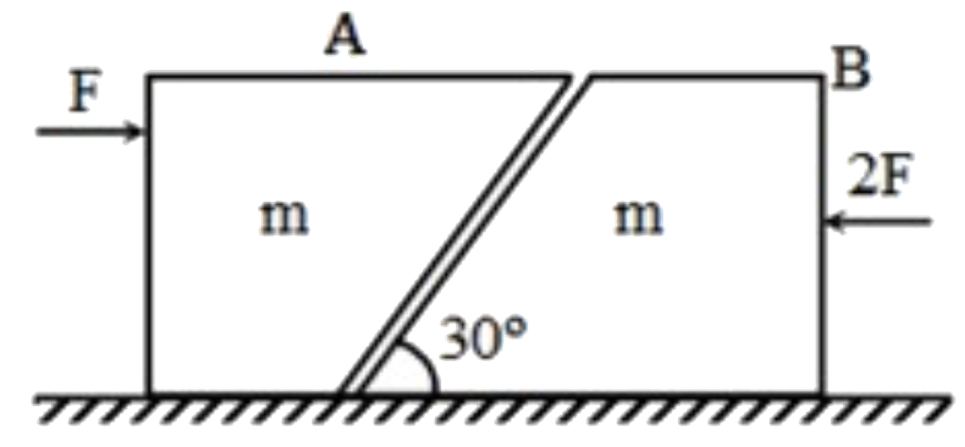
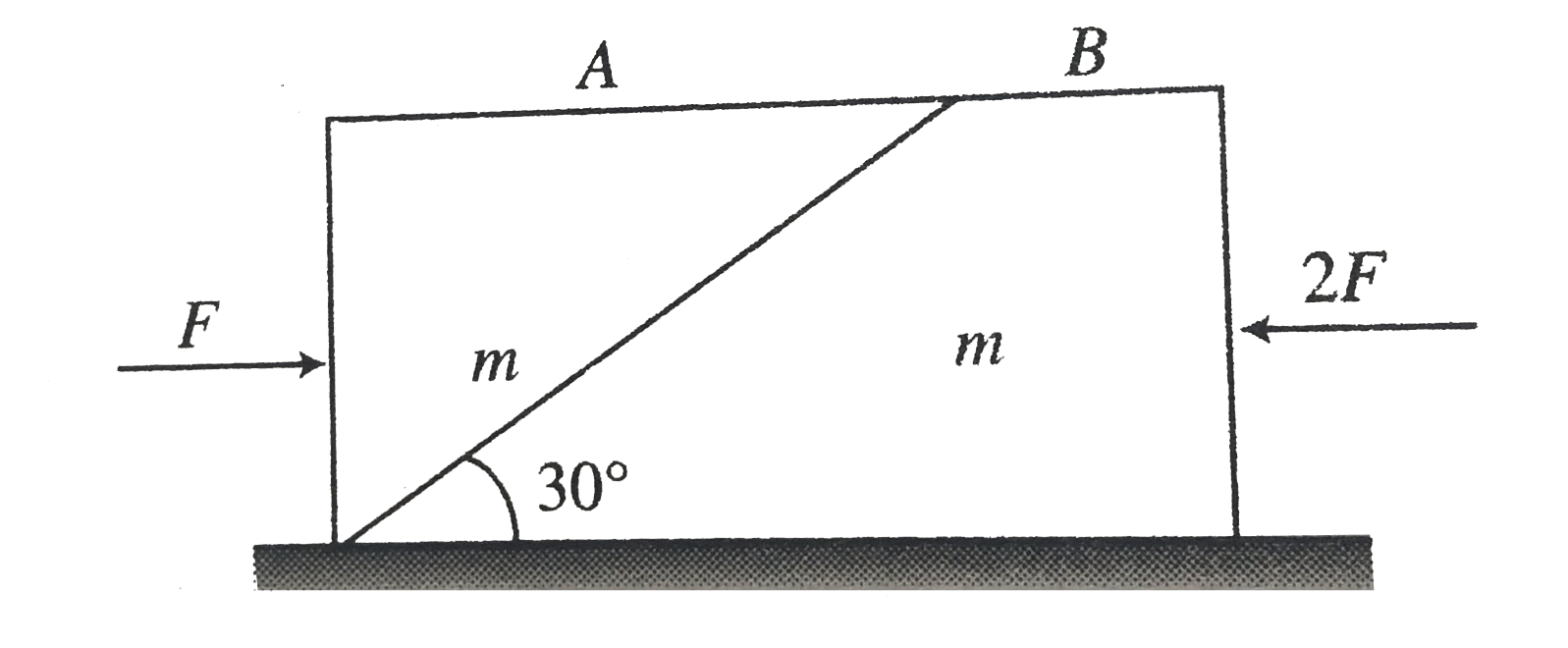
Two blocks 'A' and 'B' each of mass 'm' are placed on a smooth horizontal surface . Two horizontal force F and 2F are applied on the blocks A and B , respectively , as shown in figure . The block A does not slide on block B . The normal reaction acting between the two blocks is
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
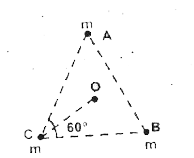
Force acting on particle C, due to particle A and B
View Solution
Knowledge Check
Two particalA and B each of mass m are kept stationary by applying a horizontal force F=mg on partical B as show in figure .Then
 Atanβ=2tanαB2T1=5T2C√2T1=√5T2Dα=β
Atanβ=2tanαB2T1=5T2C√2T1=√5T2Dα=βTwo particles A and B each of mass m are kept stationary by applying a horizontal force F=mg on particle B as show in figure .Then
 A2tanβ=tanαB2T1=5T2CT1√2=T2√5DNone of these
A2tanβ=tanαB2T1=5T2CT1√2=T2√5DNone of theseTwo particle A & B each of mass m are in equilibrium in a vertical plane under action of a horizontal force F=mg on particle B, as shown in figure Then :
 A2T1=5T2BT1√2=T2√5Ctanθ=2tanαDNone of these
A2T1=5T2BT1√2=T2√5Ctanθ=2tanαDNone of these
Four particles A,B, C and D each of mass m are kept at the corners of a square of side L. Now the particle D is taken to infinity by an external agent keeping the other particles fixed at their respective positions . The work done by the gravitational force acting on the particle D During its movement is
View SolutionTwo identicle particles A and B, each of mass m, are interconnected by a spring of stiffness k. If particle B experiences a forec F and the elongation of the spring is x, the acceleration of particle B relative to particle A is equal to

View SolutionTwo small particles P and Q each of mass m are fixed along x-axis at points (a,0) and (-a,0). A third particle R is kept at origin. Then
View SolutionTwo blocks A and B each of mass m are placed on a smooth horizontal surface. Two horizontal force F and 2F are applied on blocks A and B, respectively, as shown in fig. Block A does not slide on block B. Then then the normal reaction acting between the two blocks is (assume no friction between the blocks)
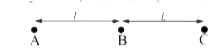
View SolutionThree particles A, B and C of mass m, m and 2m lie in a straight line as shown. The only force acting on these particles is due to the gravitational attraction towards each other. Let the magnitude of net force on them be FA,FB and FC respectively. Then,FA:FB:FC is equal to :
View Solution
