Two small rings O and O' are put on two vertical stationary rods AB and A'B', respectively. One end of an inextensible thread is tied at point A'. The thread passes through ring O' and its other end is tied to ring O. Assuming that ring O' moves downwards at a constant velocity v1, then velocity v2 of the ring O, when ∠AOO'=α is
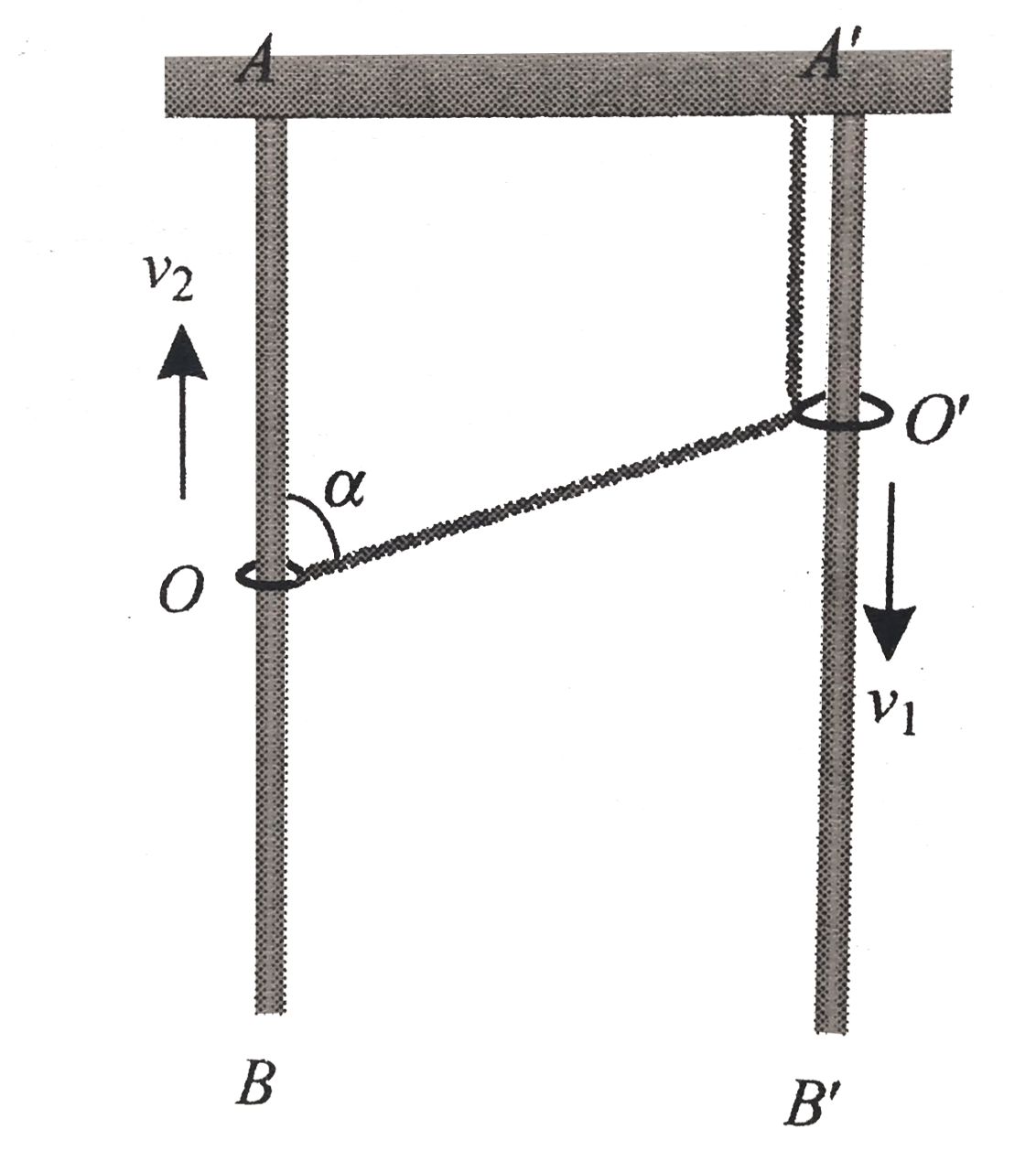
v1[2sin2α/2cosα]
v1[2sin2α/2sinα]
v1[3sin2α/2sinα]
None of these
The correct Answer is:A
v2cosα+v1cosα=v1⇒v2=v1[2sin2(α/2)cosα].
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning15videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective15videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
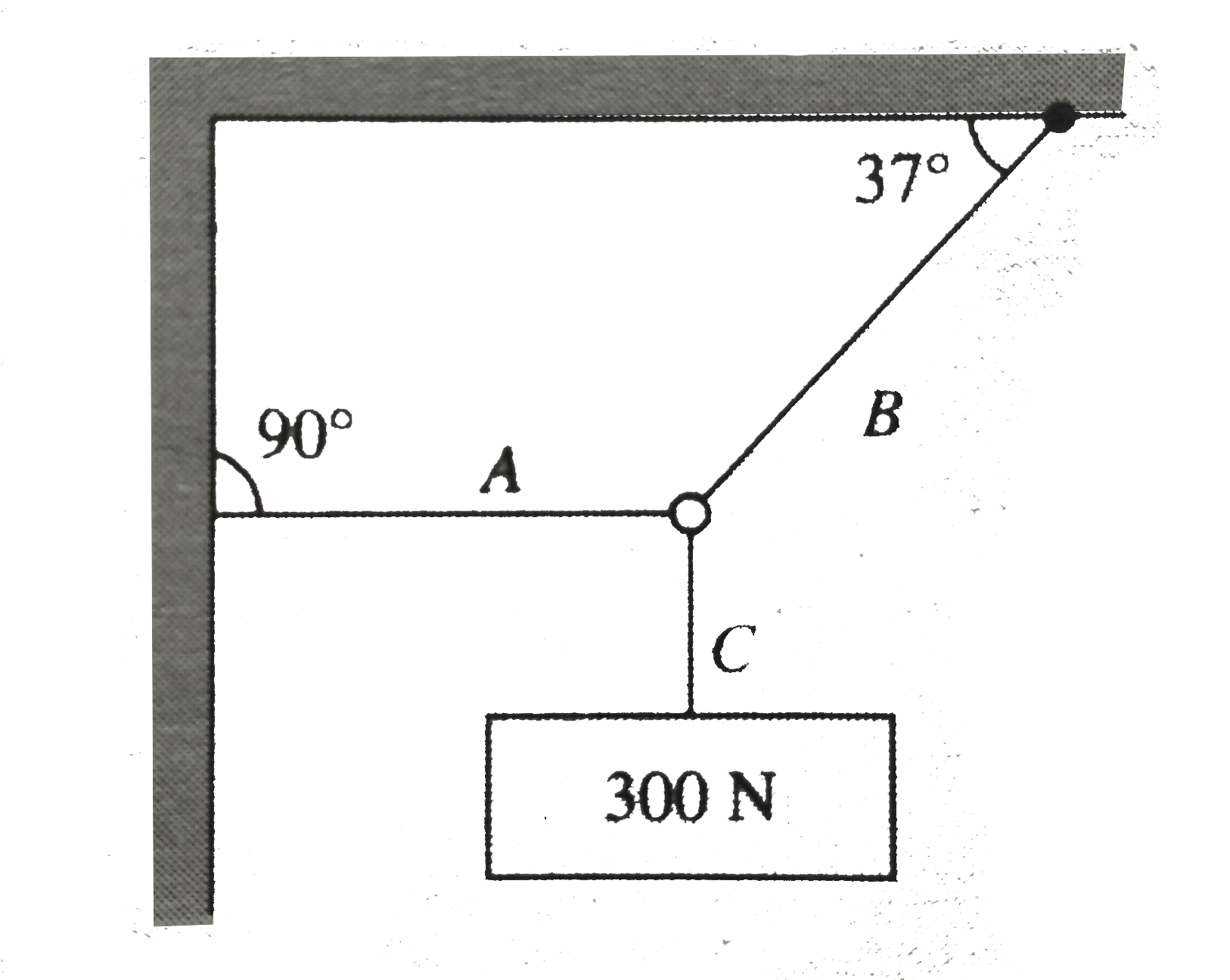
A block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.
 06:06View Solution
06:06View SolutionStatement I: The driver of a moving car sees a wall in front of him. To avoid collision, he should apply brakes rather than taking a turn away from the wall.
Statement II: Frictional force is needed to stop the car or taking a turn on a horizontal road.02:44View SolutionA hot- air balloon consists of a basket, one passenger, and some carge. Let the total mass be M. Even though there is an upward lift force on the balloon, the balloon is initially acceleration downwards at a rate of g/3.
(a) Draw a free-body diagram for the descending balloon.
(b) Find the upward lift force in terms of the initial total weight Mg.
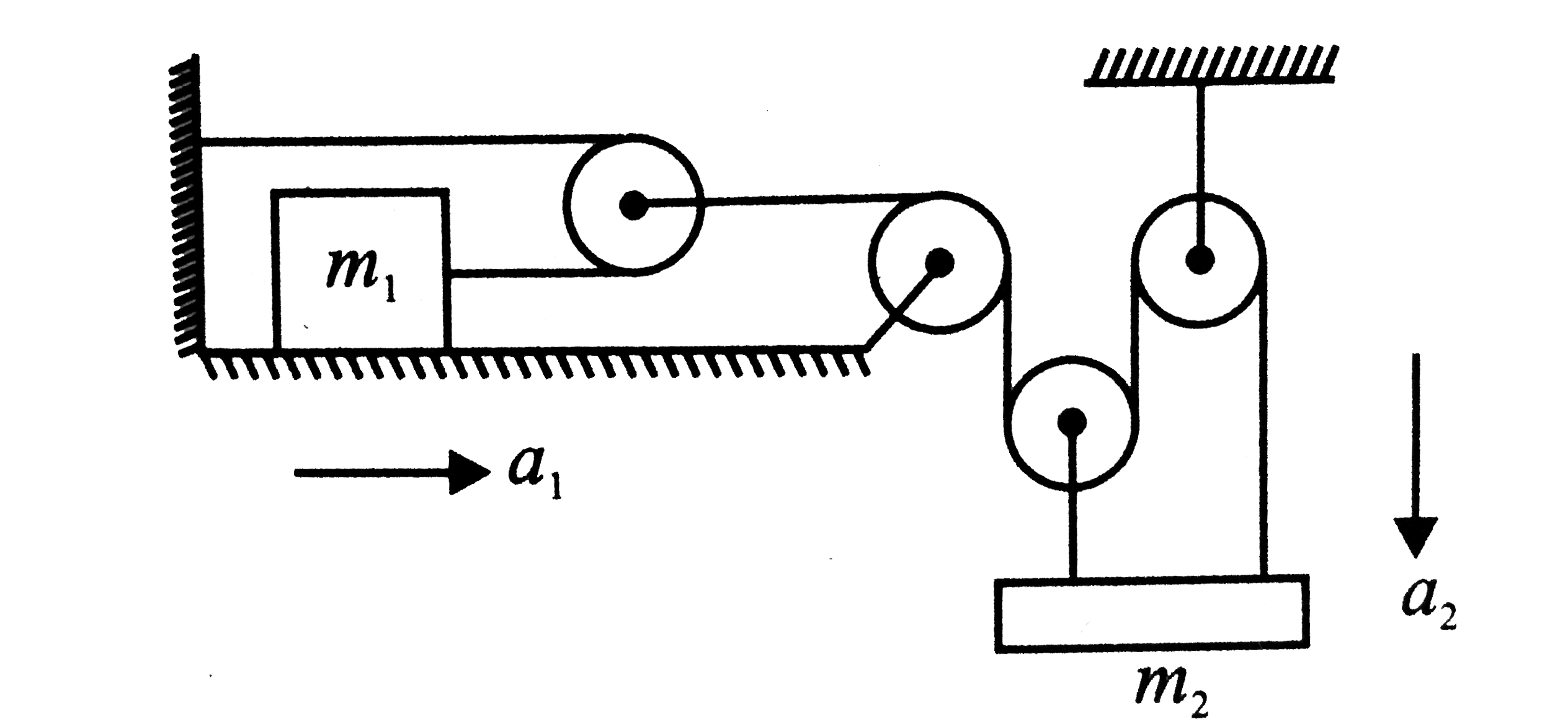
(c ) The passenger notices that he is heading straight for a waterfall and decides he needs to go up. What fraction of the total weight must he drop overboard so that the balloon accelerates upward at a rate of g/2? Assume that the upward lift force remains the same.04:21View SolutionTwo blocks are arranged as shown in figure. Find the ratio of a1/a2. (a1 is acceleration of m1 and a2 that of m2)
 03:06View Solution
03:06View SolutionA block is moving on an inclined plane making an angle 45∘ with the horizontal and the coefficient of friction is μ. The force required to just push it up the inclined plane is 3 times the force required to just prevent it from sliding down. If we define N=10μ, then N is
01:17View SolutionAn impulse J is applied on a ring of mass m along a line passing through its centre O . The ring is placed on a rough horizontal surface. The linear velocity of centre of ring once it starts rolling without slipping is
04:49View SolutionA disk is fixed at its centre O and rotating with constant angular velocity omega . There is a rod whose one end is connected at A on the disc and the other end is connected with a ring which can freely moce along the fixed vertical smooth rod. At an instant when the rod is making an angle 30^(@) with the vertical the ring is found to have a velocity v in the upward direction. Find omega of the disk. Given that the point A is R//2 distance above point O and length of the rod Ab is l
03:38View SolutionTwo rings O and O' are put on two vertical stationary rods AB and A'B' respectively as shown in figure. An inextensible string is fixed at point A' and on ring O and is passed through O' moves downwards at a constant speed v, find the velocity of the ring O in terms of alpha .
04:50View SolutionA copper ring is suspended in a vertical plane by a thread. A stell bar is passed through the ring in a horizontal direction and then a magnet is passed through it moving along the axis of ring. Will the motion of the bar and the magnet affect the position of the ring?
 06:45View Solution
06:45View SolutionA portion of a ring of radius R has been removed as shown in figure. Mass of the remaining portion is m. Centre of the ring is at origin O. Let IAandIO be the moment of inertia passing through points A and O are perpendicular to the plane of the ring. Then,
 06:32View Solution
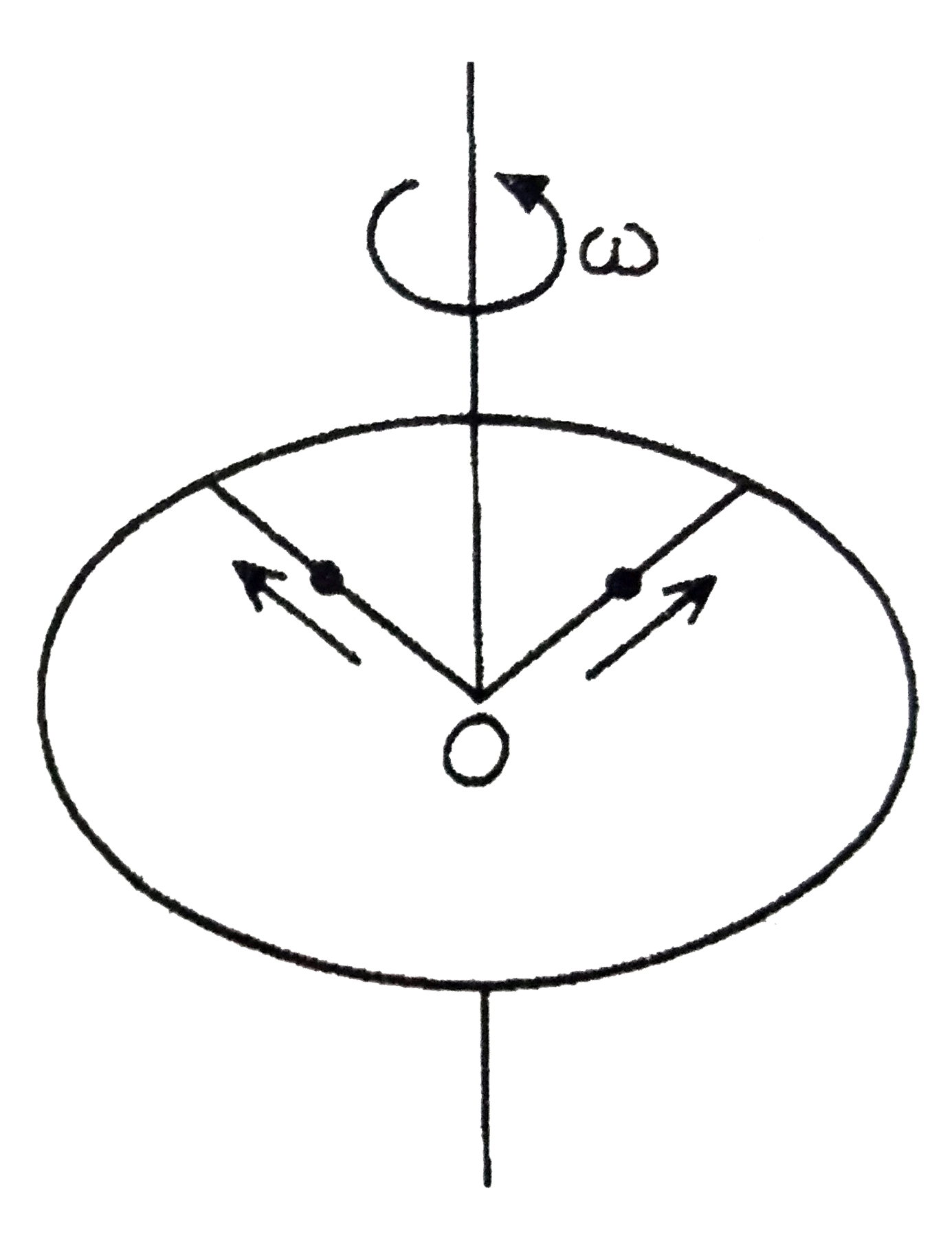
06:32View Solutionद्रव्यमान M तथा त्रिज्या R का एक छल्ला अपने केंद्र से होकर जाने वाली स्थिर ऊर्ध्वाधर अक्ष के परितः कोणीय वेग ω से घूम रहा है। इस क्षण M/8 द्रव्यमान के दो बिंदु द्रव्यमान छल्ले के केंद्र O पर विराम स्थिति में है। वो दर्शाये चित्रानुसार छल्ले पर लगी द्रव्यमानहीन दो छड़ों पर त्रिज्यतः बाहर की ओर गति कर सकतेक हैं किसी क्षण पर निकाय की कोणीय गति 89ω है तथा बिंदु द्रव्यमान O से 35R दूरी पर है। इस क्षण दूसरे बिंदु द्रव्यमान की O से दूरी होगी:
 View Solution
View SolutionA thin circular ring of radius r is uniformly charged over its length.Consider two points,the centre of ring 0 ,and a point P on the axis of the ring at a distance a from the centre of the ring.If ratio of potential at points O and P is V0Vp=√101, then value of ar is ..
06:22View SolutionRing is fixed on the horizontal surface and a rod starts rotatiing with constant angular velocity omega fixed at O as shown in the figure. Find the magnitude of velocity of intersection points of rod and ring when aplha become 90^(@)
05:05View Solutionएक छल्ला जिसका द्रव्यमान M तथा त्रिज्या R है केंद्र O से होकर जाने वाले स्थिर उध्र्वाधर अक्ष के चारों ओर (i) कोणीय गति से घूम रहा है । स समय पर M8 द्रव्यमान के दो बिंदु द्रव्यमान छल्ले के केंद्र O पर विराम स्थिति में हैं । वे चित्र में दर्शाए अनुसार छल्ले पर लगी द्रव्यमान रहित दो छड़ों के त्रिजात: बहार की ओर गति कर सकते हैं । किसी एक क्षण पर निकाय की कोणीय गति 89ω तथा एक द्रव्यमान O से 35 की दूरी पर है । इस क्षण दूसरे बिंदु द्रव्यमान की O से दूरी होती -
 04:19View Solution
04:19View SolutionA rigid horizontal smooth rod AB of mass 0.75 kg and length 40 cm can rotate freely about a fixed vertical axis through its mid-point O. Two rings each of mass 1 kg initially at rest at a distance 10 cm from O on either side of the rod. The rod is rotated with angular velocity of 30 rad s^(-1) . When the rings reach the ends of the rod, the angular velocity of the rod is :
04:07View SolutionA smooth rod of length l rotates freely in a horizontal plane with the angular velocity about a stationary vertical axis O as shown in Fig. The moment of inertia of the rod is equal to I relative to the axis. A small ring of mass m is located on the rod close to the rotation axis and is tied to it by a thread. When the thread is burned, the ring starts sliding radially outwards along the rod. Find the velocity v of the ring relative to the rod as a function of its distance r from the rotation axis.
02:35View Solution

