Two particles A and B of masses m and 2m have charges q and 2q respectively. Both these particle moving with velocities v1andv2 respectively in the same direction enter the same magnetic field B acting normally to their direction of motion. If the two force FAandFB acting on them are in the ratio 1:2 , find the ratio of their velocities.
As force F=qvB, hence FAFB=12=qAvABqBvBB=qvA2qvB=vA2vB⇒vA=vB
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - SHORT ANSWER QUESTIONS
41 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - LONG ANSWER QUESTIONS-I
33 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - ASSERTION-REASON TYPE QUESTIONS
5 Videos
- MODEL TEST PAPER 3 (UNSOLVED)BOOK - U-LIKE SERIESCHAPTER - MODEL TEST PAPER 3 (UNSOLVED)EXERCISE - SECTION A
3 Videos
- NUCLEIBOOK - U-LIKE SERIESCHAPTER - NUCLEIEXERCISE - Self Assessment Test
10 Videos
Similar Questions
Two particles of masses m and 2m moving in opposite directions collide elastically with velocity 2v and v, respectiely. Find their velocities after collision.

View SolutionTwo particles of masses m and 2m moving in opposite directions collide elastically with velocity 2v and v, respectiely. Find their velocities after collision.

View Solution
Knowledge Check
A proton and an alpha-particle enter a magnetic field in a direction perpendicular to it. If the force acting on the proton is twice that acting on the alpha-particle , the ratio of their velocities is
A4:1B1:4C1:2D2:1Two particles A and B of masses 10 kg and 38 kg, respectively, are moving along the same straight line with velocities 15 m/s and 3 m/s, respectively, in the same direction. After elastic collision, the velocities of A and B are vAand vB, respectively, in the direction of initial motion. Then
 AvA=20m/s,vB=8msBvA=–4m/s,vB=8m/sCvA=16ms,vB=28m/sDvA=–5m/s,vB=10m/s
AvA=20m/s,vB=8msBvA=–4m/s,vB=8m/sCvA=16ms,vB=28m/sDvA=–5m/s,vB=10m/sTwo particles AandB of masses mAandmB respectively and having the same charge are moving in a plane . The speeds of the particles are vAandvB respectively and the trajectories are as shown in the figure. Then
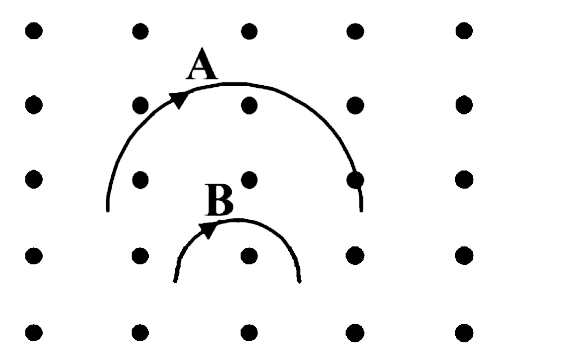 AmAvA<mBvBBmAvA>mBvBCmAvA<mBandvA<vBDmA=mBandva=vB
AmAvA<mBvBBmAvA>mBvBCmAvA<mBandvA<vBDmA=mBandva=vB
Two balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare: The force needed to stop them in the same
View SolutionTwo objects having same mass 'm' are moving with velocities v and 2v. Find ratio of their kinetic energies.
View SolutionTwo particles having identical masses and charges 2Q and Q are moving with velocities v and 2v resp. In uniform magnetic field B. Find ratio of radius of circle described by them
View SolutionA particle of mass M at rest decays into two particles of masses m1andm2 having velocities V1andV2 respectively. Find the ratio of de- Broglie wavelengths of the two particles
View SolutionTwo charged particles of charge +2q and +q have masses m and 2m respectively. Then are kept in uniform electric field allowed to move for the same time. Find the ratio of their kinetic energies.
View Solution
