Two particles are simultaneously thrown in horizontal direction from two points on a riverbank, which are at certain height above the water surface. The initial velocities of the particles are v1=5m/sandv2=7.5m/s respectively. Both particles fall into the water at the same time. First particles enters the water at a point s = 10 m from the bank. Determine
(a) the time of flight of the two particles,
(b) the height from which they are thrown,
(c) the point where the second particle falls in water.
The correct Answer is:A, B, C
To solve the problem step by step, we will analyze the motion of both particles thrown horizontally from the same height.
Step 1: Determine the time of flight of the two particles
Both particles are thrown simultaneously and fall into the water at the same time. The time of flight can be determined using the horizontal motion of the first particle.
Given:
- Horizontal distance traveled by the first particle, s1=10m
- Initial velocity of the first particle, v1=5m/s
Using the formula for horizontal motion:
s=v⋅t
We can rearrange this to find the time t:
t=s1v1=10m5m/s=2s
Step 2: Determine the height from which they are thrown
Now that we have the time of flight, we can calculate the height H from which both particles are thrown. The vertical motion can be described by the equation:
H=12gt2
where g is the acceleration due to gravity (approximately 10m/s2).
Substituting the values:
H=12⋅10m/s2⋅(2s)2=12⋅10⋅4=20m
Step 3: Determine the point where the second particle falls in water
For the second particle, we need to calculate the horizontal distance it travels before hitting the water. The initial velocity of the second particle is v2=7.5m/s. Using the same time of flight t=2s:
s2=v2⋅t=7.5m/s⋅2s=15m
Summary of Results
(a) Time of flight of the two particles: t=2s
(b) Height from which they are thrown: H=20m
(c) The point where the second particle falls in water: s2=15m
---
- Horizontal distance traveled by the first particle, s1=10m
- Initial velocity of the first particle, v1=5m/s
s=v⋅t
We can rearrange this to find the time t:
t=s1v1=10m5m/s=2s
H=12gt2
where g is the acceleration due to gravity (approximately 10m/s2).
H=12⋅10m/s2⋅(2s)2=12⋅10⋅4=20m
s2=v2⋅t=7.5m/s⋅2s=15m
(a) Time of flight of the two particles: t=2s
(b) Height from which they are thrown: H=20m
(c) The point where the second particle falls in water: s2=15m
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Single Correct
10 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 More Than One Correct
8 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 1 Single Correct
16 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
The uncertainties in the potisition and velocity of particle are 3.14×10−10m and5.27×10−24m/s respectively . Calculate mass of the particle.
View SolutionTwo particles are simultaneously thrown from the top of two towards as shown. Their velocities are 2ms−1and14ms−1. Horizontal and vertical separations between these particles are 22 m and 9 m respectively. Then the minimum separation between the particles in the process of their motion in meters is (g=10ms−2)
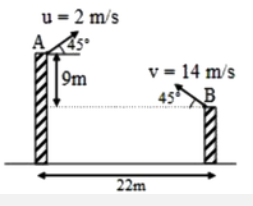
View SolutionA particle is projected up with initial speed u=10ms−1 from the top of a bitlding at time t=0. At time t=5s the particle strikes the fround. Find the height of the building.
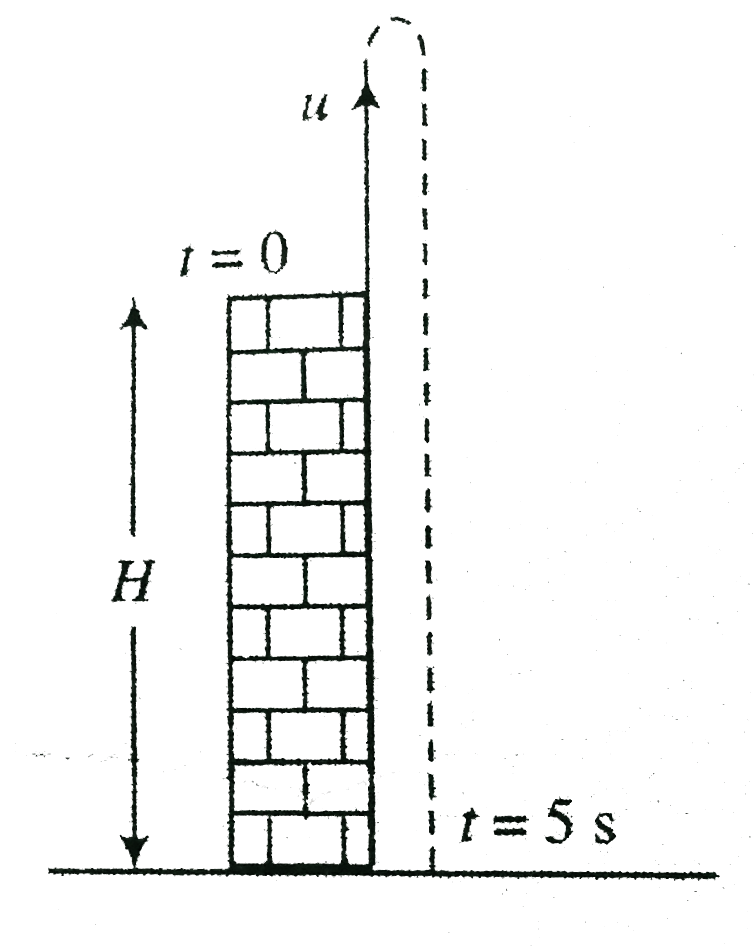 .
.
View SolutionThe components of a particles velocity in the directions at right angles are 3m/s,4m/sand 12m/s respectively . The actual velocity of the particle , in m/s is
View SolutionA particle (A) is dropped from a height and another particles (B) is thrown into horizontal direction with speed of 5m/s sec from the same height. The correct statement is
View SolutionThe velocity of a particle in S.H.M. at positions x1 and x2 are v1 and v2 respectively. Determine value of time period and amplitude.
View SolutionA body is moving with constant acceleration, a=5ms2 from A to B in straight line AB. The velocity of particle at A and B are 5 m/s and 15 m/s respectively. The velocity at mid-point of AB is
View SolutionVelocity of a particle is given as v=(2t2−3)m/s. The acceleration of particle at t = 3s will be :
View SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA particle is thrown with velocity u at an angle ∝ from the horizontal. Another particle is thrown with the same velocity at an angle ∝ from the verticle. What will be the ratio of times of flight of two particles ?
View Solution
