Two particles each of mass m and speed v, travel in opposite direction along parallel lines separated by a distance d. Show that the vector angular momentum of this system of particles is the same about any point taken as origin.
To solve the problem, we need to calculate the angular momentum of two particles of mass m moving with speed v in opposite directions along parallel lines separated by a distance d. We will show that the vector angular momentum of this system is the same about any point taken as the origin.
1. Identify the System:
- We have two particles, each of mass m.
- One particle moves in the positive direction along one line, and the other moves in the negative direction along a parallel line.
2. Define the Geometry:
- Let’s denote the distance between the two parallel lines as d.
- Let’s take a point O (the origin) at a perpendicular distance r1 from the line of the first particle and r2 from the line of the second particle.
3. Angular Momentum of Each Particle:
- The angular momentum \( L \) of a particle about a point is given by the formula:
\(
L = r \times p
\)
where \( r \) is the position vector from the point to the line of motion, and \( p \) is the linear momentum of the particle.
- For the first particle moving with speed \( v \):
\(
L_1 = m v r_1
\)
- For the second particle moving with speed \( -v \) (since it is moving in the opposite direction):
\(
L_2 = m (-v) r_2 = -m v r_2
\)
4. Total Angular Momentum:
- The total angular momentum \( L_{total} \) of the system is the sum of the angular momenta of both particles:
\(
L_{total} = L_1 + L_2 = m v r_1 - m v r_2
\)
- This can be simplified to:
\(
L_{total} = m v (r_1 - r_2)
\)
5. Independence from the Origin:
- The crucial observation is that \( r_1 \) and \( r_2 \) are the perpendicular distances from the origin O to the lines of motion of the particles.
- As we move the origin to any other point along the perpendicular bisector of the two lines, the difference \( r_1 - r_2 \) remains constant because the distance between the two lines (which is \( d \)) does not change.
- Therefore, \( L_{total} = m v (r_1 - r_2) \) remains constant regardless of the choice of the origin.
6. Conclusion:
- Since the total angular momentum \( L_{total} \) does not depend on the position of the origin, we conclude that the vector angular momentum of this system of particles is the same about any point taken as origin.
- We have two particles, each of mass m.
- One particle moves in the positive direction along one line, and the other moves in the negative direction along a parallel line.
- Let’s denote the distance between the two parallel lines as d.
- Let’s take a point O (the origin) at a perpendicular distance r1 from the line of the first particle and r2 from the line of the second particle.
- The angular momentum \( L \) of a particle about a point is given by the formula:
\(
L = r \times p
\)
where \( r \) is the position vector from the point to the line of motion, and \( p \) is the linear momentum of the particle.
- For the first particle moving with speed \( v \):
\(
L_1 = m v r_1
\)
- For the second particle moving with speed \( -v \) (since it is moving in the opposite direction):
\(
L_2 = m (-v) r_2 = -m v r_2
\)
- The total angular momentum \( L_{total} \) of the system is the sum of the angular momenta of both particles:
\(
L_{total} = L_1 + L_2 = m v r_1 - m v r_2
\)
- This can be simplified to:
\(
L_{total} = m v (r_1 - r_2)
\)
- The crucial observation is that \( r_1 \) and \( r_2 \) are the perpendicular distances from the origin O to the lines of motion of the particles.
- As we move the origin to any other point along the perpendicular bisector of the two lines, the difference \( r_1 - r_2 \) remains constant because the distance between the two lines (which is \( d \)) does not change.
- Therefore, \( L_{total} = m v (r_1 - r_2) \) remains constant regardless of the choice of the origin.
- Since the total angular momentum \( L_{total} \) does not depend on the position of the origin, we conclude that the vector angular momentum of this system of particles is the same about any point taken as origin.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.6
4 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.7
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.4
11 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
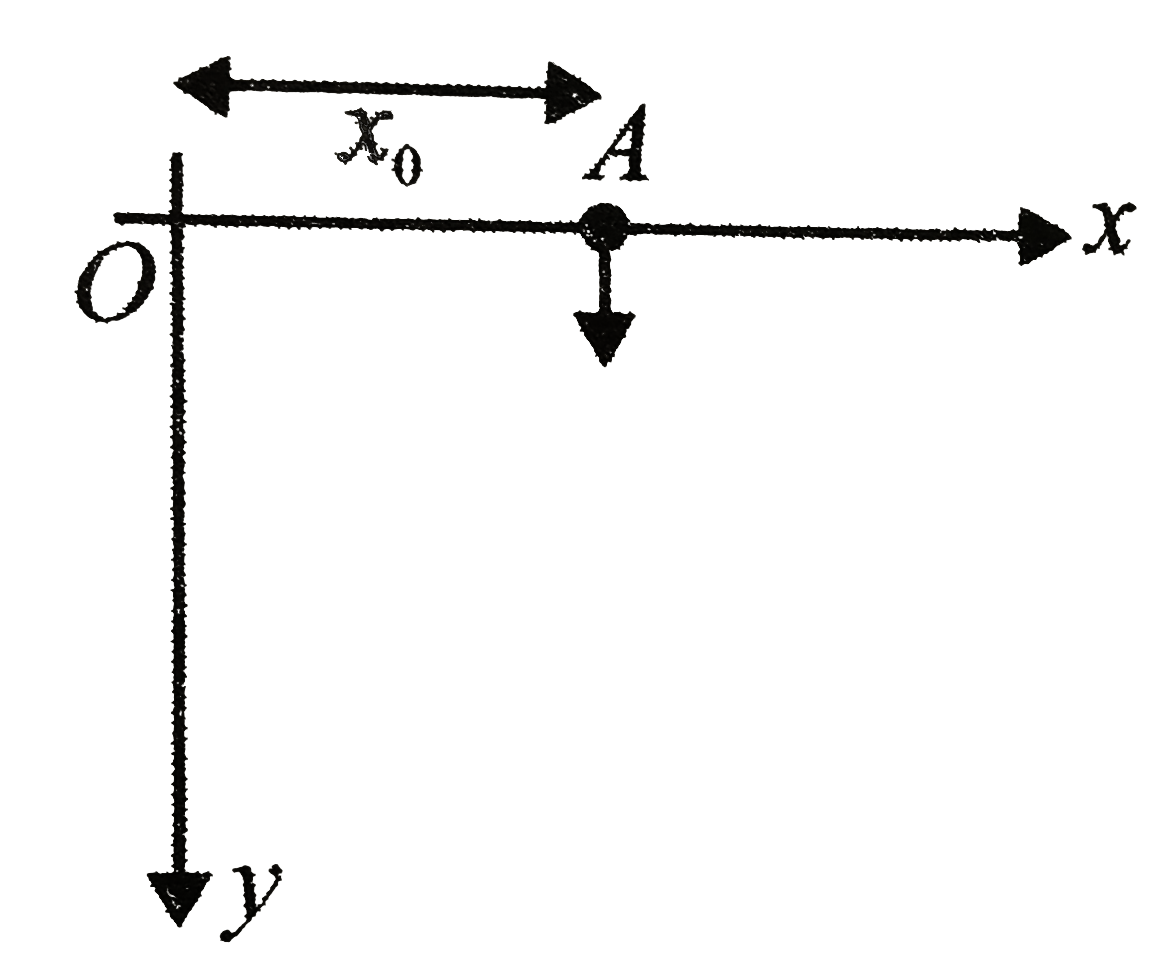
A particle of mass m is released from rest at point A in Fig., falling parallel to the (vertical) y-axis. Find the angular momentum of the particle at any time t with respect to the same origin O.
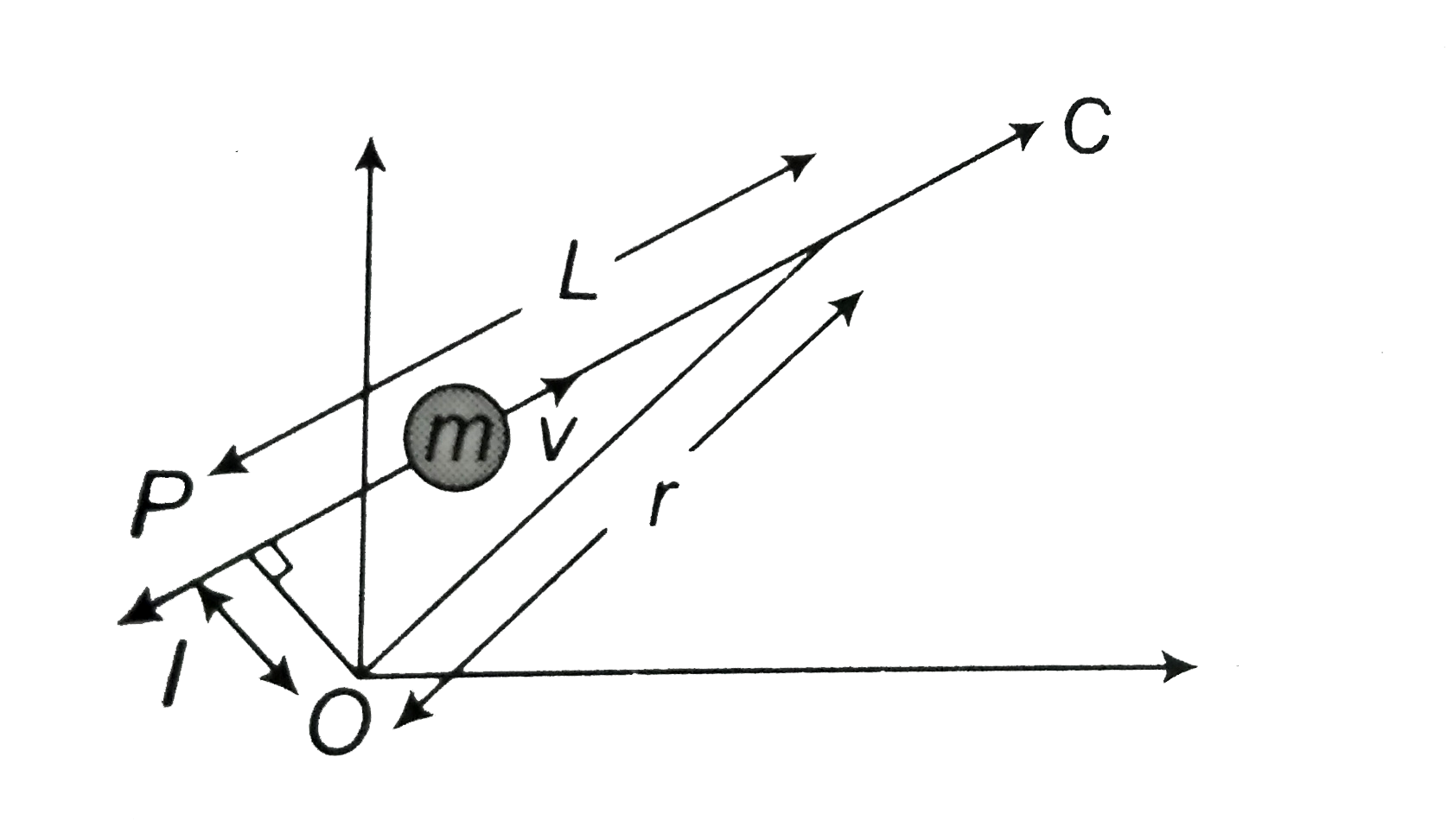
View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?
View Solution
Knowledge Check
Figure shows two identical particles 1 and 2, each of mass m, moving in opposite directions with same speed →V along parallel lines. At a particular instant, →r1 and →r2 are their respective position vectors drawn from point A which is in the plane of the parallel lines. Which of the following is the correct statement ?
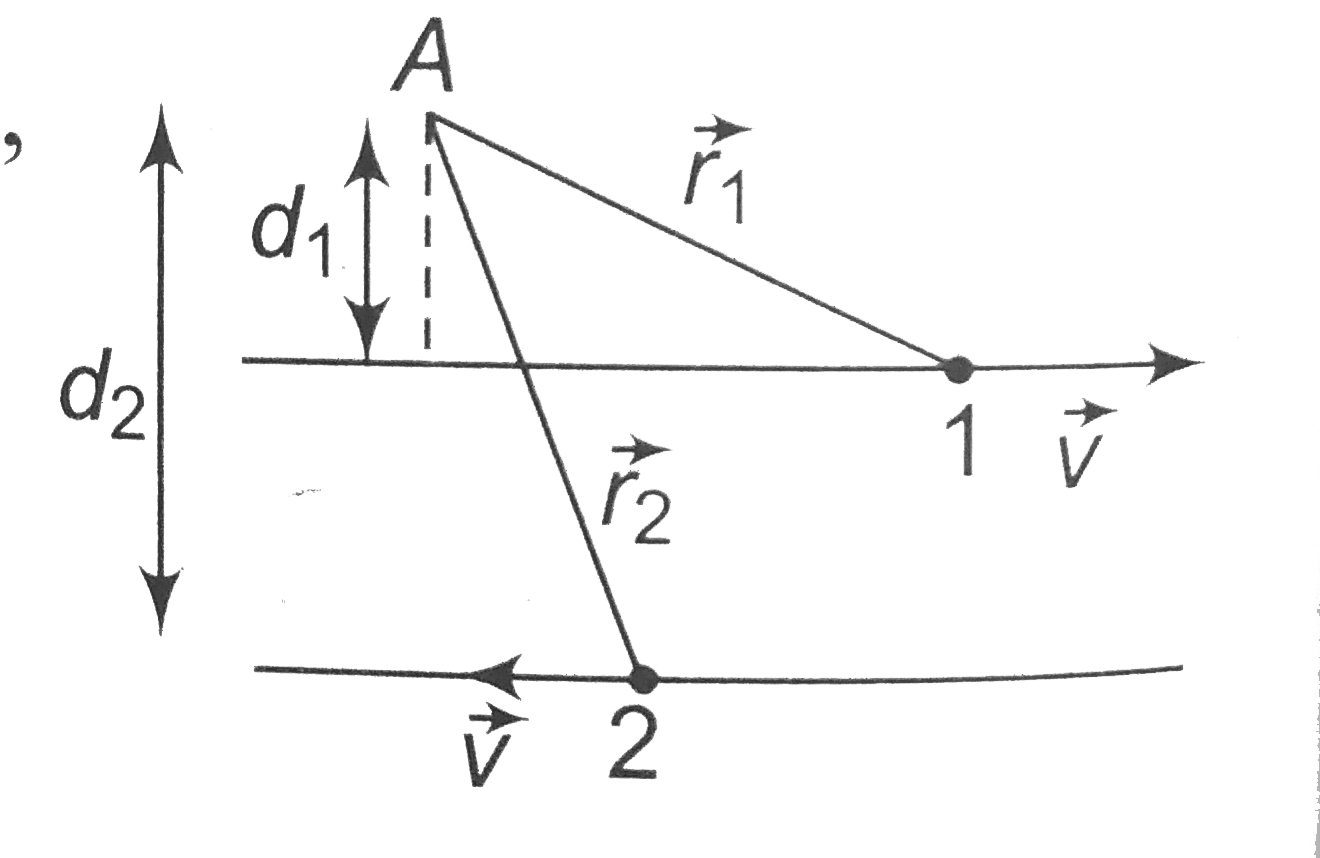 .AAngular momentum →L1 of a particle 1 about A is →L1=mv→r1⊙BAngular momentum →L2 of particle 2 about A is →L2=mv→r2⊙CTotal angular momentum of the system about A is →L=mv(→r1+→r2)⊙DTotal angular momentum of the system about A is →L=mv(d2−d1)⊗
.AAngular momentum →L1 of a particle 1 about A is →L1=mv→r1⊙BAngular momentum →L2 of particle 2 about A is →L2=mv→r2⊙CTotal angular momentum of the system about A is →L=mv(→r1+→r2)⊙DTotal angular momentum of the system about A is →L=mv(d2−d1)⊗
⊗ represents a unit vector going into the page, ⊙ represent a unit vector coming out of the page
Two particles of masses m and 2m moving in opposite directions collide elastically with velocity 2v and v, respectiely. Find their velocities after collision.

View SolutionIf a particle of mass m is thrown with speed at an angle 60° with horizontal, then angular momentum of particle at highest point about point of projection is
View SolutionA particle is moving along a straight line parallel to x-axis with constant velocity. Find angular momentum about the origin in vector form :

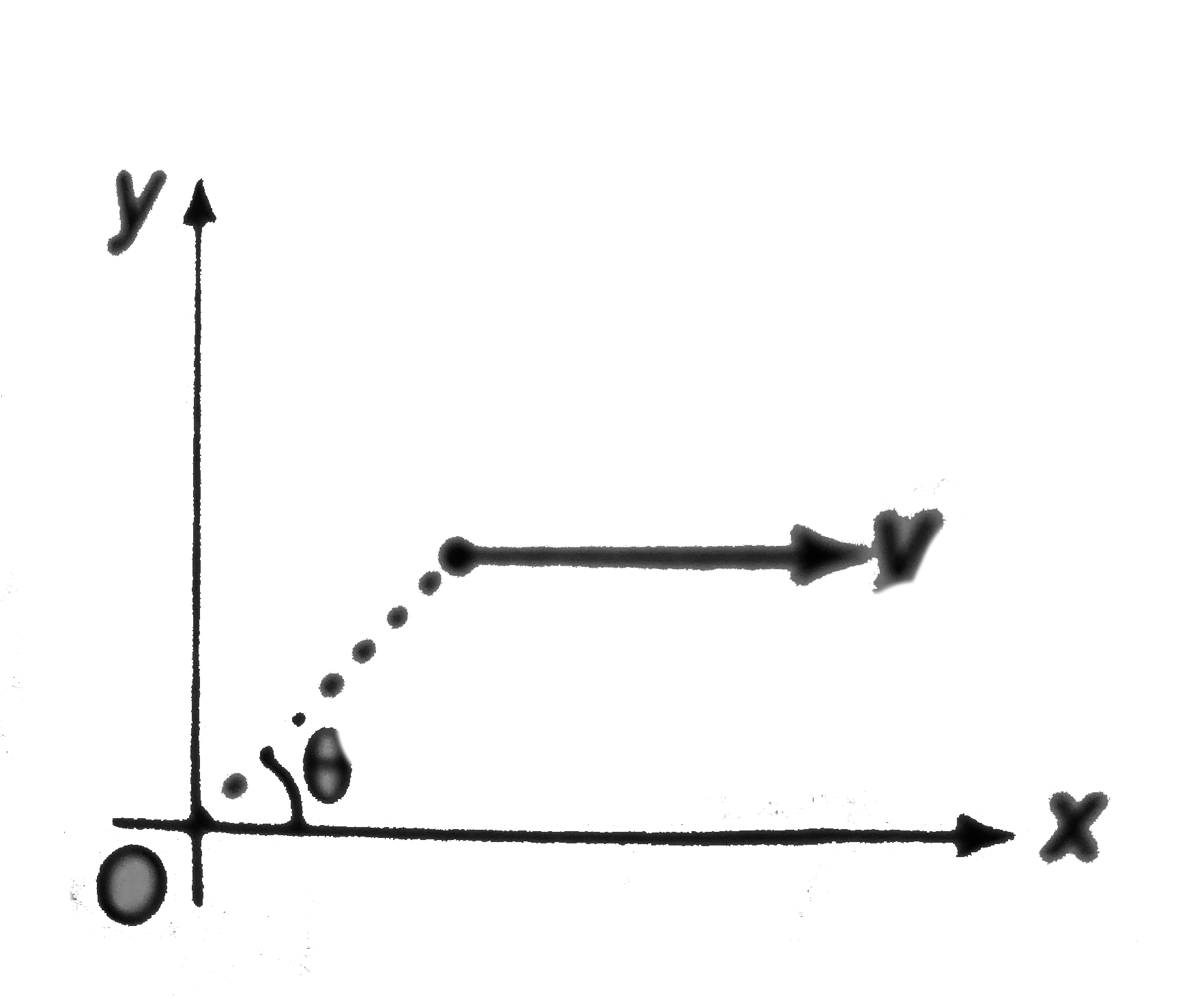
View SolutionA particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin O
View SolutionTwo particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.
View SolutionShow that the angular momentum about any point of a single particle moving with constant velocity remains constant throughout the motion.
View SolutionA particle of mass m moves in the XY plane with constant velocity v along the straight line PQ as shown in the figure. Its angular momentum with respect to origin O is(θ is angle between→v and x-axis)

View Solution
