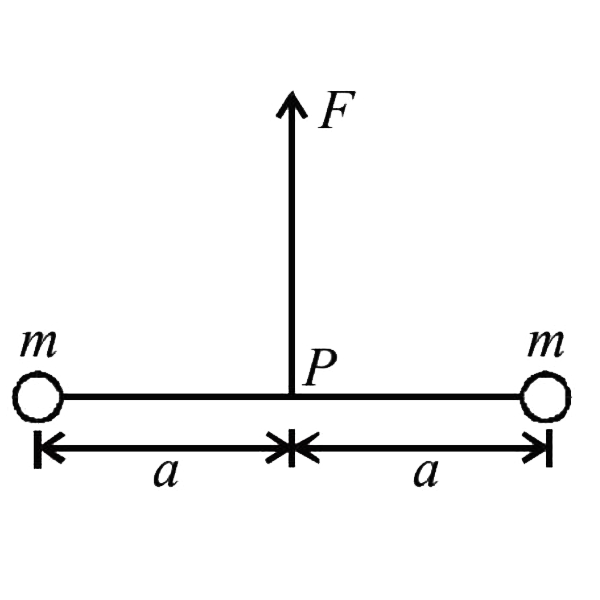
Two particles of mass m each are tied at the ends of a light string of length 2a. The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance a from the centre P (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x, is
F2ma√a2−x2
F2m−x√a2−x2
F2mxa
F2m√a2−x2x
The correct Answer is:B
The arrangement is shown in the figure. The separation between the two masses is 2x. Each mass will move in the horizontal direction as shown in the figure.
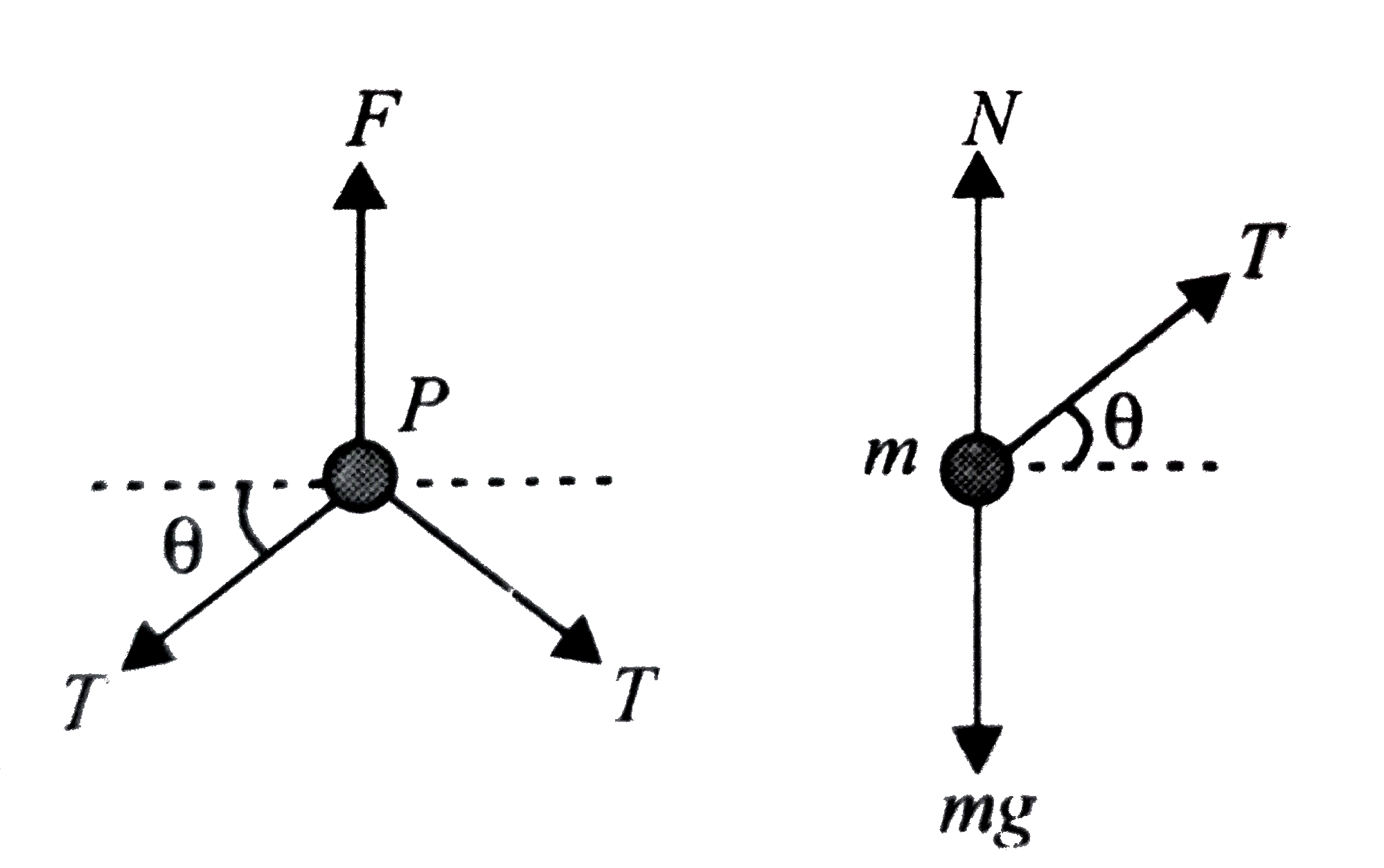
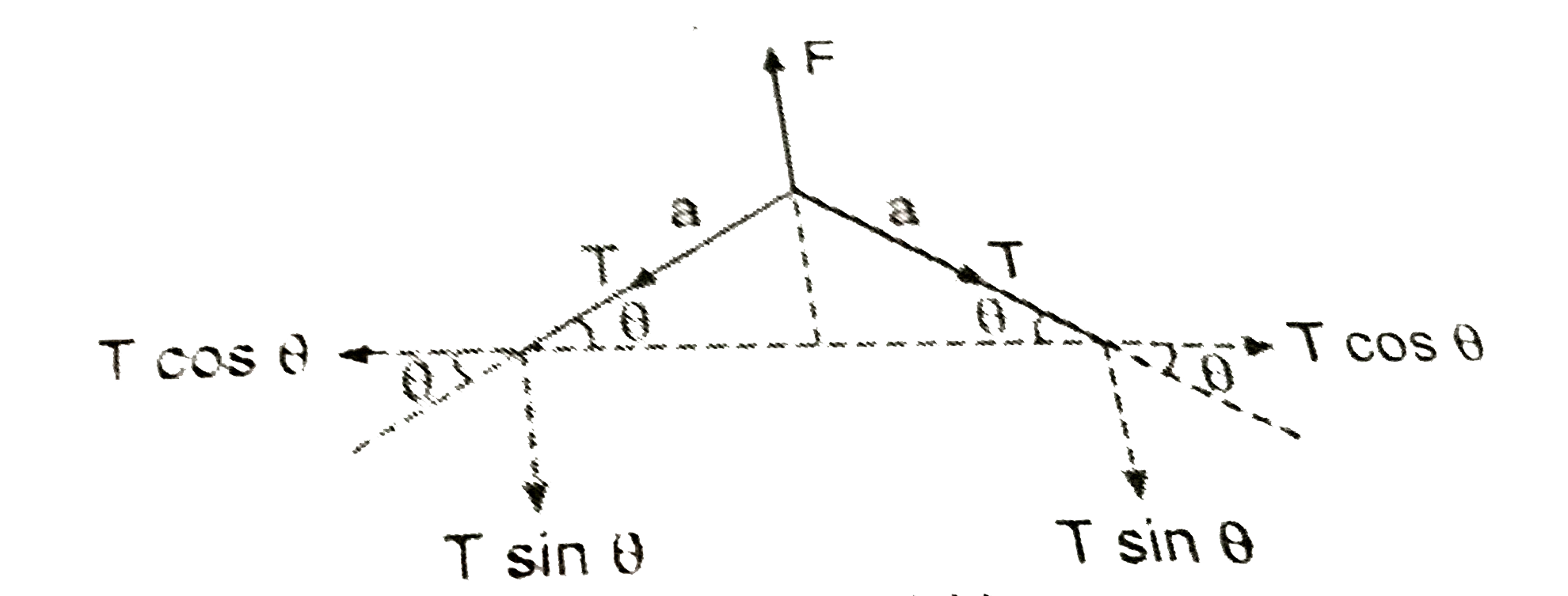
Let the tension in the string be T. The forces acting t point P and on one of the masses are shown in the figure. Net force at point P must equal zero.
∴2Tsin=F...(i)
Also, for the mass m,
N+Tsinθ−mg=0....(ii)
and Tcosθ=mA....(iii)
Equations (i) and (iii) give A=Fcotθ2m=F2m(x√a2−x2)
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - NCERT Exemplar
9 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason
15 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - Solving Problem In Mechanics
16 Videos
- KINETIC THEORYBOOK - NCERT FINGERTIPSCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
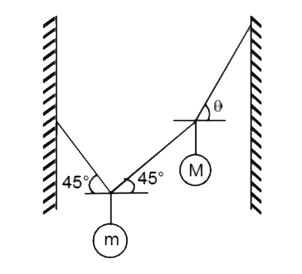
Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibruim, then
View SolutionTwo identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
View Solution
Knowledge Check
Two particles of mass 'm' each are tied at eh ends of a light string of length '2a' The whole system is kept on frictionless horizontal surface with the string held tight so that each mass is at a distance 'a' from the centre P (as shown in figure). Now the mid point of the string is pulled vertically upwards with a small but constant force F As a result, the particles move towards each other on the surface the magnitude of acceleration, when the separation between them becomes 2x is:
 AF2ma√a2−x2BF2mx√a2−x2CF2mxaDF2m√a2−x2x
AF2ma√a2−x2BF2mx√a2−x2CF2mxaDF2m√a2−x2xTwo masses M and m are connected by a weightless string. They are pulled by a force F on a frictionless horizontal surface. The tension in the string will be
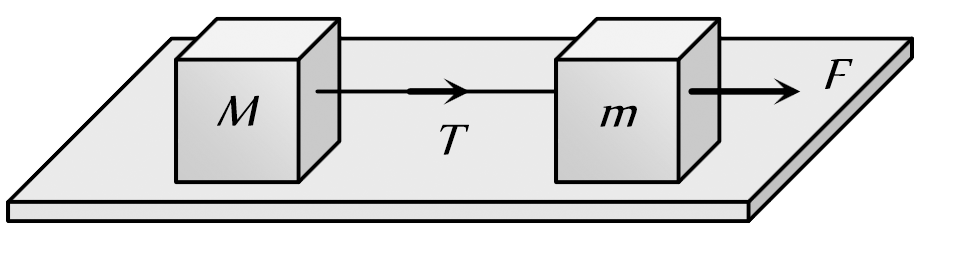 AFMm+MBFM+mCFMmDFmM+m
AFMm+MBFM+mCFMmDFmM+mTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
Ag2Bg3Cg5Dg10
A paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are

View SolutionA particle of mass m and charge q is fastened to one end of a string of length. The other end of the string is fixed to the point O. The whole sytem liles on as frictionless horizontal plane. Initially, the mass is at rest at A. A uniform electric field in the direction shown in then switfched on. Then

View SolutionTwo block of mass 5 kg and 10 kg respectively are connected by a massless string as shown in the figure. The whole system is kept on a frictionless surface. A force of 50 N is applied horizontally as shown in the figure. The tension T in the string will be
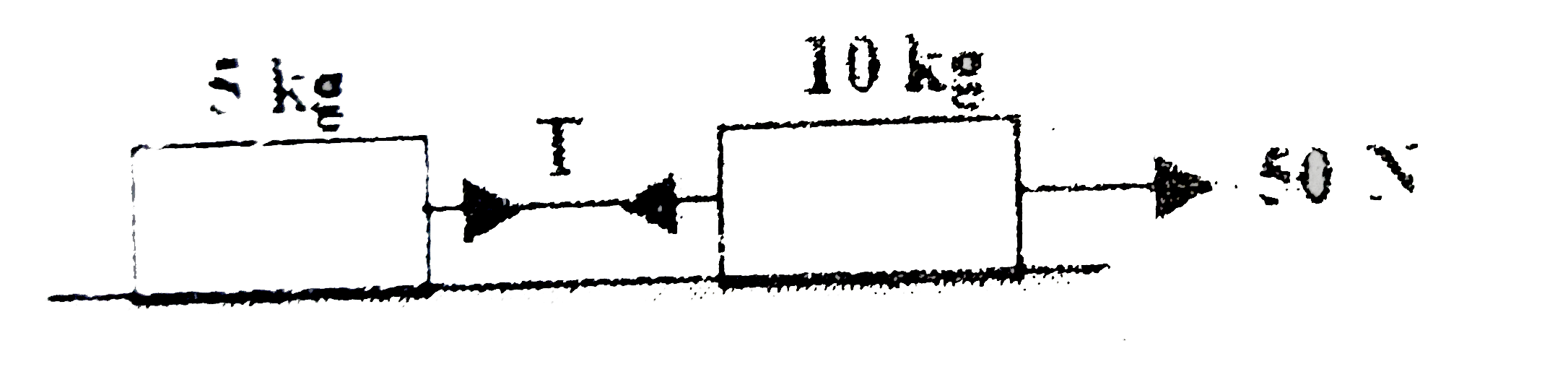
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionTwo identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
View Solution
