Two particles of masses 1.0 kg and 2.0 kg are placed at a separation of 50 cm. Assuming that the only foces acting on the particles are their mutual gravitation find the initial acceleration of hthe two particles.
To solve the problem of finding the initial acceleration of two particles with masses 1.0 kg and 2.0 kg placed 50 cm apart, we will use Newton's law of universal gravitation and Newton's second law of motion. Here’s a step-by-step solution:
Step 1: Identify the Given Data
- Mass of particle 1, m1=1.0kg
- Mass of particle 2, m2=2.0kg
- Separation distance, r=50cm=0.5m
Step 2: Calculate the Gravitational Force
According to Newton's law of universal gravitation, the gravitational force F between two masses is given by:
F=Gm1m2r2
where G is the universal gravitational constant, G=6.67×10−11N m2/kg2.
Substituting the values:
F=(6.67×10−11)×(1.0)×(2.0)(0.5)2
Calculating (0.5)2:
(0.5)2=0.25
Now substituting this back into the equation:
F=(6.67×10−11)×2.00.25
Calculating the force:
F=13.34×10−110.25=53.36×10−11N=5.336×10−10N
Step 3: Calculate the Acceleration of Each Particle
Using Newton's second law, F=m⋅a, we can find the acceleration of each particle.
For particle 1 (mass = 1.0 kg):
a1=Fm1=5.336×10−101.0=5.336×10−10m/s2
For particle 2 (mass = 2.0 kg):
a2=Fm2=5.336×10−102.0=2.668×10−10m/s2
Step 4: Direction of Acceleration
- The acceleration of particle 1 (a1) is directed towards particle 2.
- The acceleration of particle 2 (a2) is directed towards particle 1.
Final Results
- Acceleration of particle 1: a1=5.336×10−10m/s2
- Acceleration of particle 2: a2=2.668×10−10m/s2
- Mass of particle 1, m1=1.0kg
- Mass of particle 2, m2=2.0kg
- Separation distance, r=50cm=0.5m
According to Newton's law of universal gravitation, the gravitational force F between two masses is given by:
F=Gm1m2r2
where G is the universal gravitational constant, G=6.67×10−11N m2/kg2.
F=(6.67×10−11)×(1.0)×(2.0)(0.5)2
Calculating (0.5)2:
(0.5)2=0.25
Now substituting this back into the equation:
F=(6.67×10−11)×2.00.25
Calculating the force:
F=13.34×10−110.25=53.36×10−11N=5.336×10−10N
Using Newton's second law, F=m⋅a, we can find the acceleration of each particle.
a1=Fm1=5.336×10−101.0=5.336×10−10m/s2
a2=Fm2=5.336×10−102.0=2.668×10−10m/s2
- The acceleration of particle 1 (a1) is directed towards particle 2.
- The acceleration of particle 2 (a2) is directed towards particle 1.
- Acceleration of particle 1: a1=5.336×10−10m/s2
- Acceleration of particle 2: a2=2.668×10−10m/s2
Topper's Solved these Questions
- GRAVITATIONBOOK - HC VERMACHAPTER - GRAVITATIONEXERCISE - Worked Out Examples
13 Videos
- GRAVITATIONBOOK - HC VERMACHAPTER - GRAVITATIONEXERCISE - Short Answer
19 Videos
- FRICTIONBOOK - HC VERMACHAPTER - FRICTIONEXERCISE - Exercises
31 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMACHAPTER - HEAT AND TEMPERATUREEXERCISE - Exercise
4 Videos
Similar Questions
Two particles of mass 200 g each are placed at a separation of 10 cm. Assume that the only forces acting on them are due to their gravitational attraction. Find the acceleration of each when they are allowed to move.
View SolutionTwo particles of masses 1kg and 2kg are placed at a distance of 50cm. Find the initial acceleration of the first particle due to gravitational force.
View Solution
Knowledge Check
Two particles of masses 1 kg and 2 kg are placed at a separation of 50 cm find out gravitational force between them
A5.3x10−10NB4.9×10−9NC6.5×10−8ND6.9×x10−7NTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
A2m from 1 kgB2m from 2 kgC1m from 1 kgDnone of theseThree particles, each of the mass m are situated at the vertices of an equilateral triangle of side a. The only forces acting on the particles are their mutual gravitational forces. It is desired that each particle moves in a circle while maintaining the original mutual separation a. Find the initial velocity that should be given to each particle and also the time period of the circular motion. (F=Gm1m2r2)
A2π√a13GmB2π√a23GmC2π√a32GmD2π√a33Gm
Two particle of mass 1 kg and 2 kg are located at x = 0 and x = 3 m. Find the position of their centre of mass.

View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
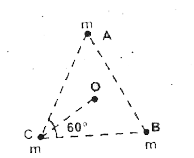
Force acting on particle C, due to particle A and B
View SolutionTwo particles of masses 2m and 3m are placed at separation d on a smooth surface. They move towards each other due to mutual attractive force. Find (a) acceleration of c.m. (b) Velocity of c.m. when separation between particles becomes d/3. ( c) At what distance from the initial position of mass 2m, the particles collide.
View SolutionTwo small bodies of masses 10 kg and 20 kg are kept a distnce 1.0 m apart and released. Assuming that only mutual gravitational force are acting, find the speeds of te particles when the separation decreases to 0.5 m.
View SolutionTwo small bodies of masses 2.00 kg and 4.00 kg are kept at rest at a separation of 2.0 m. Where should a particle of mass 0.10 kg be placed to experience no net gravitational force from these bodies? The particle is placed t this point.What is the gravitational potential energy of the system of three particle with usual reference level?
View Solution
