Two planets revolve with same angular velocity about a star. The radius of orbit of outer planet is twice the radius of orbit of the inner planet. If T is time period of the revolution of outer planet, find the time in which inner planet will fall into the star. If it was suddenly stopped.
A
√23gR11
B
√25gR11
C
v2agR2−R
D
v2a2gR2−R
Text Solution
The correct Answer is:B
To=2πrω,T1=2πr2ω=To2
Consider an imaginary comet moving along an ellipse. The extreme points of this ellipse are located on orbit of inner planet and the star, sem-major axis of orbit of such comet will be half of the semi-major axis of the inner planet's orbit. According to Kepler's law. if T' is the time period of the comet.
T'2(r/4)3=T21(r/2)3
T'2=864T21=T2032(∵T1=T0/2)
T'=T4√2
(T'/2) represents time in which inner planet will fall into star.
(T'2)=T8√2=T√216
|
Topper's Solved these Questions
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Assertion Reasoning
16 Videos
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - NEET Questions
42 Videos
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Motion Of Satellite
33 Videos
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - Chapter Test
30 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Chapter Test
29 Videos
Similar Questions
Knowledge Check
The radius of orbit of a planet is two times that of the earth. The time period of planet is
A4.2 yearsB2.8 yearsC5.6 yearsD8.4 yearsThe period of a planet around sun is 27 times that of earth the ratio of radius of planet orbit to the radius of earth's orbit is
A4B9C64D27Orbit of a planet around a star is
Aan ellipseBa circleCa parabolaDa byperbola
What are inner planets and outer planets ? Name them .
View SolutionOrbit of a planet around a star is
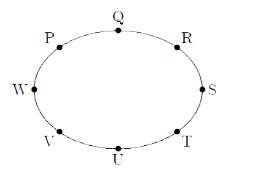
View SolutionA planet travels in an elliptical orbit about a star as shown. At what pair of points is the speed of the planet the same?
View SolutionIf a time period of revolution of a satellite around a planet in a circular orbit of radius r is T,then the period of revolution around planet in a circular orbit of radius 3r will be
View SolutionIf a and b are the nearest and farthest distances of a planet from the sun and the planet is revolving in an elliptical orbit, then square of the time period of revolution of that planets is directly proportional to
View Solution
