Two point charges q1=q2=2μC are fixed at x1=+3m and x2=−3m as shown in figure. A third particle of mass 1 g and charge q3=−4μC are released from rest at y=4.0m.Find the speed of the particle as it reaches the origin.
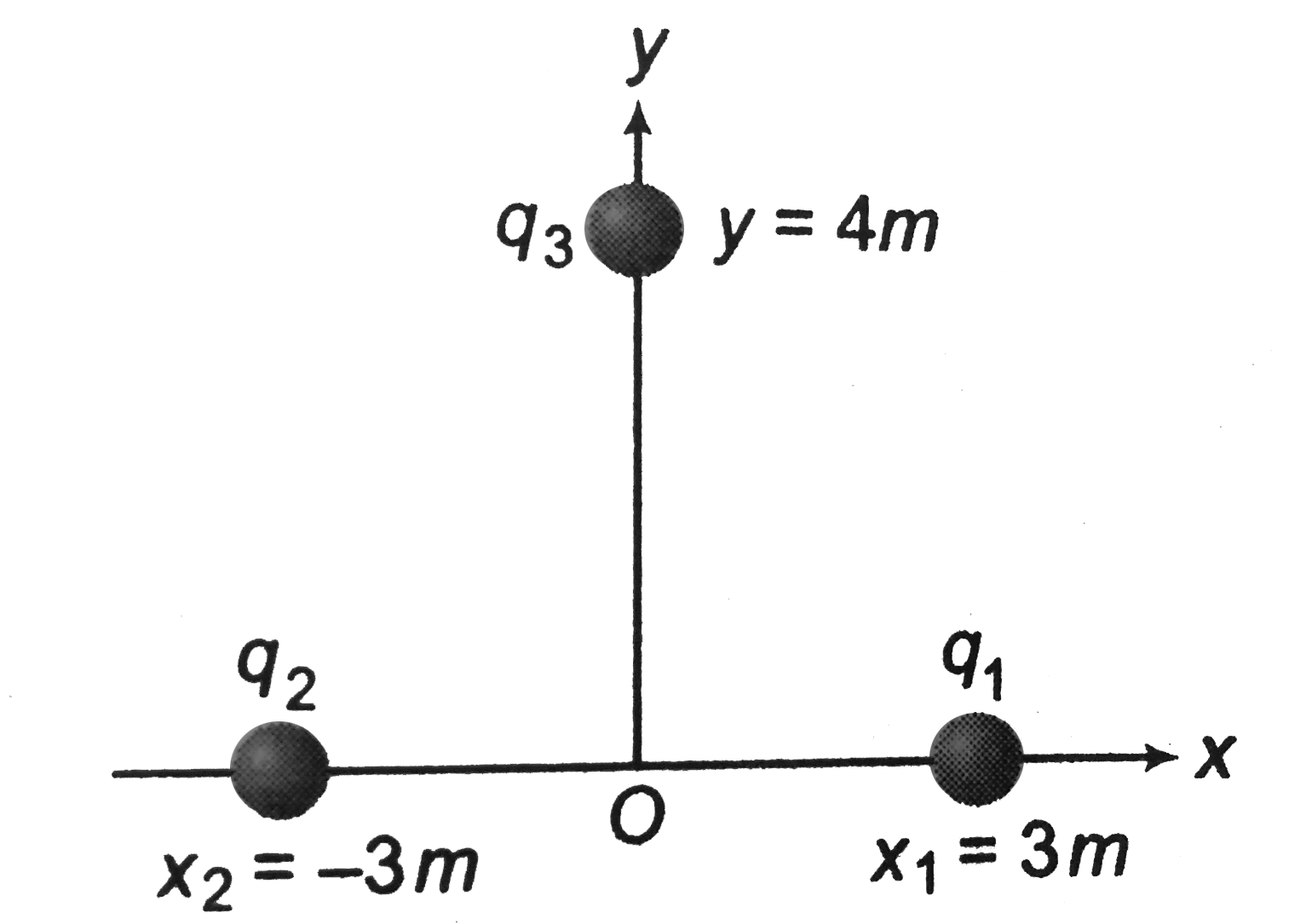
Here the charge q3 is attracted toward q1 and q2 both so the net force on q3 is toward the origin As only force acting is conservative we can use conservation of mechanical energy let v be the speed of particle at origin. From energy of conservation principle we get
Ui+Ki=U+K
or 14πε0[q3q2(r32)i+q3q1(r32)i+q2q1(r21)i]+0
=14πε0[q3q2(r32)f+q3q1(r31)f+q2q1(r21)f]+12mv2
Here (r21)i=(r21)f substituting the proper values
9×109[(−4)(2)5+(−4)(2)3]×10−12+12×10−12+12×10−3v2
or (9×10−3)(−165)=(×10−3)(−163)+12×10−3v2
or 9×10−3(16)(215)=12×10−3v2
or v=6.2=6ms−1
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Fill in the blanks10videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False Type5videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type94videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Question Bank4videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
Similar Questions
A particle of mass 100 gm and charge 2μC is released from a distance of 50 cm from a fixed charge of 5μC. Find the speed of the particle when its distance from the fixed charge becomes 3 m.
View SolutionA particle of mass 100 gm and charge 2μC is released from a distance of 50 cm from a fixed charge of 5μC. Find the speed of the particle when its distance from the fixed charge becomes 3 m.
View Solution
Knowledge Check
- Question 1 - Select One
The value of charge q1,q2andq3 as shown in the figure are
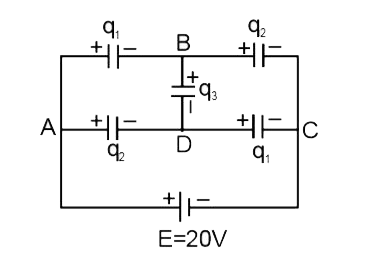 Aq1=32μC,q2=24μC,q3=−8μCBq1=48μc,q2=16μC,q3=+8μCCq1=32μC,q2=24μC,q3=+8μCDq1=3μC,q2=4μC,q3=+2μC
Aq1=32μC,q2=24μC,q3=−8μCBq1=48μc,q2=16μC,q3=+8μCCq1=32μC,q2=24μC,q3=+8μCDq1=3μC,q2=4μC,q3=+2μC - Question 2 - Select One
Two circular rings A and B each of radius a = 30 cm are placed coaxially with their axis horizontal in a uniform electric field E=105NC−1 directed vertically upward as shown in figure. Distance between centers of the rings A and B (CAandCB)is40cm. Ring A has positive charge qA=10μC and B has a negative charge qB=−20μC. A particle of mass m and charge q=10μC is released from rest at the center of ring A. If particle moves along CACB, then
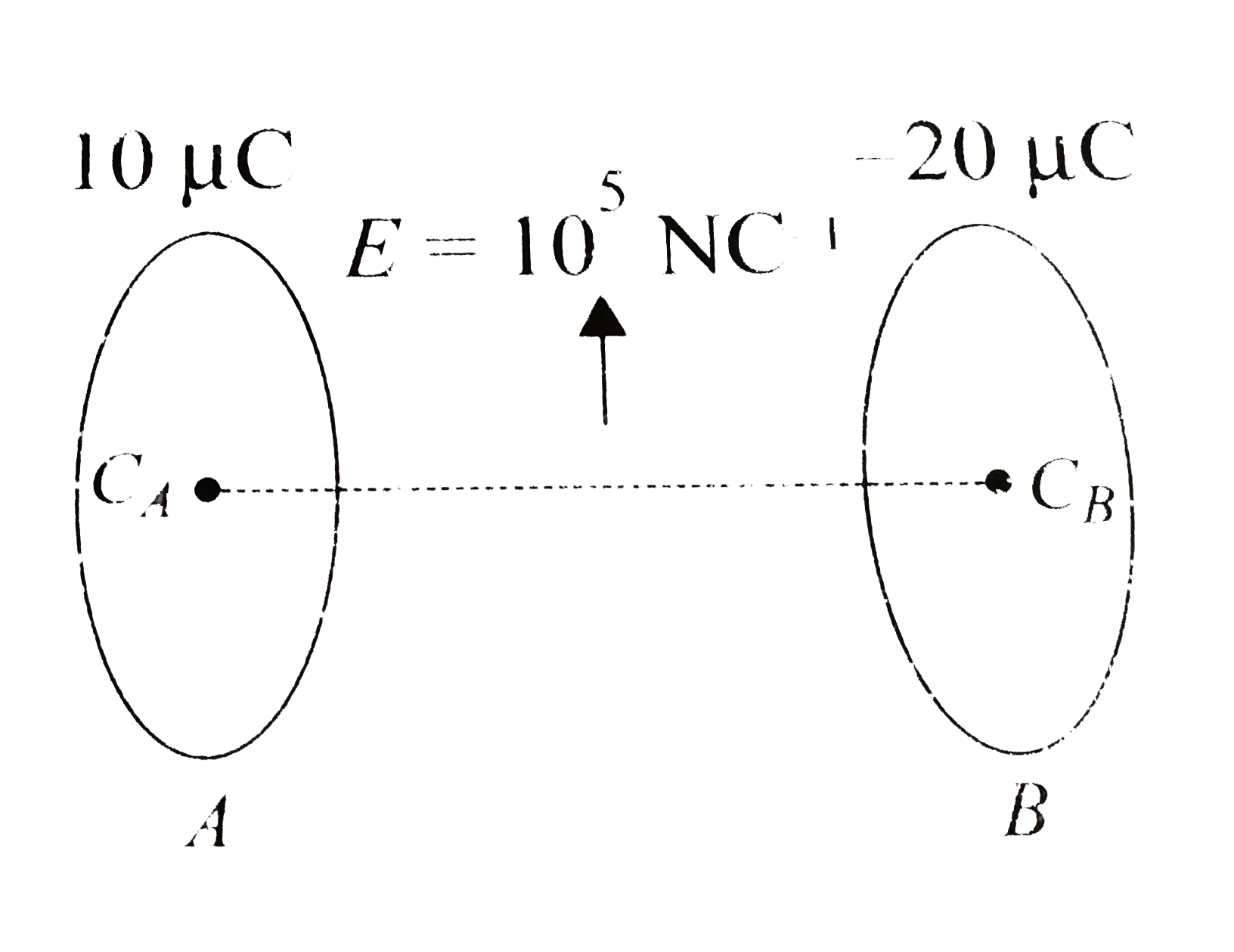
Speed of particle when it reaches at center of B isA6√2m/sB12√2m/sC2√6m/sD4√6m/s - Question 3 - Select One
A charged particle of mass m and charge q is released from rest the position (x0,0) in a uniform electric field E0ˆj. The angular momentum of the particle about origin.
Ais zeroBis constantCincreases with timeDdecreases with time
Two equal positive charges , Q , are fixed at points (0,d) and (0,−d) on the y-axis. A charged particle having charge −q and mass m is released from rest at point (d,0) on the x-axis . Discuss the motion of charged particle.
View SolutionFour identical positive point charges Q are fixed at the four corners of a square of side length l. Another charged particle of mass m and charge +q is projected towards centre of square from a large distance along the line perpendicular to plane of square. The minimum value of initial velocity v0 (in m/s) required to cross the square is ?
(m=1gm,l=4√2m,Q=1μc,q=0.5μc)
 View Solution
View SolutionIdentical 50μC charges are fixed on an x axis at x=+±2.0 m. A particle of charge q=15μC is then released from rest at a point on the positive part of they axis. Due to the symmetry of the situation, the particle moves along the y axis and has kinetic energy 1.2 J as it passes through the pointx=0,y=4.0m. (a) What is the kinetic energy of the particle as it passes through the origin? (b) At what negative value of y will the particle momentarily stop?
View SolutionA block 'A' of charge q1 is fixed and second block of mass m and charge q2 is allowed to free on the floor findout the range of q2 for which the particle is at rest.
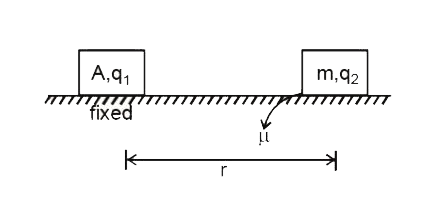 View Solution
View SolutionAs charge q=1μC is placed at point (1m,2m,4m). Find the electric field at point P(0,−4m,3m)
View Solution

