Two small balls A and B of positive charge Q each and masses m and 2m respectively are connected by a non conducting light rod of length L. This system is released in a uniform electric field of strength E as shown. Just after the release (assume no other force acts on the system)
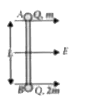
rod has zero angular acceleration
rod has angular acceleration in anti-clockwise direction.
acceleration of point A is towards right
acceleration of point A is towards right.
The correct Answer is:D
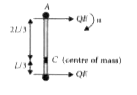
Resultant force on arrangement is 2QE, thus acceleration of centre of mass is given by
(towards right)
As per conservation of angular momentum
(clockwise)
From constrant equation, we get
(towards right)
Topper's Solved these Questions
- MODEL TEST PAPER 1 BOOK - MTG-WBJEECHAPTER - MODEL TEST PAPER 1 EXERCISE - PHYSICS (Category) 3 : Single Option correct type (2 mark)
5 Videos
- MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTIONBOOK - MTG-WBJEECHAPTER - MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTIONEXERCISE - WB-JEE Previous years questions
17 Videos
Similar Questions
A protons of mass m charge 2 e is released from rest in a uniform electric field of strength E .The time taken by it to travel a distance d in the field is..
View SolutionA charge of mass .m. charge .2e. is released from rest in a uniform electric field of strength .E.. The time taken by it to travel a distance .d. in the field is
View Solution
Knowledge Check
A protons of mass m charge c is released form rest in a uniform electric field of strength E .The time taken by it to travel a distance d in the field is
A√2demEB√2dmEeC√2dEmeD√2dEedmAn electron of mass m and charge q is accelerated from rest in a uniform electric field of strength E. The velocity acquired by it as it travels a distance l is
A√2EqlmB√2ElmlC√2EmqlD√Eqml
Two point masses of mass m and equal and opposite charge of magnitude q are attached on the corners of a non-conducting uniform rod of mass m and the system is released from rest in uniform electric field E as shown in figure from θ=53∘

(i) Find angular acceleration of the rod just after releasing
(ii) What will be angular velocity of the rod when it passes through stable equilibrium.
(iii) Find work required to rotate the system by 180∘.
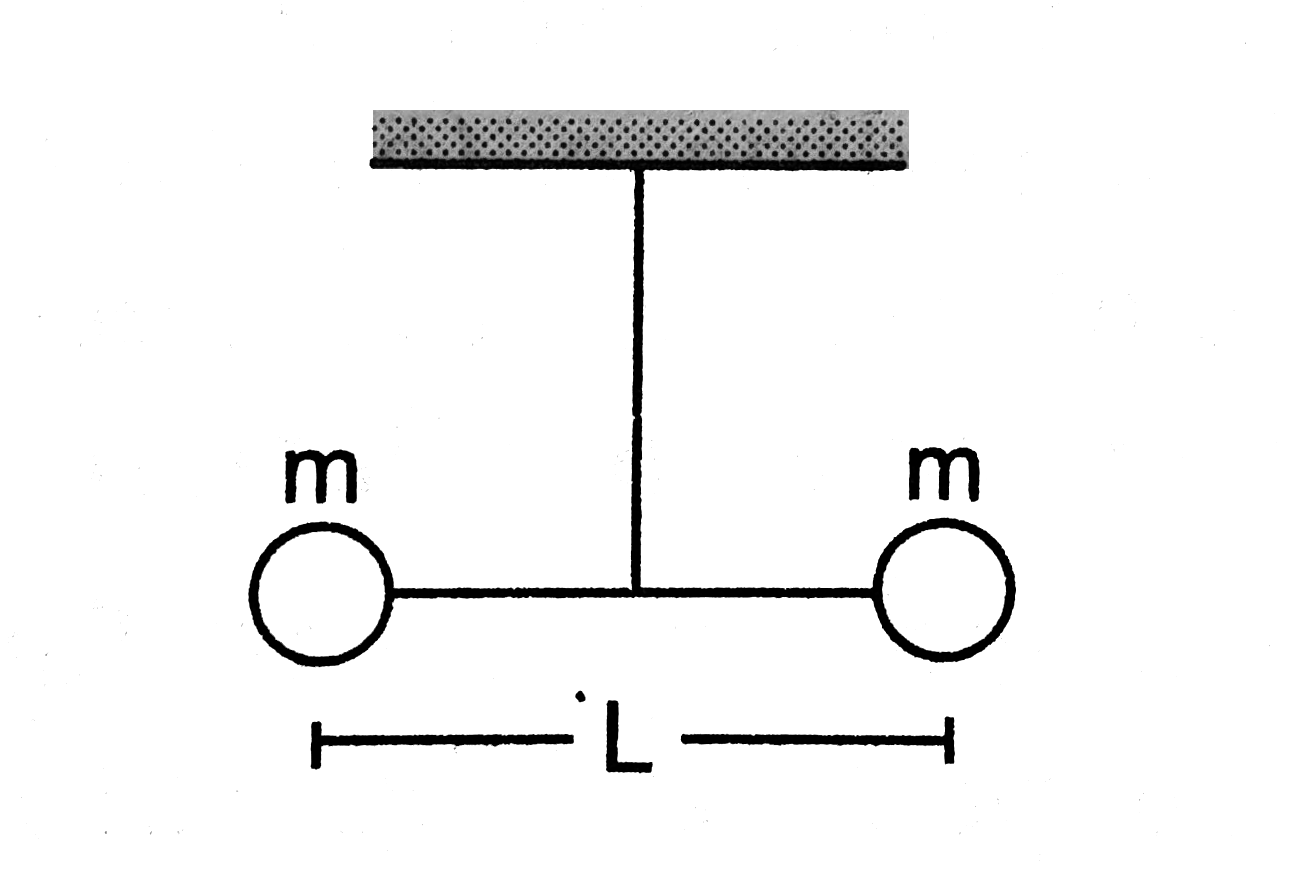
View SolutionTwo small balls, each of mass m are connected by a light rigid rod of length L. The system is suspended from its centre by a thin wire of torsional constant k. The rod is rotated about the wire through an angle θ0 and released. Find the tension in the rod as the system passes through the mean position.
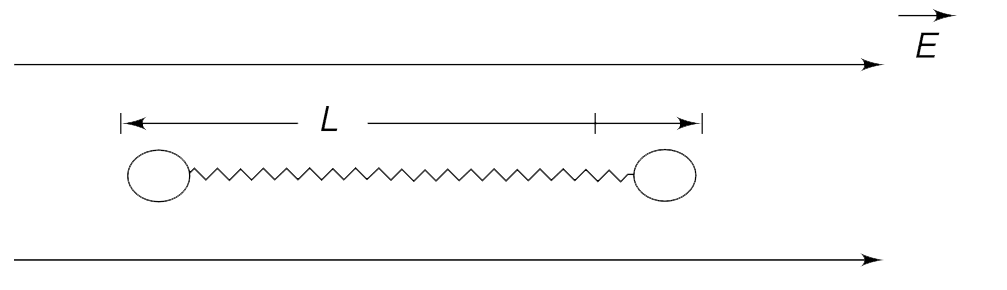
View SolutionTwo small identical conducting balls each of radius r and mass m are placed on a frictionless horizontal table, connected by a light conducting spring of force constant K and un-deformed length L (L gtgt r). A uniform electric field of strength E is switched on in horizontal direction parallel to the spring. (a) How much charge will appear on the two balls when they are at separation L. (b) The system fails to oscillate if K lt K0. Find K0. (c) Assuming K=2K0, find the time period of oscillation after the electric field is switched on.
View SolutionA simple pendulum consists of a small sphere of mass m suspended by a thread of length l. The sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically downwards. Finds the period of oscillation of the pendulum due to the electrostatic force acting on the sphere, neglecting the effect of the gravitational force.
View SolutionA simple pendulum consists of a small sphere of mass m suspended by a thread of length l. the sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically upwards. With what period will the pendulum oscillate if the electrostatic force acting on the sphere is less than the gravitational force?
View SolutionA particle of mass .m. and charge q is placed at rest in a uniform electric field E and then released. The K.E. attained by the particle after moving a distance y is
View Solution
