Two small rings each of mass ‘m’ are connected to a block of same mass ‘m’ through inextensible light strings. Rings are constrained to move along a smooth horizontal rod. Initially system is held at rest (as shown in figure) with the strings just taut. Length of each string is ‘l’. The system is released from the position shown. Find the speed of the block (v) and speed of the rings (u) when the strings make an angle of theta=60^(@)withvertical.(Takeg = 10 m//s^2)
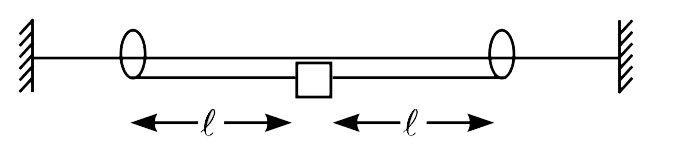
The correct Answer is:u=√gl5.V=√3gl5
Step by step video, text & image solution for Two small rings each of mass ‘m’ are connected to a block of same mass ‘m’ through inextensible light strings. Rings are constrained to move along a smooth horizontal rod. Initially system is held at rest (as shown in figure) with the strings just taut. Length of each string is ‘l’. The system is released from the position shown. Find the speed of the block (v) and speed of the rings (u) when the strings make an angle of theta=60^(@) with vertical. (Take g = 10 m//s^2) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The pulley is light and smooth: the strings are inextensible and light. The system is released from rest, find the acceleration of each block, tensions in the strings and reaction in pulley.

View SolutionIn the system shown in figure, the block A is released from rest. Find
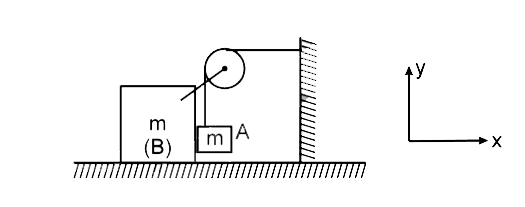
Tension in the string.
View Solution
Knowledge Check
Two small rings each of mass 'm' are connected to a block of same mass 'm' through inextensible light strings. Rings are constrained to move along a smooth horizontal rod. Initially system is held at rest (as shown in figure) with the strings make an angle of θ=60∘ with vertical is. (Take g=10m/s2)
 A√3gl5B√gl5C√5gl4DNone of these
A√3gl5B√gl5C√5gl4DNone of theseTwo small rings, each of mass 'm', are connected to the block of same mass 'm' through an inextensible massless string of length 'l'. Rings are constrained to move over smooth rod AB. Initially, the system is held at rest as shown in Fig. Let a and v be the velocities of ring and block, respectively when string makes an angle 60∘ with the vertical.
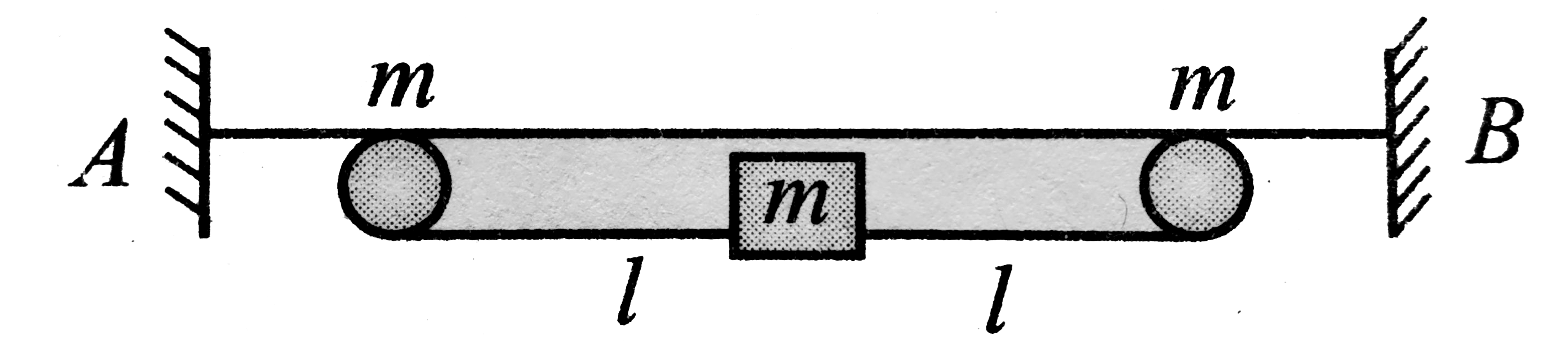 Au=√gl5Bu=√8gl5Cv=√3glDv=√3gl5
Au=√gl5Bu=√8gl5Cv=√3glDv=√3gl5Two beads of mass 2m and m, connected by a rod of length l and of negligible mass are free to move in a smooth vertical circular wire frame of radius l as shown. Initially the system is held in horizontal position ( Refer figure )

If the rod is replaced by a massless string of length l and the system is released when the string is horizontal then :AMass 2m will arrive earlier at the bottomBMass m will arrive earlier at the bottom.CBoth the masses will arrive together but different speeds.DBoth the masses will arrive together with same speeds.
Two blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is

View SolutionThe system shown in figure is released is released from rest . Find acceleration of different string blocks and tenson in different strings.

View SolutionA rod and a block are of same mass. Initially rod is in horizontal position. What will be acceleration of tip of the rod just after the system is released from this position shown in figure.
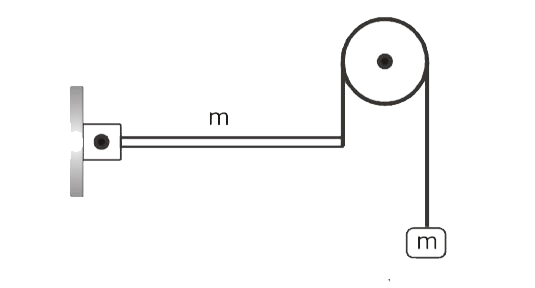
View SolutionA wheel of moment of inertia I and rdius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.

View SolutionA particle of mass 2m is connected by an inextensible string of length 1.2m to a ring of mass m which is free to slide on a horizontal smooth rod. Initially the ring and the particle are at the same level with the string taut. Both are then released simultaneously. The distance in meter moved by the ring when the string becomes veritcal is :-
View Solution
