Two solenoids are part of the spark coil of an automobile. When the current in one solenoid fails from 6.0 A to zero in 2.5 ms, an emf of 31 kV is induced in the other solenoid. What is the mutual inductance M of the solenoids?
To find the mutual inductance M of the two solenoids given the problem, we can follow these steps:
Step 1: Understand the relationship between induced EMF and mutual inductance
The induced electromotive force (EMF) in solenoid 2 due to the change in current in solenoid 1 is given by the formula:
E2=−MdI1dt
where:
- E2 is the induced EMF in solenoid 2,
- M is the mutual inductance,
- dI1dt is the rate of change of current in solenoid 1.
Step 2: Identify the given values
From the problem, we have:
- E2=31kV=31×103V
- The current in solenoid 1 changes from 6.0A to 0A in 2.5ms=2.5×10−3s.
Step 3: Calculate the rate of change of current dI1dt
The change in current ΔI1 is:
ΔI1=Ifinal−Iinitial=0−6.0=−6.0A
The rate of change of current is:
dI1dt=ΔI1Δt=−6.0A2.5×10−3s=−2400A/s
Step 4: Substitute the values into the mutual inductance formula
Now, substituting the values into the mutual inductance formula:
E2=−MdI1dt⟹M=−E2dI1dt
Substituting the known values:
M=−31×103V−2400A/s=31×1032400
Step 5: Calculate the mutual inductance
Now, performing the calculation:
M=31×1032400≈12.9167H
Rounding this to two decimal places gives:
M≈12.92H≈13H
Final Answer
Thus, the mutual inductance M of the solenoids is approximately 13H.
---
The induced electromotive force (EMF) in solenoid 2 due to the change in current in solenoid 1 is given by the formula:
E2=−MdI1dt
where:
- E2 is the induced EMF in solenoid 2,
- M is the mutual inductance,
- dI1dt is the rate of change of current in solenoid 1.
From the problem, we have:
- E2=31kV=31×103V
- The current in solenoid 1 changes from 6.0A to 0A in 2.5ms=2.5×10−3s.
The change in current ΔI1 is:
ΔI1=Ifinal−Iinitial=0−6.0=−6.0A
The rate of change of current is:
dI1dt=ΔI1Δt=−6.0A2.5×10−3s=−2400A/s
Now, substituting the values into the mutual inductance formula:
E2=−MdI1dt⟹M=−E2dI1dt
Substituting the known values:
M=−31×103V−2400A/s=31×1032400
Now, performing the calculation:
M=31×1032400≈12.9167H
Rounding this to two decimal places gives:
M≈12.92H≈13H
Thus, the mutual inductance M of the solenoids is approximately 13H.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
45 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
13 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHECKPOINTS
9 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
- ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT EXERCISE - Practice Questions (Integer)
7 Videos
Similar Questions
Two toroidal solenoids are wound around the same pipe so that the magnetic field of one passes through the turns of the other. Solenoid 1 has 700 turns and solenoid 2 has 400 turns. When the current in solenoid 1 is 6.52A, the average flux through each turn of solenoid 2 is 0.0320Wb.
(a) What is the mutual inductance of the pair of solenoids?
(b) When the current in solenoid 2 is 2.54A, what is the average flux through each solenoid 1?
View SolutionA current l = 1.5 A is flowing through a long solenoid of diameter 3.2 cm, having 220 turns per cm. At its centre, a 130 turn closely packed coil of diameter 2.1 cm is placed such that the coil is coaxial with the long solenoid. The current in the solenoid is reduced to zero at a steady rate in 25 ms. What is the magnitude of emf induced in the coil while the current in the solenoid is changing?
View Solution
Knowledge Check
If a rate of change of current of 4 As−1 induces an emf of 20 mV in a solenoid, the self inductance of the solenoid is
A5 mHB80 mHC0.25 mHDzeroThe average self-induced emf in a 25mH solenoid when the current in it falls from 0.2A to 0A in 0.01 second, is
A0.05VB0.5VC500VD50VAn e.m.f of 40 mV is induced in a solenoid, when the current in it changes at the rate of 2A/s. The self inductance of the solenoid is
A5 mHB10 mHC20 mHD40 mH
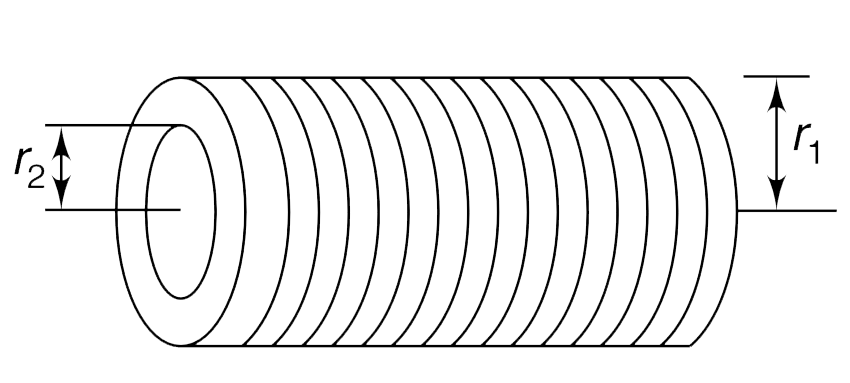
Two long co-axial solenoids have radii, and number of turns per unit length equal to r1,r2 and n1,n2 respectively where suffix 1 refers to the outer solenoid and 2 refers to the inner solenoid. Length of both is l. The current in the outer solenoid is made to grow as I1=kt where t is time. Resistance of the wire used in inner solenoid is R. Write the current induced in the inner solenoid assuming that it is shorted.
View SolutionThrough a long solenoid of diameter 4.1 cm, having 100 turns per cm, a current I = 1A is flowing. At its centre, a 60 turns closely packed coil of diameter 3.1 cm si placed such that the coil is coaxial with the long solenoid. The current in the solenoid is reduced to zero at a steady rate in 10 ms. What is the magnitude of emf induced in the coil while the current in the solenoid is changing?
View SolutionA long solenoid has 800 turns per meter length of solenoid. What is the magnatic induction at the end of the solenoid if it carries a current of 2.5 A?
View SolutionA short solenoid of length 4 cm, radius 2 cm and 100 turns is placed inside and on the axis of a long solenoid of length 80 cm and 1500 turns. A current of 3 A flows through the short solenoid. The mutual inductance of two solenoid is
View SolutionA 0.100 m long solenoid has a radius of 0.050 m and 1.50×104 turns. The current in the solenoid changes at a rate of 6.0 A/s. A conducting loop of radius 0.0200 m is placed at the center of the solenoid with its axis the same as that of the solenoid as shown.
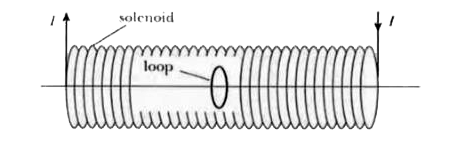
Determine the mutual inductance of this combination.
View Solution
