Two spherical nuclei have mass number 216 and 64 with their radii R1andR2 respectively. The ratio, R1R2 is equal to
3:2
1:3
1:2
2:3
The correct Answer is:A
To solve the problem of finding the ratio of the radii of two spherical nuclei with mass numbers 216 and 64, we can follow these steps:
Step 1: Understand the formula for the radius of a nucleus
The radius R of a nucleus can be expressed in terms of its mass number A using the formula:
R=R0A1/3
where R0 is a constant approximately equal to 1.2×10−15 meters.
Step 2: Write the expressions for the radii of the two nuclei
Let R1 be the radius of the nucleus with mass number A1=216 and R2 be the radius of the nucleus with mass number A2=64. We can write:
R1=R0(216)1/3
R2=R0(64)1/3
Step 3: Find the ratio of the radii
To find the ratio R1R2, we can substitute the expressions for R1 and R2:
R1R2=R0(216)1/3R0(64)1/3
The R0 cancels out:
R1R2=(216)1/3(64)1/3=(21664)1/3
Step 4: Simplify the fraction
Now, we simplify 21664:
21664=278=(32)3
Thus,
R1R2=(32)1=32
Step 5: State the final answer
Therefore, the ratio of the radii R1R2 is:
R1R2=32
Final Answer
The ratio R1R2 is 32.
---
The radius R of a nucleus can be expressed in terms of its mass number A using the formula:
R=R0A1/3
where R0 is a constant approximately equal to 1.2×10−15 meters.
Let R1 be the radius of the nucleus with mass number A1=216 and R2 be the radius of the nucleus with mass number A2=64. We can write:
R1=R0(216)1/3
R2=R0(64)1/3
To find the ratio R1R2, we can substitute the expressions for R1 and R2:
R1R2=R0(216)1/3R0(64)1/3
The R0 cancels out:
R1R2=(216)1/3(64)1/3=(21664)1/3
Now, we simplify 21664:
21664=278=(32)3
Thus,
R1R2=(32)1=32
Therefore, the ratio of the radii R1R2 is:
R1R2=32
The ratio R1R2 is 32.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two soap bubbles A and B have radii r1andr2 respectively. If r1<r2 than the excess pressure inside
Abubbles A and B will be equalBbubbles A will be less than that in bubbles BCbubbles A will be greater than that in bubble BDbubbles A and B will be zero.
Two concentric shells have masses M and m and their radii are R and r, respectively, where R>r. What is the gravitational potential at their common centre?
View SolutionA planet of mass M, has two natural satellites with masses m1 and m2. The radii of their circular orbits are R1 and R2 respectively. Ignore the gravitational force between the satellites. Define v1,L1,K1 and T1 to be, respectively, the orbital speed, angular momentum, kinetic energy and time period of revolution of satellite 1 , and v2,L2,K2 and T2 to be he corresponding quantities of satellite 2. Given m1/m2=2 and R1/R2=1/4, match the ratios in List-I to the numbers in List-II.
View SolutionTwo reactions R2andR2 have identical pre - exponential factors. Activations enery of R1 exceeds that of R2 by 10 kJ mol−1 . If k1andk2 are rate constants for rate constants for reactions R1andR2
respectively at 300k , then In (k2k1)is equal to (R=8.314Jmol−1K−1)
View SolutionTwo cars having masses m1andm2 move in circles of radii r1andr2 respectively. If they complete the circle is equal time the ratio of their angular speeds is ω1ω2 is
View SolutionAssertion : Two spherical shells have masses m1andm2. Their radii are r1andr2. Let r be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for O<r<r1
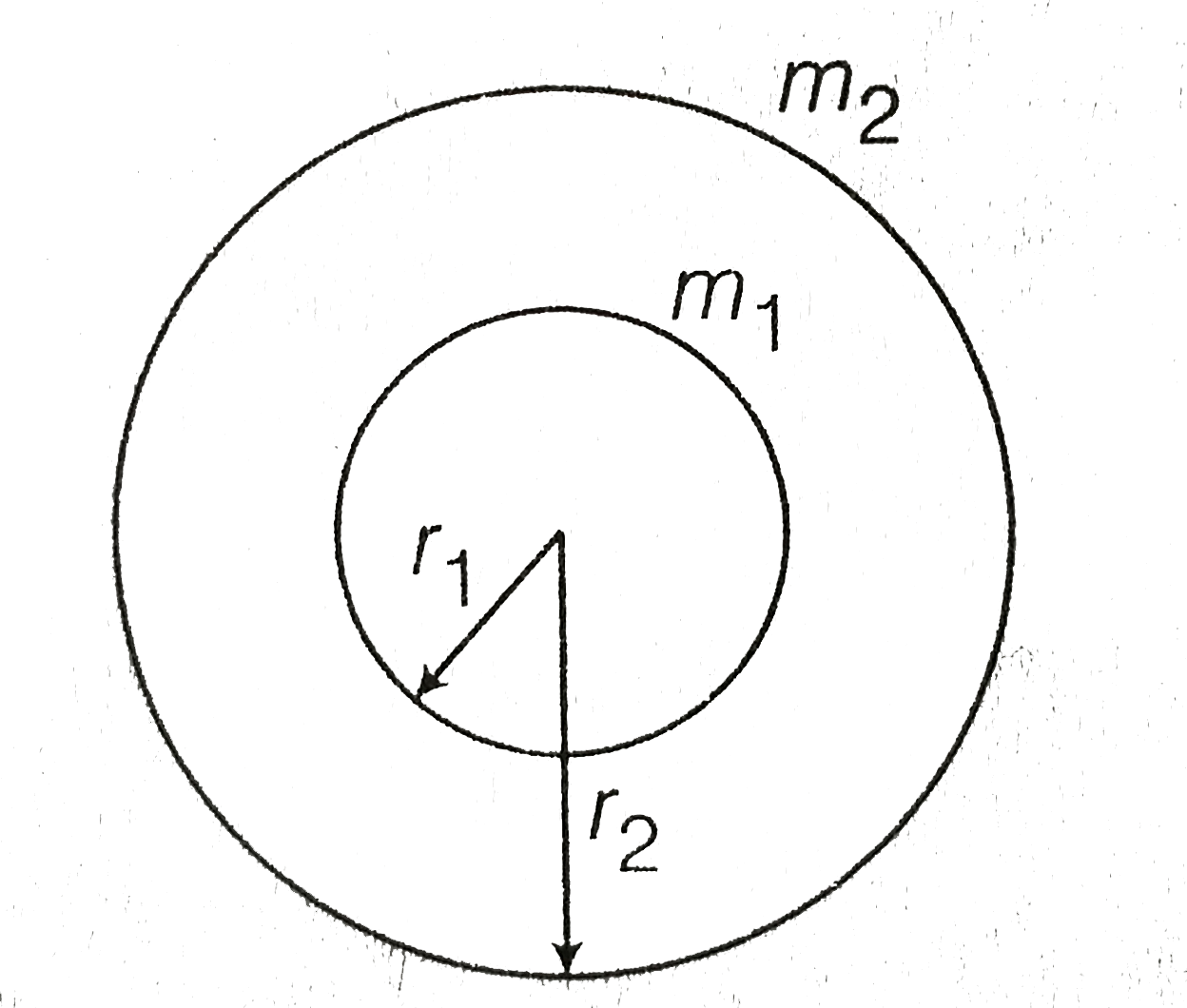
Reason : In the region r1<r<r2, gravitational field strength due to m2 is zero. But gravitational potential due to m2 is constant (but non-zero).
View SolutionTwo planets of masses M and M2 have radii R and R2 respectively. If ratio of escape velocities from their surfaces v1v2 is n4 , then find n :
View SolutionTwo loops P and Q are made from a uniform wire. The radii of P and Q are R1 and R2, respectively, and their moments of inertia about their axis of rotation are I1 and I2, respectively. If I1I2=4, then R2R1 is
View Solution
