Two thermally insulated vessel 1 and 2 are filled with air at temperature (T1T2),volume(V1V2) and pressure (P1P2) respectively. If the valve joining the two vessels is opened, the temperature inside the vessel at equilibrium will be
T1+T2
(T1+T2)/2
T1T2(V1+V2)p1V1T2+p2V2T1.
T1T2(p1V1+p2V2)p1V1T2+p2V2T1.
The correct Answer is:C
To find the equilibrium temperature T when two thermally insulated vessels are connected, we can use the principles of thermodynamics. Here’s a step-by-step solution:
Step 1: Understand the System
We have two thermally insulated vessels (1 and 2) filled with air at different temperatures T1 and T2, volumes V1 and V2, and pressures P1 and P2. Since they are thermally insulated, no heat is exchanged with the surroundings.
Step 2: Apply the First Law of Thermodynamics
The First Law of Thermodynamics states:
ΔQ=ΔU+ΔW
Since the vessels are insulated, ΔQ=0. Also, since the volume is constant, ΔW=0. Therefore:
0=ΔU+0⟹ΔU=0
Step 3: Express Internal Energy Change
The change in internal energy for an ideal gas can be expressed as:
ΔU=n1CVT1+n2CVT2
At equilibrium, the total internal energy before and after the valve is opened must be equal:
n1CVT1+n2CVT2=(n1+n2)CVT
Step 4: Simplify the Equation
Since CV is a constant and appears in all terms, we can cancel it out:
n1T1+n2T2=(n1+n2)T
Step 5: Express Number of Moles
Using the ideal gas law, we can express the number of moles n1 and n2 as:
n1=P1V1RT1,n2=P2V2RT2
Step 6: Substitute Values
Substituting these expressions into the energy balance equation:
P1V1RT1T1+P2V2RT2T2=(P1V1RT1+P2V2RT2)T
Step 7: Simplify Further
This simplifies to:
P1V1R+P2V2R=(P1V1RT1+P2V2RT2)T
Multiplying through by R:
P1V1+P2V2=(P1V1T1+P2V2T2)T
Step 8: Solve for Equilibrium Temperature
Rearranging gives:
T=T1T2(P1V1+P2V2)P1V1T2+P2V2T1
Final Answer
Thus, the equilibrium temperature T is given by:
T=T1T2(P1V1+P2V2)P1V1T2+P2V2T1
We have two thermally insulated vessels (1 and 2) filled with air at different temperatures T1 and T2, volumes V1 and V2, and pressures P1 and P2. Since they are thermally insulated, no heat is exchanged with the surroundings.
The First Law of Thermodynamics states:
ΔQ=ΔU+ΔW
Since the vessels are insulated, ΔQ=0. Also, since the volume is constant, ΔW=0. Therefore:
0=ΔU+0⟹ΔU=0
The change in internal energy for an ideal gas can be expressed as:
ΔU=n1CVT1+n2CVT2
At equilibrium, the total internal energy before and after the valve is opened must be equal:
n1CVT1+n2CVT2=(n1+n2)CVT
Since CV is a constant and appears in all terms, we can cancel it out:
n1T1+n2T2=(n1+n2)T
Using the ideal gas law, we can express the number of moles n1 and n2 as:
n1=P1V1RT1,n2=P2V2RT2
Substituting these expressions into the energy balance equation:
P1V1RT1T1+P2V2RT2T2=(P1V1RT1+P2V2RT2)T
This simplifies to:
P1V1R+P2V2R=(P1V1RT1+P2V2RT2)T
Multiplying through by R:
P1V1+P2V2=(P1V1T1+P2V2T2)T
Rearranging gives:
T=T1T2(P1V1+P2V2)P1V1T2+P2V2T1
Thus, the equilibrium temperature T is given by:
T=T1T2(P1V1+P2V2)P1V1T2+P2V2T1
Topper's Solved these Questions
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 More Than One Correct
7 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Subjective
9 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 1 Subjective
48 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary
30 Videos
- UNIT AND DIMENSIONSBOOK - DC PANDEY ENGLISHCHAPTER - UNIT AND DIMENSIONSEXERCISE - Assertion And Reason
2 Videos
Similar Questions
Two containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionTwo chemically non-reactive gases are separately contained in two vessels of same capacity at pressure P1, and P2, respectively. If two vessels are connected, the total pressure of gaseous mixture will be
View SolutionTwo chemically non-reactive gases are separately contained in two vessels of same capacity at pressure P1 and P2 respectively. If two vessels are connected, the total pressure of gaseous mixture will
View SolutionA thermally insulated vessels contains two liquids with initial temperature T1 and T2 and specific heats C0 and 2C0, separted by a non conducting partition. The partition is removed, and the difference between the initial temperature of one of the liquids and the temperature T established in the vessel turns out to be equal to half the difference between the initial temperatures of the liquids. Determine the ratio of M1/M2 of the masses of the liquids.

View SolutionThe velocities of sound in an ideal gas at temperature T1andT2 K are found to be V1andV2 respectively. If ther.m.s velocities of the molecules of the same gas at the same temperatures T1andT2 are v1andv2 respectively then
View SolutionThe velocities of sound in an ideal gas at temperature T1andT2 K are found to be V1andV2 respectively. If ther.m.s velocities of the molecules of the same gas at the same temperatures T1andT2 are v1andv2 respectively then
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
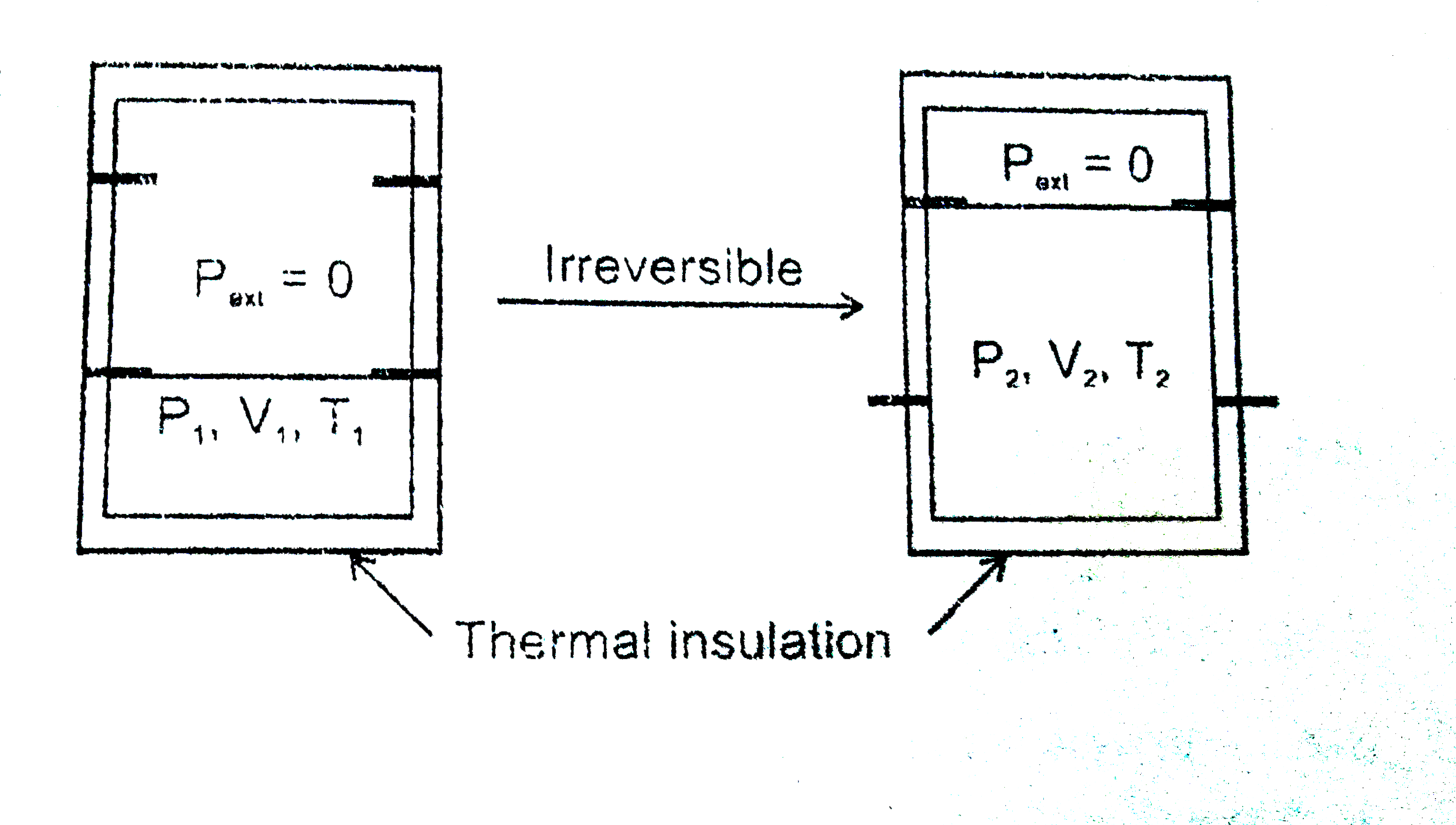
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
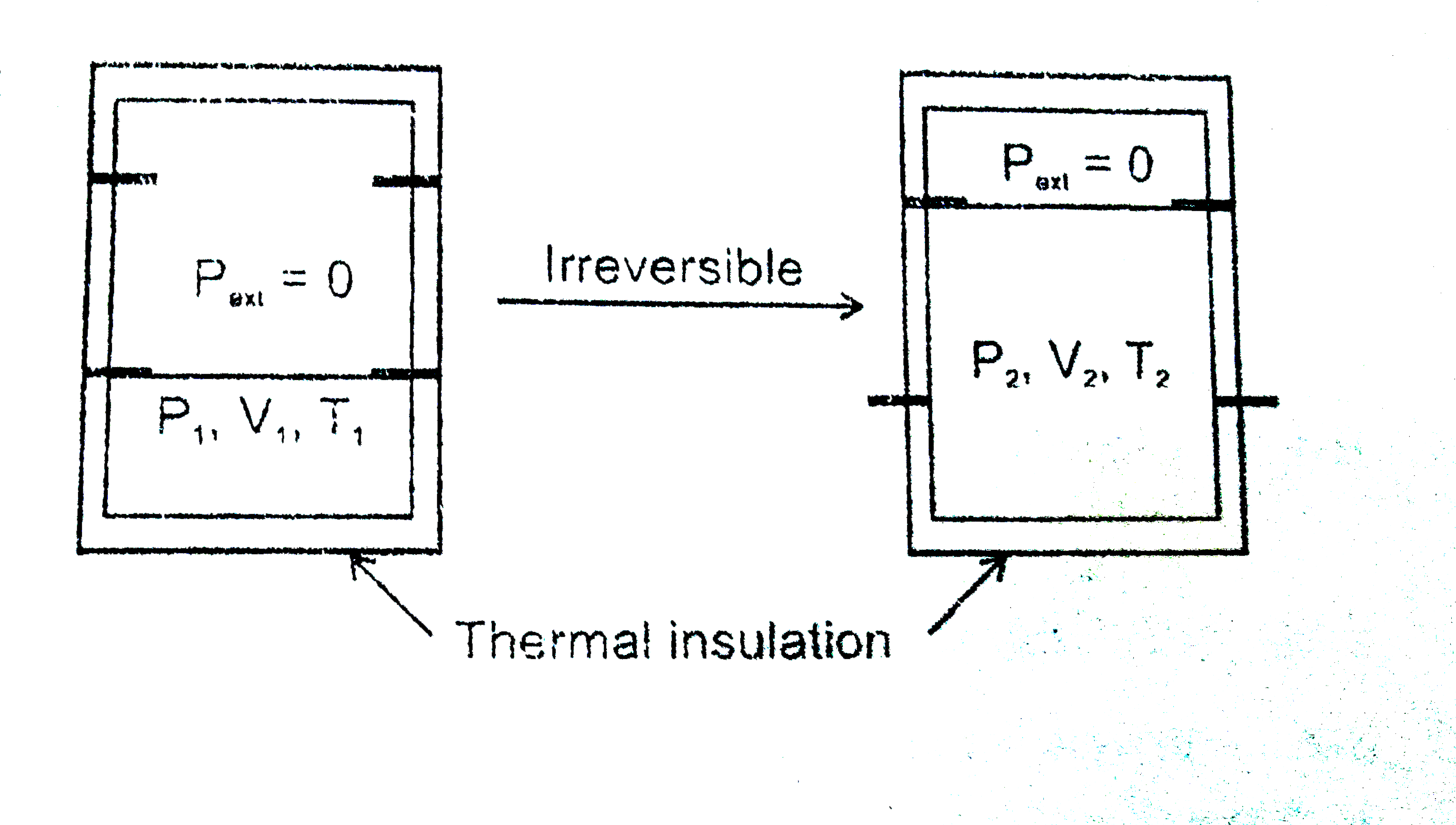
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure = P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2andT2, respectively. For this expansion.
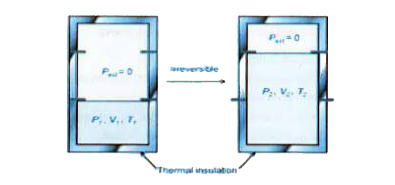
View Solution
