Two thin glass plates are placed parallel to each other such that distance between them is very small. Each glass plate reflects 25% of incident energy and transmits remaining 75% Light beam is incident on this system. Consider the interference of two light beams obtained after one reflection from each glass plate. Calculate ratio of the maximum to minimum intensity.
To solve the problem, we need to calculate the ratio of maximum to minimum intensity of light after interference from two thin glass plates. Here’s a step-by-step breakdown of the solution:
Step 1: Define the Incident Intensity
Let the intensity of the incident light beam be I.
Step 2: Calculate Reflected and Transmitted Intensities
- Reflection from the first plate: The first plate reflects 25% of the incident intensity, so the reflected intensity I1 is:
I1=25100I=I4
- Transmission through the first plate: The transmitted intensity It (which goes to the second plate) is:
It=75100I=3I4
Step 3: Calculate the Intensities After Reflection from the Second Plate
- Reflection from the second plate: The intensity that is reflected from the second plate (after transmission through the first plate) is:
I2=25100(3I4)=3I16
Step 4: Calculate the Intensities for Interference
Now we have two light beams:
- I1=I4 (from the first plate)
- I2=3I16 (from the second plate)
Step 5: Calculate Maximum Intensity
The maximum intensity Imax when the two beams interfere constructively is given by:
Imax=(√I1+√I2)2
Calculating √I1 and √I2:
- √I1=√I4=√I2
- √I2=√3I16=√3I4
Now substituting into the formula:
Imax=(√I2+√3I4)2
Finding a common denominator:
=(2√I4+√3I4)2=((2+√3)√I4)2
=(2+√3)2I16
Calculating (2+√3)2:
=4+4√3+3=7+4√3
Thus,
Imax=(7+4√3)I16
Step 6: Calculate Minimum Intensity
The minimum intensity Imin when the two beams interfere destructively is given by:
Imin=∣∣√I1−√I2∣∣2
Substituting the values:
Imin=(√I2−√3I4)2
Finding a common denominator:
=(2√I4−√3I4)2=((2−√3)√I4)2
=(2−√3)2I16
Calculating (2−√3)2:
=4−4√3+3=7−4√3
Thus,
Imin=(7−4√3)I16
Step 7: Calculate the Ratio of Maximum to Minimum Intensity
Now we can find the ratio:
ImaxImin=(7+4√3)I16(7−4√3)I16=7+4√37−4√3
Final Step: Simplify the Ratio
To simplify:
=(7+4√3)(7+4√3)(7−4√3)(7+4√3)=(7+4√3)249−48=(7+4√3)2
Calculating (7+4√3)2:
=49+56√3+48=97+56√3
Thus, the final answer for the ratio of maximum to minimum intensity is:
Ratio=49
Let the intensity of the incident light beam be I.
- Reflection from the first plate: The first plate reflects 25% of the incident intensity, so the reflected intensity I1 is:
I1=25100I=I4
- Transmission through the first plate: The transmitted intensity It (which goes to the second plate) is:
It=75100I=3I4
- Reflection from the second plate: The intensity that is reflected from the second plate (after transmission through the first plate) is:
I2=25100(3I4)=3I16
Now we have two light beams:
- I1=I4 (from the first plate)
- I2=3I16 (from the second plate)
The maximum intensity Imax when the two beams interfere constructively is given by:
Imax=(√I1+√I2)2
Calculating √I1 and √I2:
- √I1=√I4=√I2
- √I2=√3I16=√3I4
Imax=(√I2+√3I4)2
Finding a common denominator:
=(2√I4+√3I4)2=((2+√3)√I4)2
=(2+√3)2I16
Calculating (2+√3)2:
=4+4√3+3=7+4√3
Thus,
Imax=(7+4√3)I16
The minimum intensity Imin when the two beams interfere destructively is given by:
Imin=∣∣√I1−√I2∣∣2
Substituting the values:
Imin=(√I2−√3I4)2
Finding a common denominator:
=(2√I4−√3I4)2=((2−√3)√I4)2
=(2−√3)2I16
Calculating (2−√3)2:
=4−4√3+3=7−4√3
Thus,
Imin=(7−4√3)I16
Now we can find the ratio:
ImaxImin=(7+4√3)I16(7−4√3)I16=7+4√37−4√3
To simplify:
=(7+4√3)(7+4√3)(7−4√3)(7+4√3)=(7+4√3)249−48=(7+4√3)2
Calculating (7+4√3)2:
=49+56√3+48=97+56√3
Ratio=49
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - NCERT FILE SOLVED (TEXT BOOK EXERCISES)10videos
WAVE OPTICAL
- BOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - NCERT FILE SOLVED (Additional Exercises)11videos
WAVE OPTICAL
- BOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - Conceptual Questions23videos
WAVE OPTICAL
- BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION12videos
SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS
Similar Questions
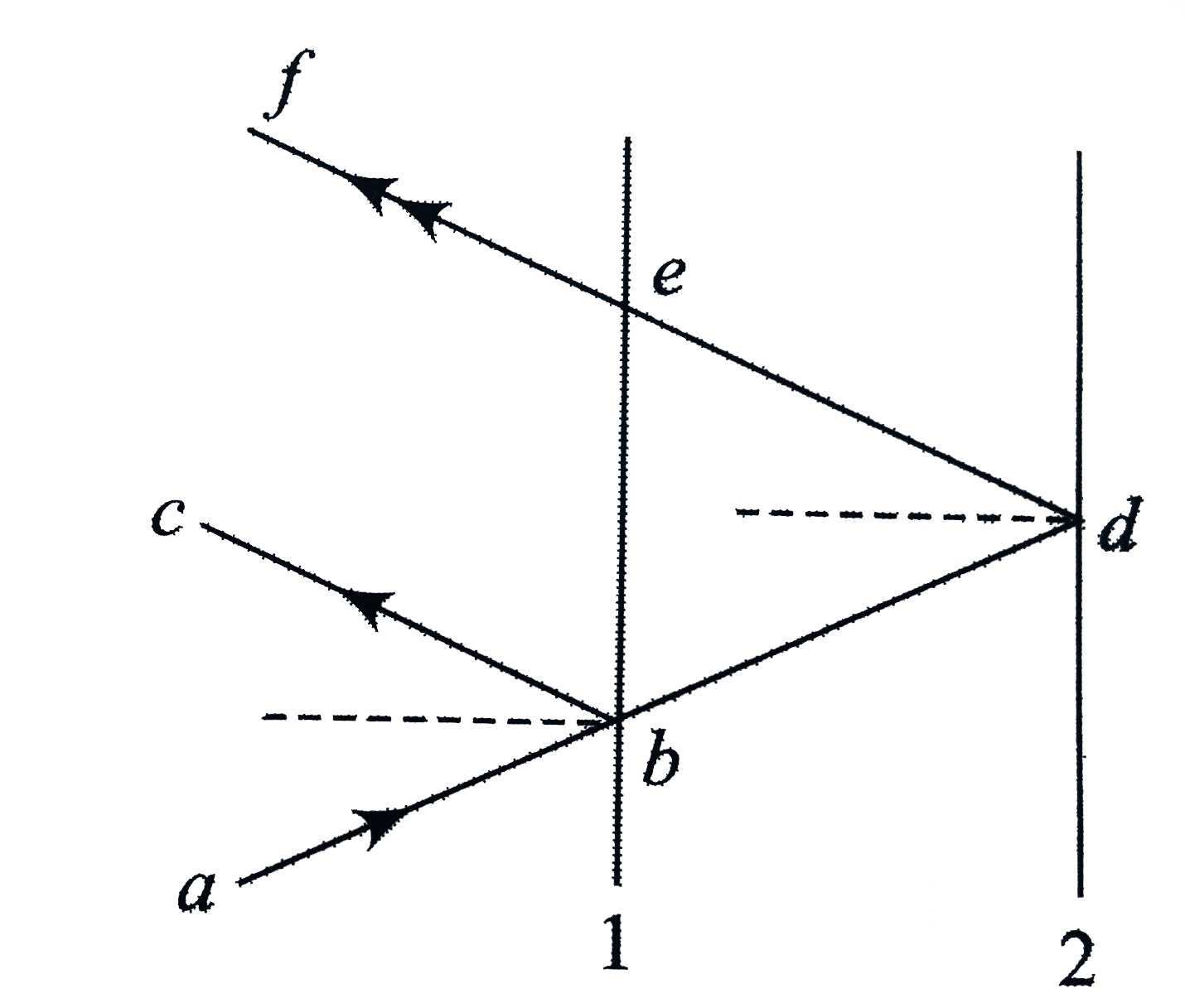
_E01_107_Q01.png)
A narrow monochromatic beam of light of intensity I is incident on a galss plate as shown in figure. Another identical glass plate is kept close to the first one & parallel to it. Each glass plate reflects 25% of the light incident on it % transmits the remaining find the ratio of the minimum & the maximum intensities in the interference pattern formed by the two beams obtained after one reflection at each plate.View SolutionA narrow monochromatic beam of light of intensity I is incident on a glass plate. Another identical glass plate is kept close to the first one and parallel to it. Each plate reflects 25% of the incident light and transmits the remaining. Calculate the ratio of minimum and maximum intensity in the interference pattern fromed by two beams obtained after reflection from each plate.
View Solution
Knowledge Check
- Question 1 - Select One
Two polaroids are kept crossed to each other . If one of them is rotated an angle 60∘ , the percentage of incident light now transmitted through the system is
A10%B20%C25%D12.5% - Question 2 - Select One
A parallel beam of light of intensity I is incident on a glass plate. 25% of light is reflected in any reflection by upper surface and 50% of light is reflected by any reflection from lower surface. Rest is refracted The ratio of maximum to minimum intensity in interference region of reflected rays is
 A⎛⎜ ⎜⎝12+√3812−√38⎞⎟ ⎟⎠2B⎛⎜ ⎜⎝14+√3812−√38⎞⎟ ⎟⎠2C58DNone of these
A⎛⎜ ⎜⎝12+√3812−√38⎞⎟ ⎟⎠2B⎛⎜ ⎜⎝14+√3812−√38⎞⎟ ⎟⎠2C58DNone of these - Question 3 - Select One
Two polaroids are kept crossed to each other. Now one of them is rotated through an angle of 45∘ . The percentage of incident light now transmitted through the system is
A15%B25%C50%D60%
A narrow monochromatic beam of light of intensity 1 is incident on a glass plate as shown in figure Another identical glass plate is kept close to the first one and parallel to it. Each glass plate reflects 25% of the light incident on it and transmits intensities in the interference pattern formed by two beams obtained after one reflection at each plate.
 View Solution
View SolutionTwo large glass plates are placed vertically and parallel to each other inside a tank of water with separation between the plates equal to 1 mm. Find the rise of water in the space between the plates. Surface tension of water =0.075Nm−1.
View SolutionTwo polaroids are placed such that their planes are parallel to each other with their access of transmission at 30°. If an unpolarised light of intensity I0 is incident on first polaroid polarizer then intensity of light that will be transmitted through the second polaroid is
View SolutionA ray of light is incident on the left vertical face of the glass slab. If the incident light has an intensity I and on each reflection the intensity decreases by 90% and on each refraction the intensity decreases by 10%, find the ratio of the intensities of maximum to minimum in reflected pattern.
 View Solution
View SolutionA ray of light in incident on a glass plate at an angle of 60∘. What is the refractive index of glass if the reflected and refracted rays are perpendicular to each other?
View Solution

