Two walls of thickness in the ratio 1:3 and thermal conductivities in the ratio 3:2 form a composite wall of a building. If the free surfaces of the wall be at temperatures 30∘C and 20∘C, respectively, what is the temperature of the interface?
To solve the problem, we will follow these steps:
Step 1: Define the Parameters
Let:
- Thickness of wall 1 = L
- Thickness of wall 2 = 3L
- Thermal conductivity of wall 1 = 3k
- Thermal conductivity of wall 2 = 2k
Step 2: Set Up the Temperature Conditions
- Temperature at the free surface of wall 1 = T1=30∘C
- Temperature at the free surface of wall 2 = T2=20∘C
- Let the temperature at the interface be T.
Step 3: Write the Heat Current Equations
Since the walls are in series, the heat current through both walls is equal:
H1=H2
For wall 1:
The heat current H1 can be expressed as:
H1=T1−TR1
Where R1 is the thermal resistance of wall 1:
R1=L3k
Thus,
H1=30−TL3k=3k(30−T)L
For wall 2:
The heat current H2 can be expressed as:
H2=T−T2R2
Where R2 is the thermal resistance of wall 2:
R2=3L2k
Thus,
H2=T−203L2k=2k(T−20)3L
Step 4: Set the Heat Currents Equal
Now, equate H1 and H2:
3k(30−T)L=2k(T−20)3L
Step 5: Simplify the Equation
Cancel k and L from both sides:
3(30−T)=23(T−20)
Step 6: Clear the Fraction
Multiply both sides by 3 to eliminate the fraction:
9(30−T)=2(T−20)
Step 7: Expand and Rearrange
Expanding both sides gives:
270−9T=2T−40
Rearranging the equation:
270+40=2T+9T
310=11T
Step 8: Solve for T
Now, divide both sides by 11:
T=31011≈28.18∘C
Final Answer
The temperature of the interface is approximately 28.18∘C.
---
Let:
- Thickness of wall 1 = L
- Thickness of wall 2 = 3L
- Thermal conductivity of wall 1 = 3k
- Thermal conductivity of wall 2 = 2k
- Temperature at the free surface of wall 1 = T1=30∘C
- Temperature at the free surface of wall 2 = T2=20∘C
- Let the temperature at the interface be T.
Since the walls are in series, the heat current through both walls is equal:
H1=H2
The heat current H1 can be expressed as:
H1=T1−TR1
Where R1 is the thermal resistance of wall 1:
R1=L3k
Thus,
H1=30−TL3k=3k(30−T)L
The heat current H2 can be expressed as:
H2=T−T2R2
Where R2 is the thermal resistance of wall 2:
R2=3L2k
Thus,
H2=T−203L2k=2k(T−20)3L
Now, equate H1 and H2:
3k(30−T)L=2k(T−20)3L
Cancel k and L from both sides:
3(30−T)=23(T−20)
Multiply both sides by 3 to eliminate the fraction:
9(30−T)=2(T−20)
Expanding both sides gives:
270−9T=2T−40
Rearranging the equation:
270+40=2T+9T
310=11T
Now, divide both sides by 11:
T=31011≈28.18∘C
The temperature of the interface is approximately 28.18∘C.
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise 1.1
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise 1.2
22 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Three bars of equal lengths and equal area of cross-section are connected in series fig. their thermal conducitives are in the ratio 2:3:4. If at the steady state the open ends of the first and the last bars are at temperature 200∘C and 20∘C respectively, find the temperature of both the junctions.
 .
.
View SolutionThree bars of equal lengths and equal areas of cross-section are connected in series. Their thermal conductivities are in the ratio of 2:4:3. If the open ends of the first and last bars are at temperatures 20∘Cand18∘C respectively in the steady state calculate the temperature of both the junctions.
View Solution
Knowledge Check
The slab shown in the figure consists of two parallel layers of cooper anb brass of same thickness and having thermal conductivites in the ratio 4:1. IF the free face of the brass is at 100∘C and that of copper is at 0∘C, then the temperature of the interface will be
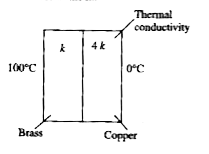 A20∘CB30∘CC40∘CD25∘C
A20∘CB30∘CC40∘CD25∘CTwo walls of thickness d1andd2 and thermal conductivites K1andK2 are in contact. In the steady state, if the temperature at the outer surfaces are T1andT2 the temperature at the common wall is
AK1T1d2+K2T2d1K1d2+K2d1BK1T1+K2T2d2+d1C(K1d1+K2d2T1+T2)T1T2DK1T1d1+K2T2d2K1d1+K2d2
Two plates of equal area are placed in contact with each other. The thickness of the plates are 2.0 cm and 3.0 cm respectively. The outer face of first plate is at −25∘C and that of second plate is at +25∘C. The conductivities of the plates are in the ratio 2:3. Calculate the temperature of the common surface of the plates.
View Solution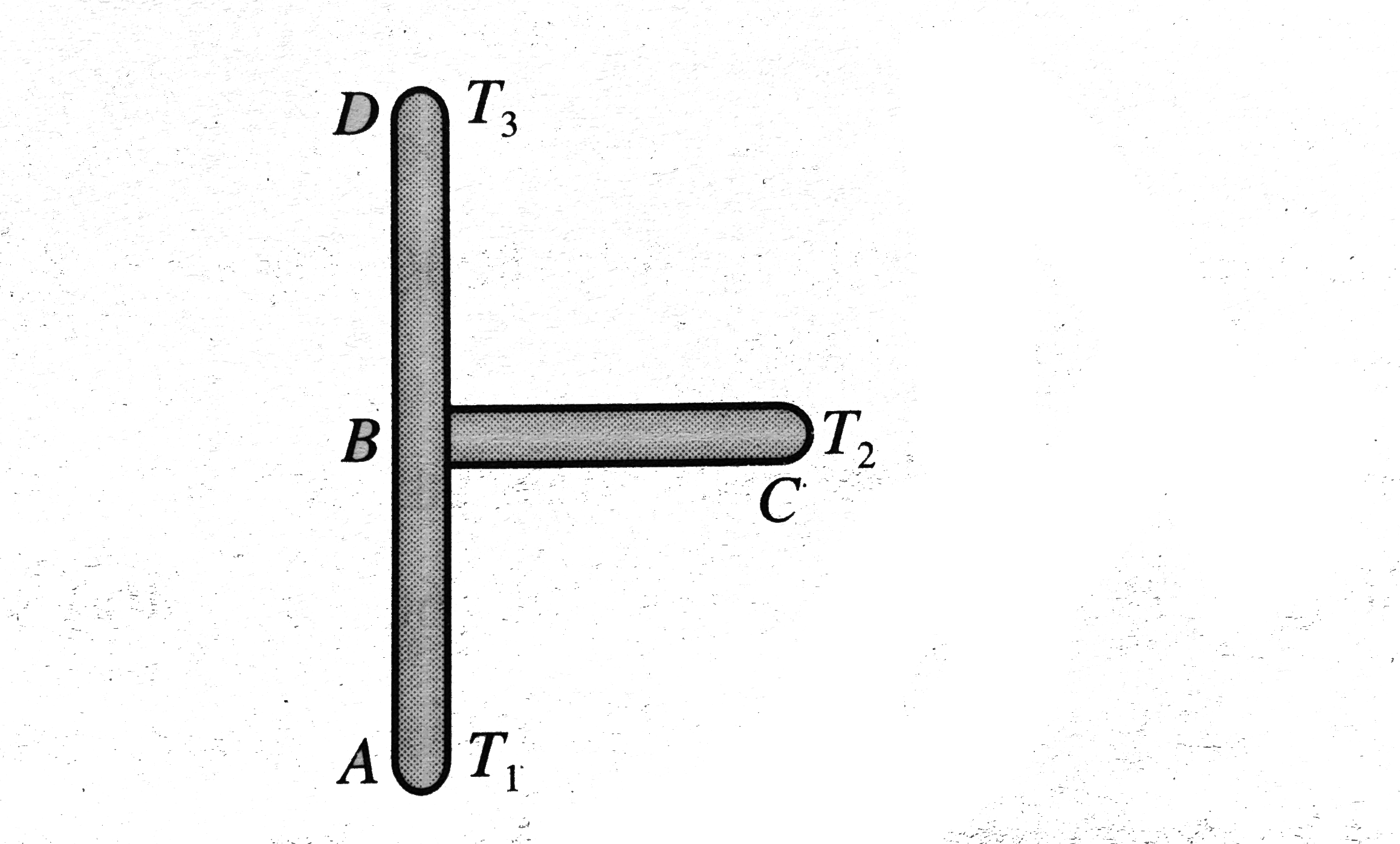
Three rods AB, BC and BD having thermal conductivities in the ratio 1:2:3 and lengths in the ratio 2:1:1 are joined as shown in Fig. The ends A, C and D are at temperature T1,T2 and T3 respectively Find the temperature of the junction B. Assume steady state.
View SolutionThree rods A, B and C of the same length and same cross-sectional area are joined as shown. Their thermal conductivities are in the ratio 1:2:3/2. If the open ends of A and C are at 200∘C and 18∘C, respectively, then the temperature at the junction of A at steady state is
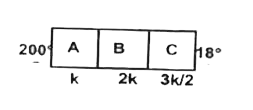
View SolutionIn the figure ABC is a conducting rod whose lateral surfaces are insulated. The length of the section AB is one-half of that of BC, and the respective thermal conductivities of the two sections are as given in the figure. If the ends A and C are maintained at 0∘C and 70∘C respectively, the temperature of junction B in the steady state is

View SolutionDensities of two gases are in the ratio 1:2 and their temperatures are in the ratio 2:1, then the ratio of their respective pressure is
View Solution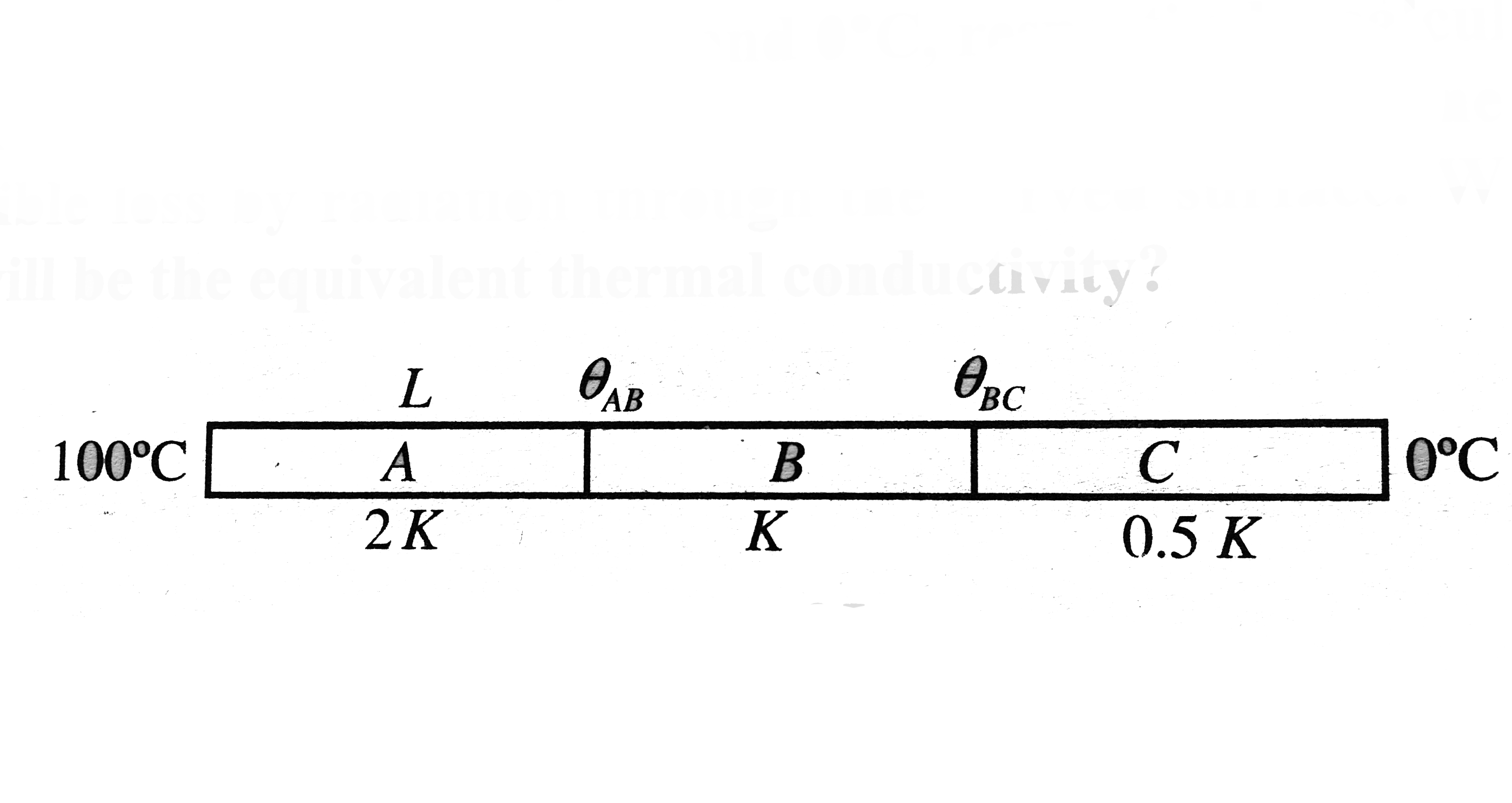
Three cylindrical rods A, B and C of equal lengths and equal diameters are joined in series as shown if Fig. Their thermal conductivities are 2K, K and 0.5K, respectively. In steady state, if the free ends of rods A and C are at 100∘C and 0∘C, respectively, calculate the temperature at the two junction points. Assume negligible loss by radiaiotn through the curved surface. What will be the equivalent thermal conductivity?
View Solution
