Two wires A and B are of lengths 40 cm and 30 cm. A is bent into a circle of radius r and B into an arc of radius r. A current i1 is passed through A and i2 through B. To have the same magnetic induction at the centre, the ratio of i1 : i2 is
3:4
3:5
2:3
4:3
The correct Answer is:A
To solve the problem, we need to find the ratio of currents i1 and i2 such that the magnetic induction at the center of wire A (bent into a circle) and wire B (bent into an arc) is the same.
1. Determine the Circumference of Wire A:
- The length of wire A is given as 40 cm. When bent into a circle, the circumference C is:
C=2πr=40 cm
- From this, we can find the radius r:
r=402π=20π cm
2. Magnetic Induction at the Center for Wire A:
- The formula for the magnetic induction B1 at the center of a circular loop carrying current i1 is given by:
B1=μ0i12r
3. Determine the Length of Wire B:
- The length of wire B is given as 30 cm. Since it is bent into an arc of radius r, we can express the angle θ in radians subtended by the arc:
θ⋅r=30 cm
- Substituting r from step 1:
θ⋅20π=30⟹θ=30π20=3π2 radians
4. Magnetic Induction at the Center for Wire B:
- The formula for the magnetic induction B2 at the center of an arc carrying current i2 is:
B2=μ0i2θ4πr
5. Set the Magnetic Inductions Equal:
- To have the same magnetic induction at the center, we set B1=B2:
μ0i12r=μ0i2θ4πr
- We can cancel μ0 and r from both sides:
i12=i2θ4π
6. Substitute for θ:
- Substitute θ=3π2:
i12=i2⋅3π24π
- Simplifying the right side:
i12=3i28
7. Solve for the Ratio i1i2:
- Cross-multiplying gives:
8i1=6i2⟹i1i2=68=34
Final Result:
The ratio of currents i1:i2 is:
i1i2=34
- The length of wire A is given as 40 cm. When bent into a circle, the circumference C is:
C=2πr=40 cm
- From this, we can find the radius r:
r=402π=20π cm
- The formula for the magnetic induction B1 at the center of a circular loop carrying current i1 is given by:
B1=μ0i12r
- The length of wire B is given as 30 cm. Since it is bent into an arc of radius r, we can express the angle θ in radians subtended by the arc:
θ⋅r=30 cm
- Substituting r from step 1:
θ⋅20π=30⟹θ=30π20=3π2 radians
- The formula for the magnetic induction B2 at the center of an arc carrying current i2 is:
B2=μ0i2θ4πr
- To have the same magnetic induction at the center, we set B1=B2:
μ0i12r=μ0i2θ4πr
- We can cancel μ0 and r from both sides:
i12=i2θ4π
- Substitute θ=3π2:
i12=i2⋅3π24π
- Simplifying the right side:
i12=3i28
- Cross-multiplying gives:
8i1=6i2⟹i1i2=68=34
The ratio of currents i1:i2 is:
i1i2=34
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-II
79 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
3 Videos
Similar Questions
A circular coil of average radius 6 cm has 20 turns. A current 1.0 A is set up through it. Find the magnetic induction at
(i) The centre of the coil
View SolutionTwo identical wires AandB , each of length 'l', carry the same current I. Wire A is bent into a circle of radius RandwireB is bent to form a square of side 'a' . If BAandBB are the values of magnetic field at the centres of the circle and square respectively , then the ratio BABB is :
View SolutionTwo identical wires AandB , each of length 'l', carry the same current I. Wire A is bent into a circle of radius RandwireB is bent to form a square of side 'a' . If BAandBB are the values of magnetic field at the centres of the circle and square respectively , then the ratio BABB is :
View SolutionIf a straight conductor of length 40cm bent in the form of a square and the current 2A is allowed to pass through square, then find the magnetic induction at the centre of the square loop
View SolutionAn infinitely long conductor is bent into a circle as shown in figure. It carries a current I ampere and the radius of loop is R metre. The magnetic induction at the centre of loop is
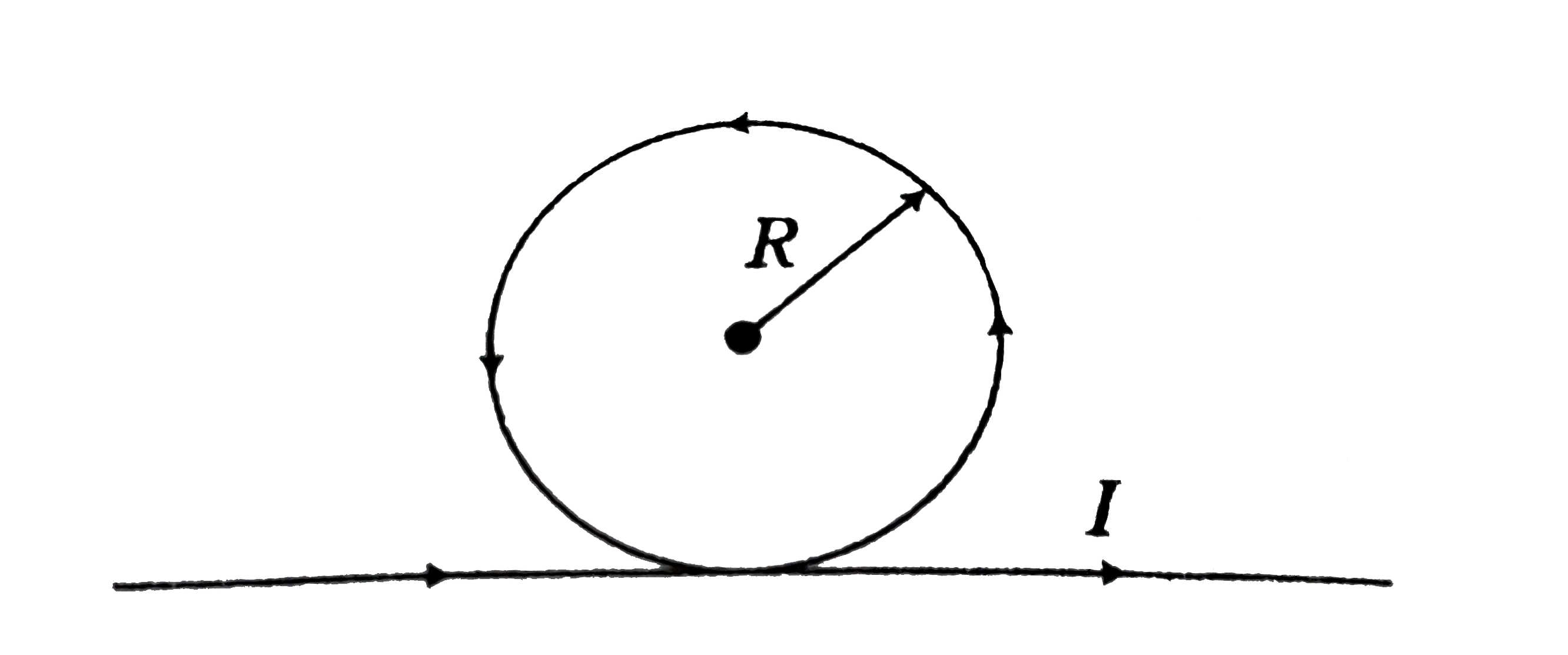
View SolutionA wire is bent in the form of a circular arc of radius r with a straight portion AB. If the current in the wire is i, then the magnetic induction at point O is

View SolutionCurrent I A flowing in a circular coil of radius r. then the magnetic induction at the centre is B. If the current is doubled then the magnetic induction will be
View SolutionTwo bars of radius r and 2r are kept in constant as shown in figure. An electric current I is passed through the bars. Which of the following is correct?

View SolutionA wire of certain length carries a current l.It is bent to form a circle of one turn and the magnetic field at the centre is B1. If it is bent to form a coil of four turns, then magnetic field at centre is B2.The ratio of B1 and B2is
View SolutionA current i ampere flows in a circular arc of wire whose radius is R, which subtend an angle 3π/2 radian at its centre. The magnetic induction B at the centre is

View Solution
