Two wires of equal length and cross -section area are suspended as shown in figure. Their Young's modulus are Y1andY2 respectively. The equivalent Young's modulus will be

Y1+Y2
Y1+Y22
Y1Y2Y1+Y2
√Y1Y2
The correct Answer is:B
Young.s modulus,
Y=FA×LΔL
Force constant of a wire is
k=FΔL=YAL
Refer figure, the equivalent force constant is keq=k1+k2
or Y(2A)L=Y1AL+Y2ALorY=Y1+Y22

Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Check Your Neet Vitals
22 Videos
- PROPERTIES OF BULK MATTERBOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - AIPMT/NEET (MCQs)
40 Videos
- PROPERTIES OF BULK MATTERBOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - AIPMT/NEET (MCQs)
40 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - MTG GUIDECHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - AIPMT / NEET MCQ
14 Videos
- THERMODYNAMICSBOOK - MTG GUIDECHAPTER - THERMODYNAMICSEXERCISE - AIPMT/NEET (MCQs)
26 Videos
Similar Questions
Two wires of equal length and cross-section area suspended as shown in figure. Their Young's modulus are Y1 and Y2 respectively. The equavalent Young's modulus will be

View SolutionTwo wires of equal length and cross-sectional area are suspended as shown in figure. Their Young's modullare Y1 andY2 respectively. The equivalent Young's modulil will bebr>
View Solution
Knowledge Check
Two wires of equal length and cross-section area suspended as shown in figure. Their Young's modulus are Y1 and Y2 respectively. The equavalent Young's modulus will be
 AY1+Y2BY1−Y22CY1Y2Y1+Y2D√Y1Y2
AY1+Y2BY1−Y22CY1Y2Y1+Y2D√Y1Y2Three vertical wires, I,II and III are supporting a block of mass M in horizontal positon. The wires are to equal length and cross-sectional area. It is given that Young's modulus of wire II,Y2=Y3 (Yong's modulus of wire III). The wire I and III and attached at extreme ends of the block.
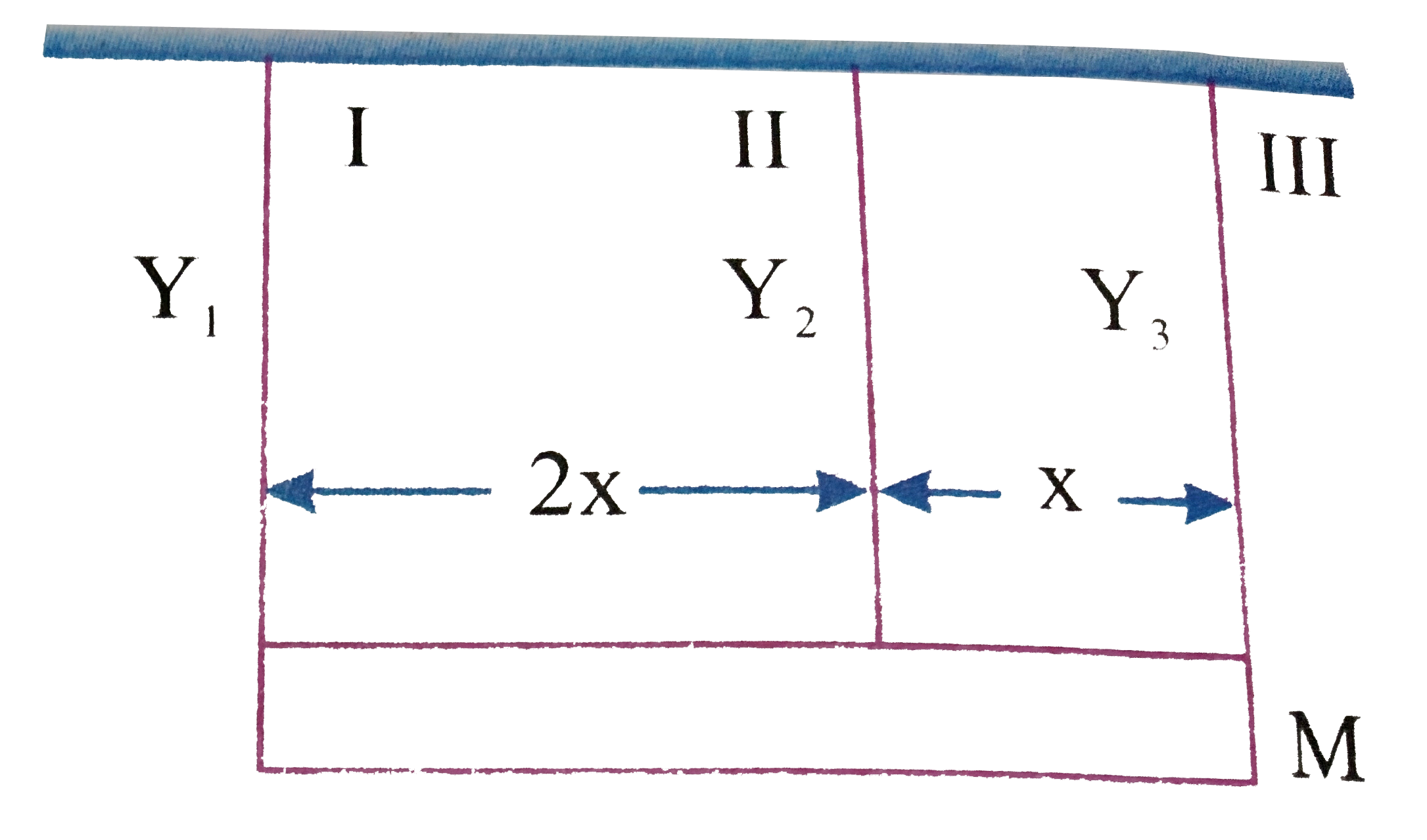 AT1=2T3B2T1=T3CT2=T3DT1=Mg/5
AT1=2T3B2T1=T3CT2=T3DT1=Mg/5
Two wires of equal length and cross sectional area suspended as shown in
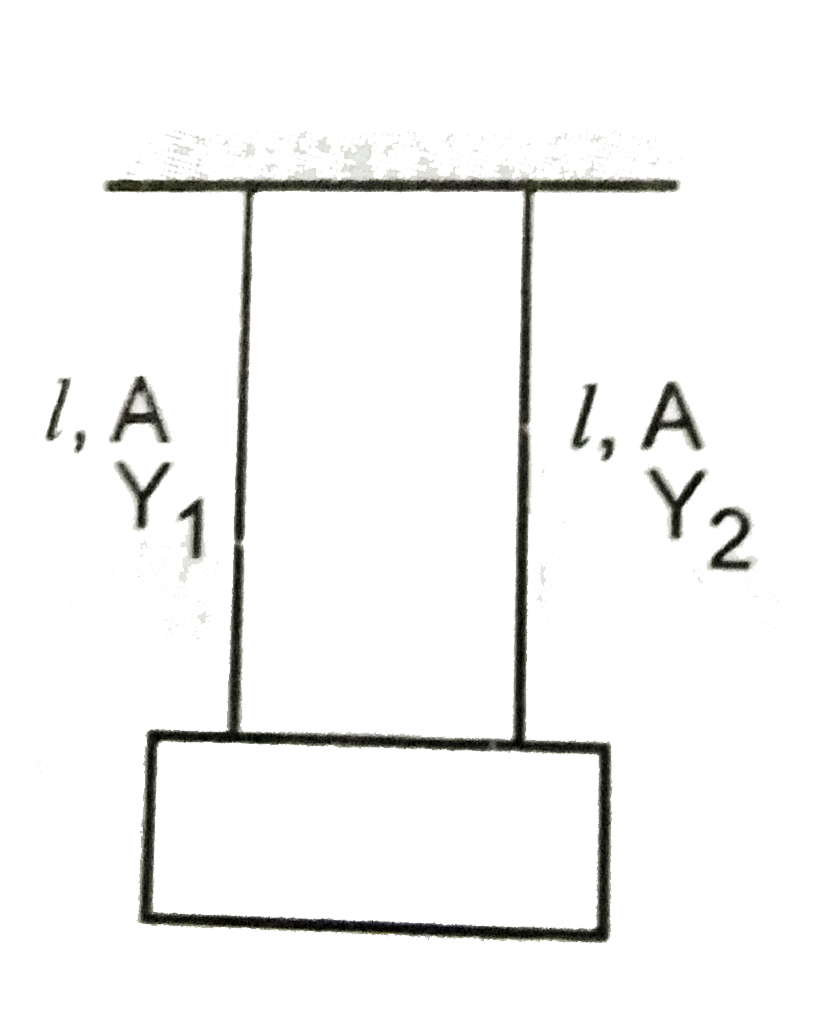
Their Young's modulii are Y1=2×1011 Pa and Y2=0.90×1011 Pa respectively. What will be the equivalent Young's modulus of combination?
View SolutionTwo wires of equal length and cross sectional area suspended as shown in

Their Young's modulii are Y1=2×1011 Pa and Y2=0.90×1011 Pa respectively. What will be the equivalent Young's modulus of combination?
View SolutionTwo wires of equal length and cross sectional area suspended as shown in

Their Young's modulii are Y1=2×1011 Pa and Y2=0.90×1011 Pa respectively. What will be the equivalent Young's modulus of combination?
View SolutionA horizontal rod suspended from two wires of same length and cross - section. Their Young's modulus are Y1 and Y2 respectively. The equivalent Young's modulus will be

View SolutionTwo wires have identical lengths and areas of cross-section are suspended by mass M. Their Young's modulus are in the ratio 2:5.
View SolutionTwo wires have identical lengths and areas of cross-section are suspended by mass M. Their Young's modulus are in the ratio 2:5.
View Solution
