Velocity-time equation of a particle moving in a straight line is, v=(10+2t+3t2) (SI units) Find
(a) displacement of particle from the mean position at time t=1s, if it is given that displacement is 20m at time t=0.
(b) acceleration-time equation.
The correct Answer is:A
(a) The given equation can be written as,
v=dsdt=(10+2t+3t2)ords=(10+2t+3t2)dt
or ∫s20ds=∫10(10+2t+3t2)dt or s−20=[10t+t2+t3]10
or s=20+12=32m
(b) Acceleration-time equation can be obtained by differentiating the given equation w.r.t. time.
Thus, a=dvdt=ddt(10+2t+3t2) or a=2+6t
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Example Type 1
1 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Example Type 2
1 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
Velocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. Plot the corresponding displacement-time graph of the particle if at time t=0, displacement s=0.
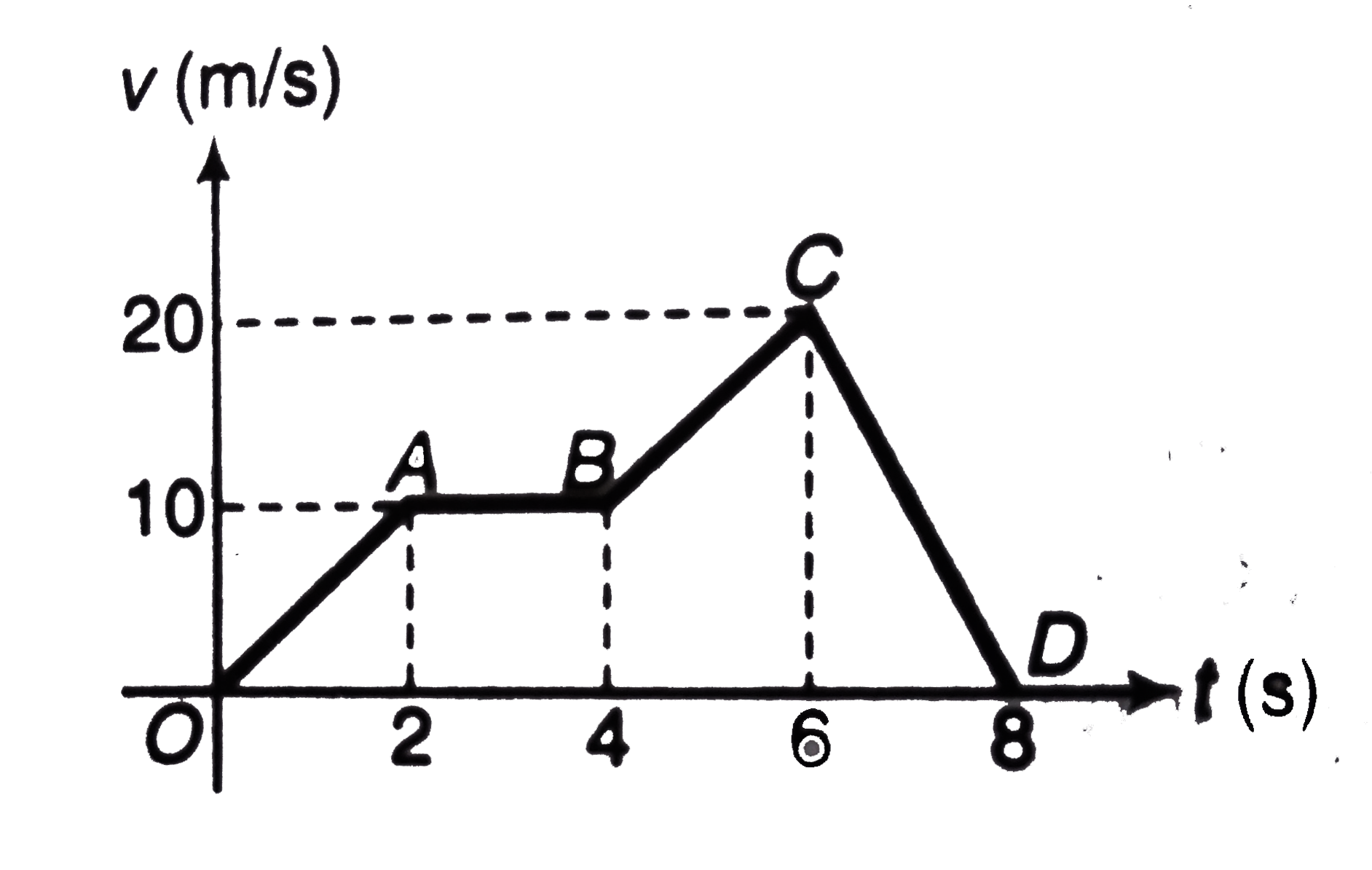
View Solution
Knowledge Check
Velocity time equation of a particle moving in a straight line is v=2t−4 for t≤2s and v=4−2t for t>2.The distance travelled by the particle in the time interval from t=0 to t=4s is (Here t is in second and v in m/s)
A12mB16mC4mD8mThe velocity -time (v−t) graph of a particle moving in a straight line is shown in figure. The acceleration of the particle at t=9 is:
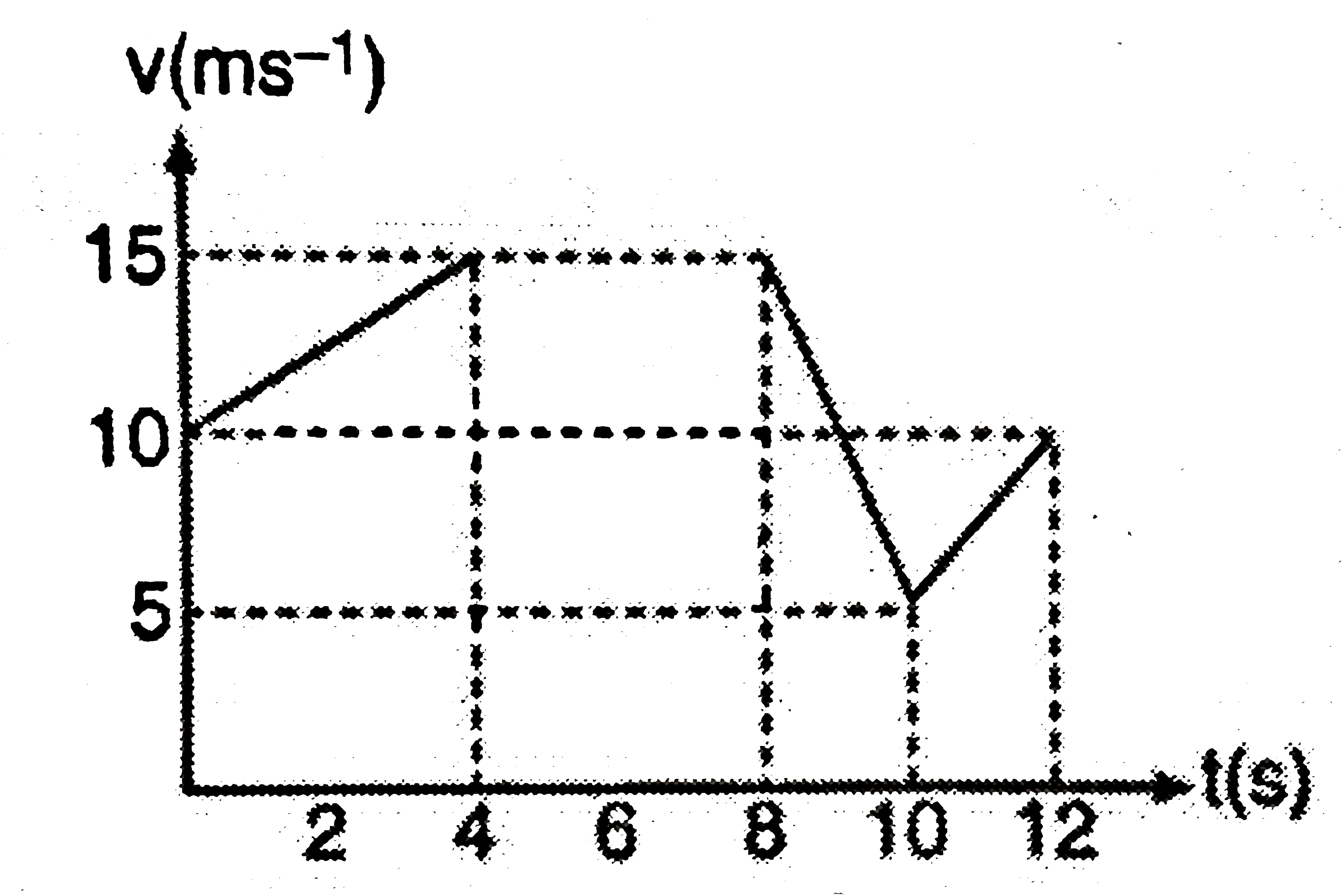 AzeroB5ms−2C−5ms2D−2ms−2
AzeroB5ms−2C−5ms2D−2ms−2For a particle moving in a straight line assume s,v,a and t represents displacement, velocity, acceleration and time respectively.
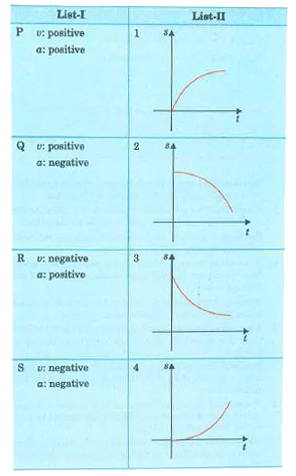 APQRS3241BPQRS1324CPQRS2134DPQRS4132
APQRS3241BPQRS1324CPQRS2134DPQRS4132
Velocity-time graph of a particle moving in a straight line is shown in figure. At time t=0, displacement of the particle from mean position is 10 m. Find
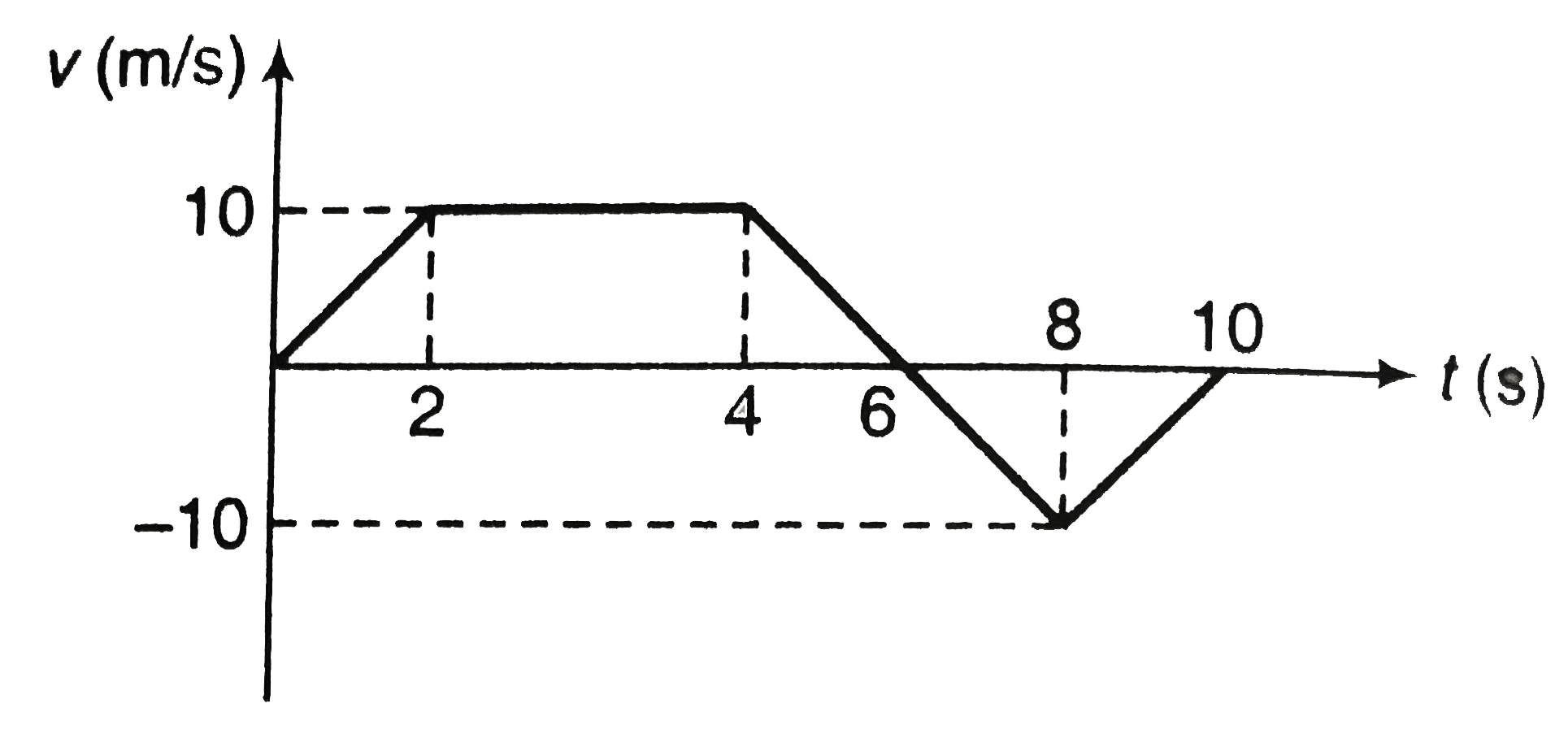
(a) acceleration of particle at t=1s,3sand9s.
(b) position of particle from mean position at t=10s.
(c) write down s-t equation for time interval (i)0≤t≤2s, (ii) 4s≤t≤8s
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. At time t=0.s=20m. Plot a-t and s-t graphs of the particle.
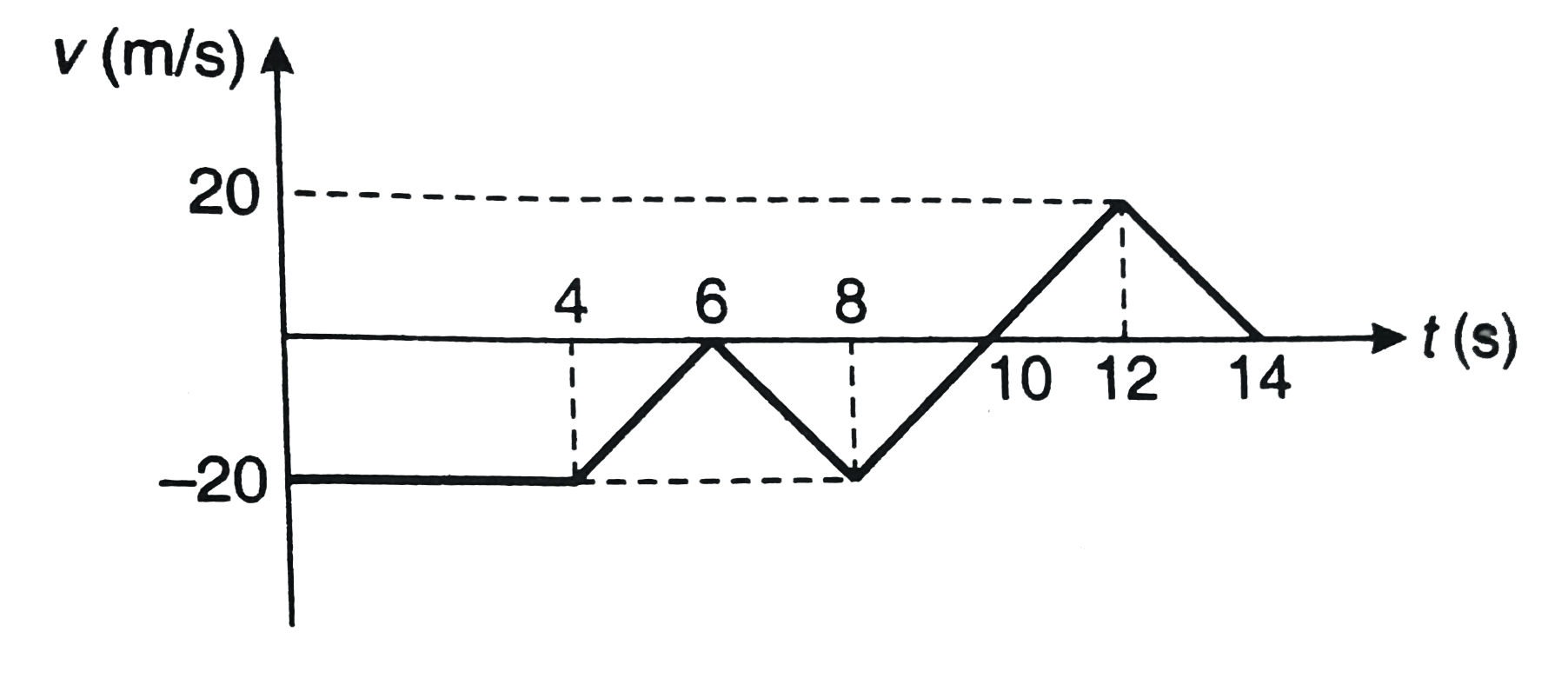
View SolutionVelocity (in m/s) of a particle moving along x-axis varies with time as, v=(10+5t−t2) At time t=0,x=0. Find
(a) acceleration of particle at t=2s and
(b) x-coordinate of particle at t=3s
View SolutionVelocity of a particle at any time t is v=(2ˆi+2tˆj)m/s. Find acceleration and displacement of particle at t=1s. Can we apply v=u+at or not?
View SolutionA particle is moving in a straight line according to graph given below : (a is acceleration, v is velocity, x is position, t is time) :
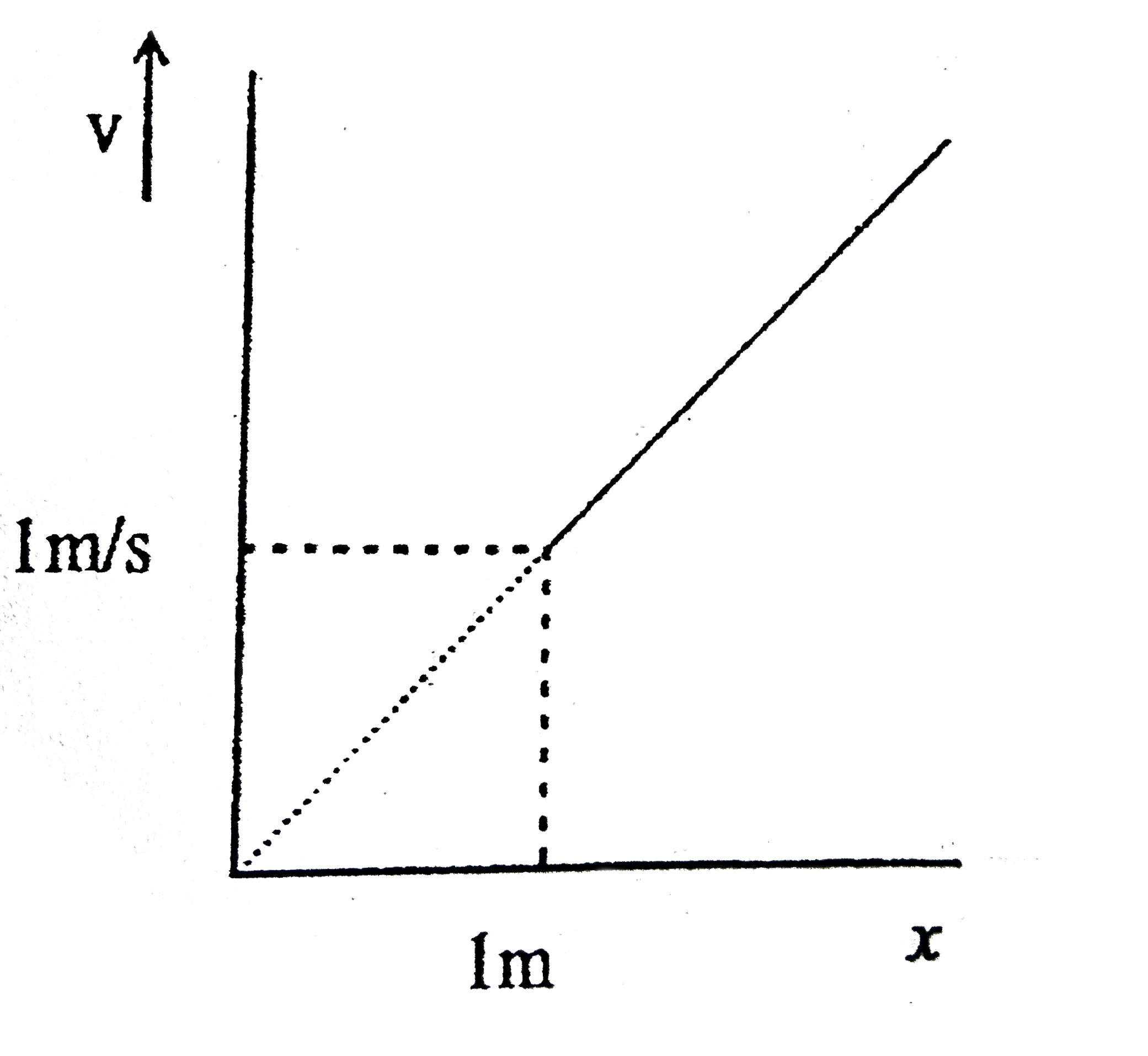
View Solution
