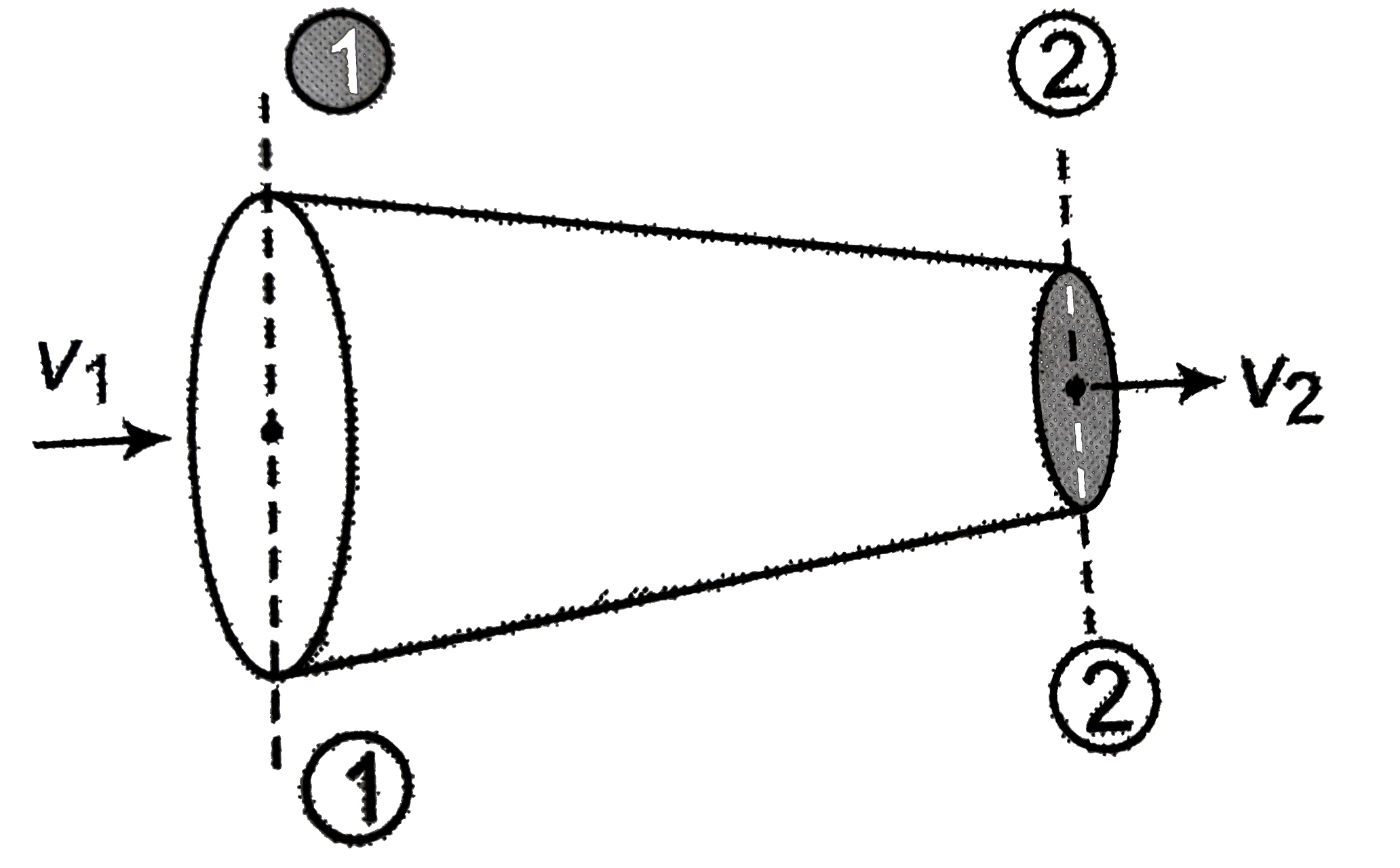
Water is flowing through a horizontal pipe of varying cross-section. If the pressure of water equals 2 cm of Hg where velocity of flow is $32 c m s^{- 1}$ , what is the pressure at another point where the velocity of flow is $40 c m s^{- 1}$ ?

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we will apply Bernoulli's principle, which states that for an incompressible, frictionless fluid, the total mechanical energy along a streamline is constant. The equation can be expressed as:
$P + \frac{1}{2} ρ V^{2} + ρ g h = constant$
Since the pipe is horizontal, the height (h) remains constant, and we can ignore the potential energy term ( $ρ g h$ ). Therefore, the equation simplifies to:
$P_{1} + \frac{1}{2} ρ V_{1}^{2} = P_{2} + \frac{1}{2} ρ V_{2}^{2}$
Step 1: Identify the known values
- $P_{1} = 2 cm of Hg$
- $V_{1} = 32 cm/s$
- $V_{2} = 40 cm/s$
Step 2: Convert pressure from cm of Hg to a consistent unit
The density of mercury ( $ρ_{H g}$ ) is $13.6 {g/cm}^{3}$ . We will convert the pressure into dynes/cm² for consistency:
$P_{1} = 2 cm of Hg = 2 \times 13.6 \times 980 {dynes/cm}^{2}$
Step 3: Substitute known values into Bernoulli's equation
Using the simplified Bernoulli's equation:
$P_{1} + \frac{1}{2} ρ V_{1}^{2} = P_{2} + \frac{1}{2} ρ V_{2}^{2}$
Rearranging for $P_{2}$ :
$P_{2} = P_{1} + \frac{1}{2} ρ V_{1}^{2} - \frac{1}{2} ρ V_{2}^{2}$
Step 4: Substitute the values into the equation
Substituting $P_{1}$ and the velocities:
$P_{2} = 2 \times 13.6 \times 980 + \frac{1}{2} ρ (32^{2}) - \frac{1}{2} ρ (40^{2})$
Step 5: Calculate the kinetic energy terms
The density of water ( $ρ$ ) is $1 {g/cm}^{3}$ , so:
$\frac{1}{2} ρ (32^{2}) = \frac{1}{2} \times 1 \times 1024 = 512 {dynes/cm}^{2}$
$\frac{1}{2} ρ (40^{2}) = \frac{1}{2} \times 1 \times 1600 = 800 {dynes/cm}^{2}$
Step 6: Substitute kinetic energy terms back into the equation
Now substituting these values back:
$P_{2} = 2 \times 13.6 \times 980 + 512 - 800$
Step 7: Calculate $P_{2}$
Calculating the pressure:
1. Calculate $2 \times 13.6 \times 980$ :
$2 \times 13.6 \times 980 = 26656 {dynes/cm}^{2}$
2. Now substitute:
$P_{2} = 26656 + 512 - 800$
$P_{2} = 26656 - 288$
$P_{2} = 26368 {dynes/cm}^{2}$
Step 8: Convert $P_{2}$ back to cm of Hg
To convert back to cm of Hg:
$P_{2} in cm of Hg = \frac{26368}{13.6 \times 980}$
Calculating:
1. Calculate $13.6 \times 980 = 13328$
2. Now divide:
$P_{2} = \frac{26368}{13328} \approx 1.978 cm of Hg$
Final Answer
Thus, the pressure at the point where the velocity of flow is $40 cm/s$ is approximately:
$P_{2} \approx 1.978 cm of Hg$
---

Updated on:7/8/2024

Water flows steadily through a horizontal pipe of a variable cross-section. If the pressure of water is p at a point where the velocity of flow is v, what is the pressure at another point where the velocity of flow is 2v, $ρ$ being the density of water?
A $p + 2 ρ v^{2}$
B $p - 2 ρ v^{2}$
C $p + \frac{3}{2} ρ v^{2}$
D $p - \frac{3}{2} ρ v^{2}$
Water flows steadily through a horizontal pipe of a variable cross-section. If the pressure of the water is p at a point , where the speed of the flow is v. What is the pressure at another point , where the speed of the flow is 2 v ? Let the density of water be $1 g c m^{- 3}$ .
A $p + (\frac{3}{2}) ρ v^{2}$
B $p - 2 ρ v^{2}$
C $p - 3 ρ v^{2}$
D $p - (\frac{3}{2}) ρ v^{2}$
Water flows steadily through a horizontal pipe of variable cross-section. If the pressure of water is $p$ at a point where the velocity of flow is $v$ , at another point (pressure $p'$ ), where the velocity of flow in $η v$ : The following statements are given below
A $\frac{p'}{p} < 1$ , when $η < 1$
B $\frac{p'}{p} < 1$ , when $η > 1$
C $\frac{p'}{p} > 1$ , when $η < 1$
D $\frac{p'}{p} > 1$ , when $η > 1$