What is the height to which a liquid rises between two long parallel plates, a distance d apart ? (Surface tension of liquid is T and density is )
The correct Answer is:B
To solve the problem of finding the height to which a liquid rises between two long parallel plates a distance d apart, we can follow these steps:
1. Understand the Setup:
- We have two long parallel plates separated by a distance d.
- The liquid rises to a height h between these plates due to surface tension.
2. Identify the Forces:
- The upward force due to surface tension acts along the perimeter of the liquid surface in contact with the plates.
- The downward force is due to the weight of the liquid column that has risen.
3. Calculate the Upward Force:
- The force due to surface tension FT can be expressed as:
FT=2T⋅L
where T is the surface tension and L is the length of the plates.
4. Calculate the Downward Force:
- The weight of the liquid column can be expressed as:
FW=Volume⋅Density⋅g=h⋅d⋅L⋅ρ⋅g
where ρ is the density of the liquid and g is the acceleration due to gravity.
5. Set Up the Equation:
- At equilibrium, the upward force due to surface tension equals the downward force due to the weight of the liquid:
2T⋅L=h⋅d⋅L⋅ρ⋅g
6. Simplify the Equation:
- We can cancel L from both sides (assuming L≠0):
2T=h⋅d⋅ρ⋅g
7. Solve for Height h:
- Rearranging the equation gives:
h=2Tρgd
Final Answer:
The height to which the liquid rises between the two plates is given by:
h=2Tρgd
- We have two long parallel plates separated by a distance d.
- The liquid rises to a height h between these plates due to surface tension.
- The upward force due to surface tension acts along the perimeter of the liquid surface in contact with the plates.
- The downward force is due to the weight of the liquid column that has risen.
- The force due to surface tension FT can be expressed as:
FT=2T⋅L
where T is the surface tension and L is the length of the plates.
- The weight of the liquid column can be expressed as:
FW=Volume⋅Density⋅g=h⋅d⋅L⋅ρ⋅g
where ρ is the density of the liquid and g is the acceleration due to gravity.
- At equilibrium, the upward force due to surface tension equals the downward force due to the weight of the liquid:
2T⋅L=h⋅d⋅L⋅ρ⋅g
- We can cancel L from both sides (assuming L≠0):
2T=h⋅d⋅ρ⋅g
- Rearranging the equation gives:
h=2Tρgd
The height to which the liquid rises between the two plates is given by:
h=2Tρgd
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Comprehension
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
Derive an expression for the height of capillary rise between two parrallel plates dipping in a liquid of density σ separated by a distance d. The surface tension of the liquid is T.
View SolutionWhat is the effect of temperature on the surface tension of a liquid ?
View SolutionIt is said that a liquid rises or is depressed in a capillary due to the surface tension. If a liquid neither rises nor depresses in a capillary, can we conclude that the surface tension of the liquid is zero ?
View SolutionWhich of the following does not affect surface tension of liquid?
View SolutionTwo parallel glass plates are dipped partly in the liquid of density 'd' keeping them vertical. If the distance between the plates is 'x', Surface tension is T and angle of contact is θ then rise of liquid between the plates due to capillary will be
View SolutionWhen a long capillary tube of radius 0.015 cm is dipped in a liquid, the liquid rises to a height of 15 cm within it. If the contact angle between the liquid and glass to close to 0∘, the surface tension of the liquid, in milliNewton m−1, is [ρliquid=900kgm−3,g=10ms−2] (give anwer is closet integer)
View SolutionA long wire of negligible thickness and mass per unit length λ is floating in a liquid such that the top surface of liquid dips by a distance 'y' If the lendth of base of vessel is 2a , find surface tension of the liquid (y>>a)
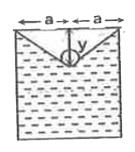
View SolutionA liquid of diameter D breaks up into 64 tiny drops. If the surface tension of the liquid is σ what is the change in energy?
View SolutionSurface tension of a liquid is a molecular phenomenon of liquids involving the force of cohesion along the liquid molecules. It is scalar quantity and is numberically equal to the surface energy. Numerically, it is proved that the potential soluble salts and surface active substance. Sparingly soluble salts and surface active substances decrease the surface tension of the liquid. However, the fairly soluble solutes increase the surface tension of the liquid. Surface tension of a liquid is independent of surface area but it depends on the intermolecular forces and the temperature.
Which among the following is not the unit of surface tension ?
View SolutionSurface tension of a liquid is a molecular phenomenon of liquids involving the force of cohesion along the liquid molecules. It is scalar quantity and is numerically equal to the surface energy. Numerically, it is proved that the potential soluble salts and surface active substance. Sparingly soluble salts and surface active substances decrease the surface tension of the liquid. However, the fairly soluble solutes increase the surface tension of the liquid. Surface tension of a liquid is independent of surface area but it depends on the intermolecular forces and the temperature.
Which of the following has the highest surface tension ?
View Solution
