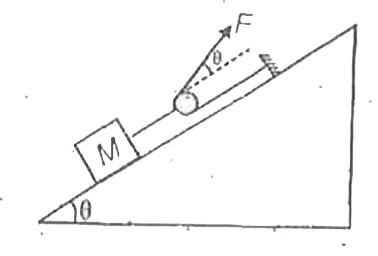
What should be the minimum force P to be applied to the string so that block of mass m just begins to move up the frictionless plane?

From force diagram of pulley.
P+Pcosθ=T
From force diagram of block
T>mgsinθ
or P+Pcosθ>mgsinθ
or P>mgsinθ1+cosθ
∴Pmin=mgsinθ1+cosθ

Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.3
19 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.4
13 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
Knowledge Check
An inclined plane is inclined at an angle θ with the horizontal. A body of mass m rests on it, if the coefficient of friction is μ, then the minimum force that has to be applied to the inclined plane to make the body just move up the inclined plane is
AmgsinθBμmgcosθCμmgcosθ−mgsinθDμmgcosθ+mgsinθFigure shown a block of mass m placed on a smooth wedge of mass M. Calculate the minimum value of M' and tension in the string, so that the block of mass m will move vertically downwards with acceleration 10ms−2
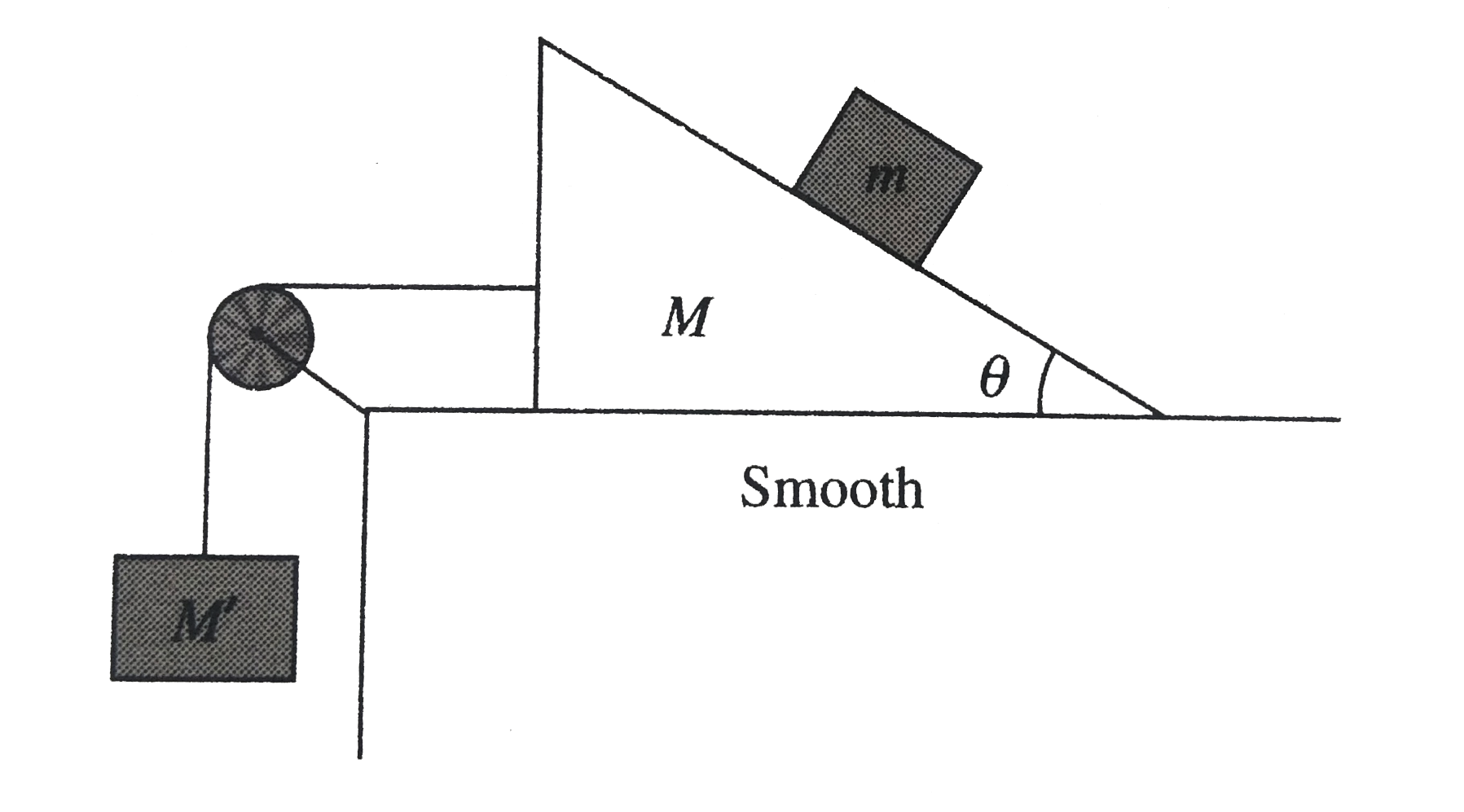 AThe value of M' is Mcotθ1−cotθBThe value of M' is Mtanθ1−tanθCThe value of tension in the string is MgtanθDThe value of tension is Mgcotθ
AThe value of M' is Mcotθ1−cotθBThe value of M' is Mtanθ1−tanθCThe value of tension in the string is MgtanθDThe value of tension is MgcotθA block of mass m is resting on an inclined plane. The inclination of the plane to the horizontal is gradually increased. It is found that when angle of inclination is θ, the block just begins to slide down the plane. What is the minimum force F applied parallel to the plane that would just make the block move up the plane?
A2mgsinθBmgsinθCmgcosθD2mgcosθ
Find out the minimum force that must be applied on the block vertically downwards so that the block doesn’t move.
View SolutionTwo block of masses m1 and m2 connected by a light spring rest on a horixontal plane. The cofficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
View SolutionWhat force should be applied on the wedge so that block over it does not move? (All surfaces are smooth)

View SolutionA block of mas M is resting on an inclined plane as shown in the figure. The inclination of the plane to the horizontal is gradually increased. It is found that when the angle of inclination is θ the block just begins to slide down the plane. What is the minimum force F applied parallel to the plane that would just make the block move up the plane ?
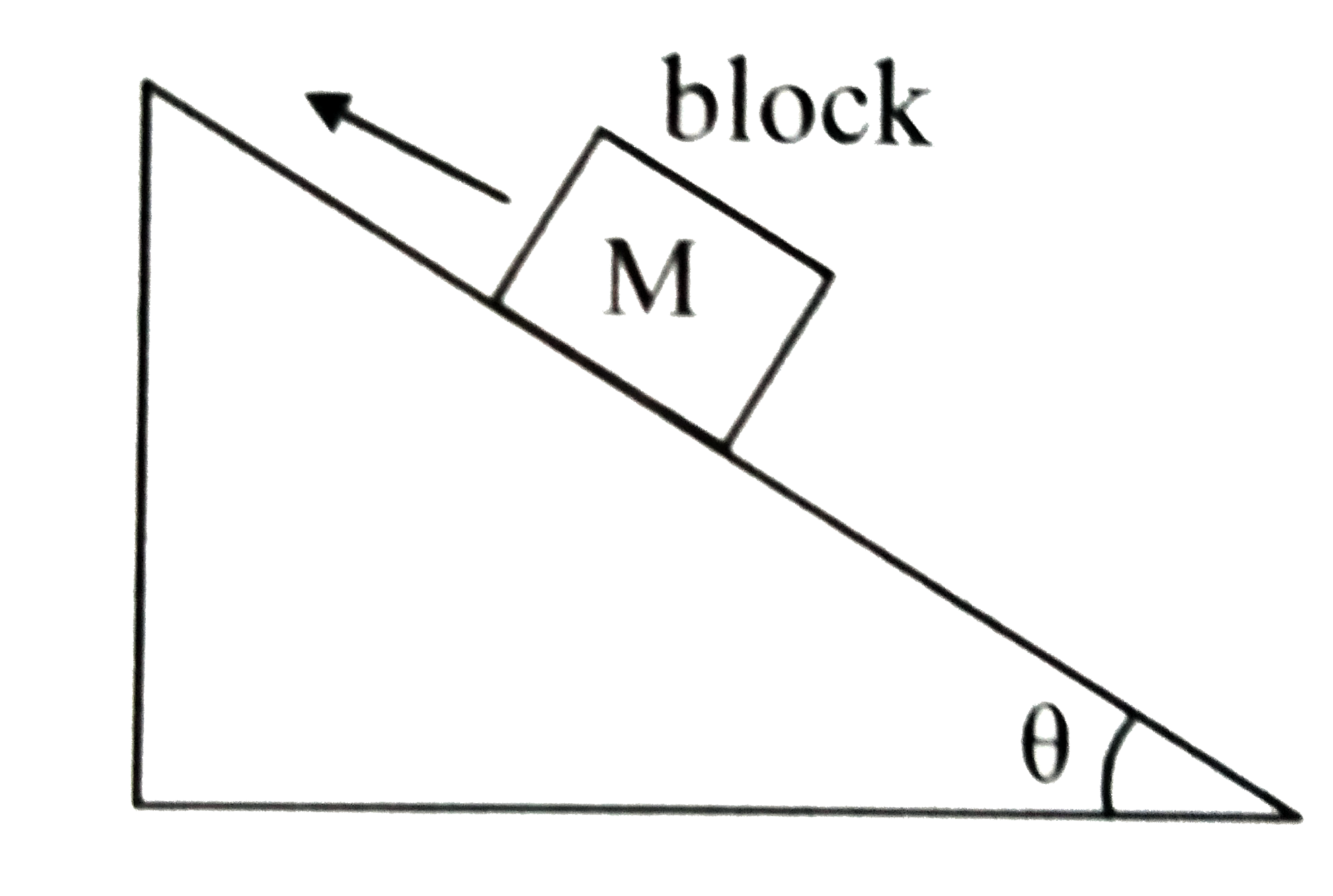
View SolutionA block of weight 1 N rests on a inclined plane of inclination θ with the horizontal. The coefficient of friction between the block and the inclined plane is μ. The minimum force that has to be applied parallel to the inclined plane to make the body just move up the plane is
View Solution