When a body slides down from rest along a smooth inclined plane making an angle of 30∘ with the horizontal, it takes time 20s. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it takes time 20p is, where p is some number greater than 1. The coefficient of friction between the body and the rough plane is
μ=(1−1p2)1√3
μ=(1−19p2)
μ=(1−p2)1√3
μ=√1−9p2
The correct Answer is:A
The acceleration of the body sliding down smooth inclined plane is a=g sinθ
The acceleration of the same body sliding down a rough inclined plane is
a'=gsingθ−μgcosθ=g(sinθ−μsinθ)....(ii)
As the body slides a distance d in each case,
∴d=12at2=12a't2(∴u=0)
∴aa'=t'2t2=p2(∴t'=20ps,t=20s)
gsinθg(sinθ−μcosθ)=p2(Using (i) and (ii))
sinθ=p2sinθ−μp2cosθ,μp2cosθ=p2sinθ−sinθ
μcosθ=(p2−1)p2sinθ,μ=tanθ(1−1p2
Here, θ=30∘∴μ,=((1−1p21√3
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - Circular Motion
14 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - Solving Problem In Mechanics
16 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - Equilibrium Of A Particle
6 Videos
- KINETIC THEORYBOOK - NCERT FINGERTIPSCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
When a body slides down from rest along a smooth inclined plane making an angle of 30∘ with the horizontal, it takes time T. When the same body slides down from the rest along a rough inclined plane making the same angle and through the same distance, it takes time aT, where a is a constant greater than 1. The co-efficient of friction between the body and the rough plane is 1√x(a2−1a2) where x = ________.
View SolutionWhen body slides down from rest along smooth inclined plane making angle of 45∘ with the horizontal, it takes time T When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance it is seen to take time pT, where p is some number greater that 1. Calculate late the coefficient of friction beween the body and the rough plane.
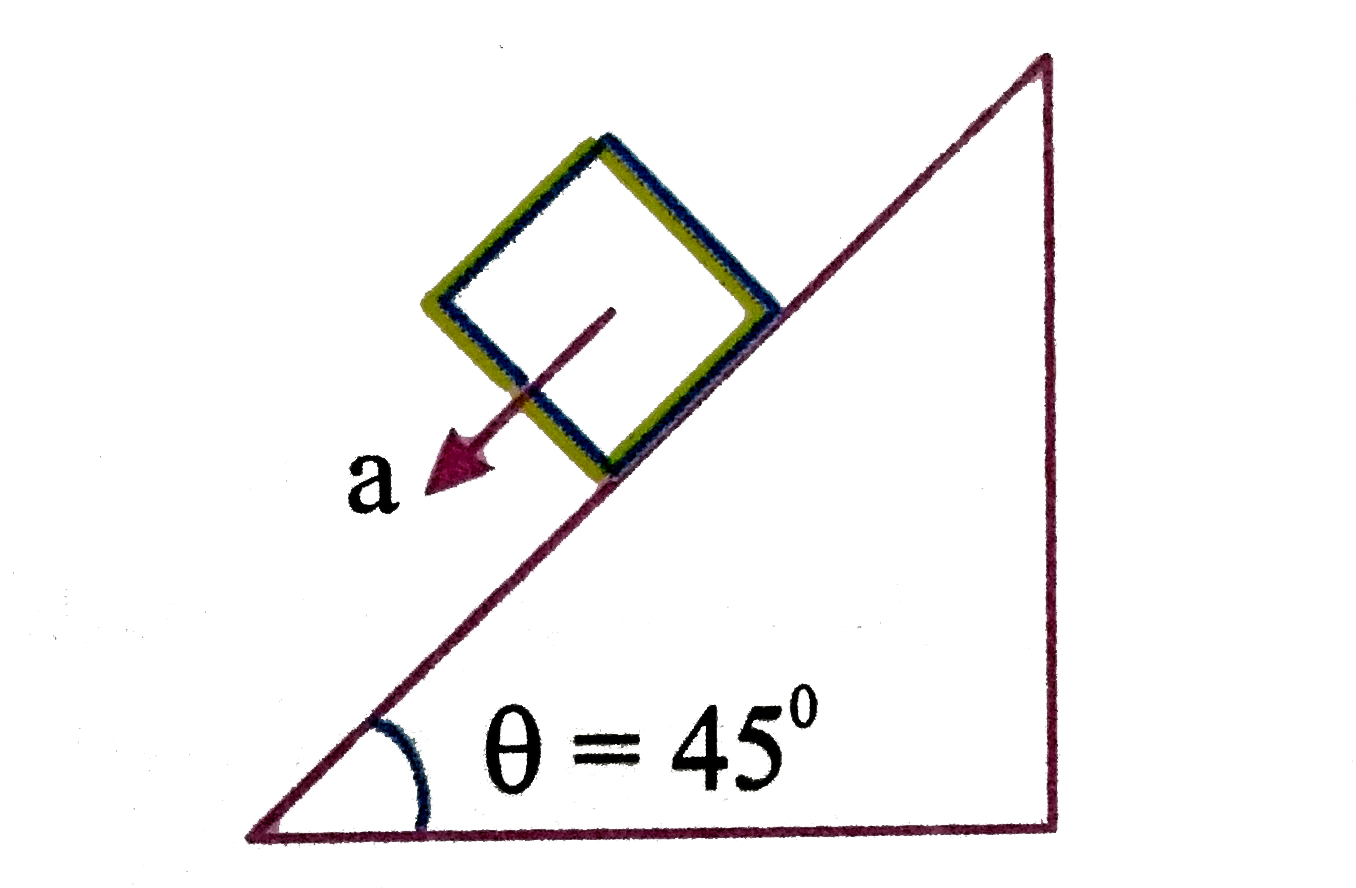 .
.
View Solution
Knowledge Check
When body slides down from rest along smooth inclined plane making angle of 45∘ with the horizontal, it takes time T When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance it is seen to take time pT, where p is some number greater that 1. Calculate late the coefficient of friction beween the body and the rough plane.
 .A(1−1P2)B(1+1P2)C1P2D−1P2
.A(1−1P2)B(1+1P2)C1P2D−1P2A body of mass m is launched up on a rough inclined plane making an angle 45∘ with horizontal If the time of descent between plane and body is
A25B35C34D45Starting from rest , a body slides down at 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is
A0.33B0.25C0.75D0.80
Derive an expression for the work done when a body slides down a rough inclined plane.
View SolutionA body is sliding down an inclined plane forming an angle 30∘ with the horizontal. If the coefficient of friction is 0.3 then acceleration of the body is
View SolutionAn object is placed on the surface of a smooth inclined plane of inclination θ. It takes time t to reach the bottom. If the same object is allowed to slide down a rough inclined plane of inclination θ, it takes time nt to reach the bottom where n is a number greater than 1. The coefficient of friction μ is given by:-
View SolutionA body is sliding down an inclined plane forming an angle 30∘ with the horizantal. If the coefficient of friction is0.3 then acceleration of the body is
View SolutionAn object is placed on the surface of a smooth inclined plane of inclination . It takes time t to reach the bottom of the inclined plane. If the same object is allowed to slide down rough inclined plane of same inclination , it takes time nt to reach the bottom where n is a number greater than 1. The coefficient of friction is given by -
View Solution
